ПрименПроизвИсследФ-й

Вариант 30

1. Доказать, что функция y = ex+ x2 + 2ex удовлетворяет уравнению y′− y = 2xex+ x2 .

2.Заменяя приращение функции дифференциалом, найти приближенное зна- чение выражений:

а) 4		;	б) lg11;	в) arctg	0,98	.
	258
					1,02

3.y = (1 + x2 )arctg x . Найти y′′ .

4.	Разложить функцию f (x) = xsin (x 2) по формуле Маклорена n -го по-
	рядка с остаточным членом в форме Пеано.
5.	Доказать неравенство arctg x ≤ x при x ³ 0.

6.Исследовать функции и построить их графики:

	а) f (x) =	(x −1)2			;		б)	f (x) = (1 − x) e2x−1;
		x2 − 2x
	в) f (x) =	x2		+ 1		;	г)	f (x) = 2cos x + sin 2x.
			x2	−1
	7. Для функции спроса						y = 5 x в зависимости от цены		x найти эластич-
	ность спроса по цене						Ex (y) в точках x =1,	x = 4, x = 8,	x = 10 . В каждом

из рассмотренных случаев выяснить, является ли спрос эластичным, ней- тральным или неэластичным.

8.Зависимость объема выпуска продукции Q от времени t определяется функцией Q = 100t + 13ln(32 + t3 ). Найти промежуток времени, в течение которого количество произведенной продукции увеличивается. С какого момента времени производство замедляется?

33

ПРИМЕРНЫЙ ТИПОВОЙ ВАРИАНТ

1. Доказать, что функция y = 3 tg (2x − 1) удовлетворяет уравнению

y′′ = 43 y y′ .

2.Найти время удвоения вклада в банк, если ставка банковского процента за год составляет 10 % годовых.

3.Заменяя приращение функции дифференциалом, найти приближенное значение выражений:

1) f (x)=		при x =1,03 ;	2) y = sin2 5x .
	x3 + 5x + 3

4.С какой относительной погрешностью надо измерить радиус шара, чтобы объем его можно было определить с точностью до 1 %?

5.Найти n-ю производную функций:

1) y =		x	;	2) y = sin2 5x .
		− x2
4

6.Разложить функцию f (x) = ln (1+ x) по формуле Тейлора в окрестности точки x0 = 2 .

7.Исследовать функции и начертить их графики:

		(x −1)3								2x
1)	y =		;			2)	y = 3 x2 e−			3	;
		3(x + 1)2
	f (x) = 2x − 33				;		f (x) = ln(x2 + 4x).
3)				(x −1)2		4)
8.	Доказать неравенство 1 + 2ln x≤ x2 при						x > 0.

9. В соответствии с прогнозами прибыль предприятия описывается функци-

ей π(q)= q2 − 8q + 10, где q – величина, характеризующая объем производства

(млн руб.). Найти оптимальный объем выпуска продукции, производимой фирмой.

34

10. В экономике цена обычно откладывается по вертикальной оси, а величи- на спроса по горизонтальной оси, уравнение спроса обычно записывается так, что цена p является функцией спроса q , а не q – функцией p . Рассмотрим

уравнение спроса: p = 940 - 48q + q2 . Какова эластичность спроса по цене при продаже 10 единиц продукции?

РЕШЕНИЕ ЗАДАЧ ТИПОВОГО ВАРИАНТА

Пример 1

Показать, что функция y = 3 tg (2x − 1) удовлетворяет уравнению

y¢¢ = 43 y y¢ .

Решение. Применяя правило дифференцирования производной сложной

функции, находим первую производную

y¢ =

3

(2x -1)¢ =

6

.

cos2 (2x -1)

cos2

(2x -1)

Еще раз дифференцируя y′ ,

получим

y′′ = 6 ×(- 2)cos−3 (2x -1)(- sin(2x -1))× 2 =

= 24sin(2x -1) = 24

tg (2x -1)

. Подставим y

и y′ в правую часть уравнения:

cos2 (2x -1)

cos3 (2x -1)

4

6

tg (2x −1)

¢¢

3 × 3tg(2x -1) cos2 (2x -1) = 24 cos2 (2x -1) º y

. Получаем тождество,

следова-

тельно, функция y удовлетворяет данному уравнению.

Пример 2

Найти время удвоения вклада в банк, если ставка банковского процента за год составляет 10 % годовых.

Решение. Найдем количество лет T , в течение которых сумма вклада уве-

		æ		10		ö
	личится в 2 раза. За год вклад увеличивается в	ç1	+			÷	=1,1 раз, поэтому за
				100
		è				ø
	T лет вклад увеличится в (1,1)T раз. Т.о.,	необходимо решить уравнение

35

(1,1)T = 2. Логарифмируя, получаем T ln1,1= ln 2 , откуда T =

ln 2

. Для прибли-

ln1,1

женного вычисления ln1,1 воспользуемся формулой

f

x0 +

x ≈ f

x0

+ f ' x0

x,

x → 0.

(1)

Полагая

f (x)= ln x , найдем

f '(x)=

1

и ln(x + Dx)» ln x +

x

.

В данном

x

x

примере при x =1 и

x = 0,1 получим ln1,1 ≈ 0,1. Т. к.

ln 2 ≈ 0,7 , то время уд-

воения вклада

T ≈ 7 (лет).

Пример 3

f (x)=

1) Вычислить приближенно

значение

функции

x3 + 5x + 3

при

x =1,03 .

x = 0,03. Тогда f (1)=

Решение. Принимаем x

=1,

13 + 5 ×1 + 3

= 3. Найдем

0

производную

f ¢(x)=

3x2 + 5

, далее f ¢(1)=

8

4

. Согласно формуле (1)

6 =

3

2

x3 + 5x + 3

» 3 +

4

получаем

1,033 + 5 ×1,03 + 3

× 0,03 = 3,04.

3

2) Найти приближенное значение 3

.

7,98

Решение.

Имеем

3

= 3

= 2 3 1 -

0,02

= 2 3 1 -

1

.

Здесь

7,98

8 - 0,02

400

8

f (x)= 3

,

f ¢(x)=

1

,

f (1)

=1,

f ¢(1)=

1

,

x0

=1,

Dx = -

1

,

и

согласно

x

3

3

3 x2

400

æ

1

æ

1

ö

ö

599

формуле (1) получаем 3

7,98 » 2ç1 +

ç

-

÷

÷

=1

»1,998.

3

400

600

è

è

ø

ø

Замечание. В этом пункте можно было положить x0 = 8, тогда

x = −0,02.

36

Пример 4

С какой относительной погрешностью надо измерить радиус шара, чтобы объем его можно было определить с точностью до 1 %?

	Решение. V = 4	3	πr3	. Нужно, чтобы	DV	» dV	£ 0,01. Имеем	dV	= 3 dr	,
					V			V
						V			r

значит, drr £ (13)× 0,01. Итак, радиус шара нужно измерить с точностью 1/3 %.

Пример 5

1.Найти n-ю производную функций:

а) y =		x	;	б) y = sin2 5x.
		- x2
4

Для нахождения n-й производной функции полезно в некоторых случаях функцию предварительно преобразовать, например, рациональную функцию разложить на сумму простейших дробей, понизить степень тригонометриче-

ской функции и т. д. Так в пункте

a представим заданную функцию в виде

суммы простейших дробей:

x

=

A

+

B

. Умножая обе части этого ра-

- x2

2

- x

2 + x

4

венства

на

знаменатель

левой

части,

приходим к

тождеству:

x ≡ A(2 + x)+ B(2 − x).

Последовательно

полагая

x = 2,

x = −2 ,

получим:

2A + 2B = 0,

A − B = 1.

Отсюда

A =

1 ,

B = -

1 .

Таким

образом,

2

2

x

1 æ

1

1

ö

1

æ

-1

× (-1)-

1

ö

=

ç

-

÷ . Находим y¢

=

ç

÷,

4 - x2

(2

+ x)2

2 è 2

- x

2

+ x

ø

2 èç (2 - x)2

ø÷

y¢¢ =

1

ç (-1)(- 2)

× (-1)2

-

1× 2 ÷

,

y¢¢¢ =

1

ç (-1)(- 2)(- 3)

× (-1)3

-

1× 2 ×3 ÷,K,

æ

ö

æ

ö

2 èç (2 - x)3

ø÷

2 èç

(2 - x)4

ø÷

(2 + x)3

(2 + x)4

y(n)		1	æ	(-1)(- 2)(- 3)K(- n)	× (-1)n -	1× 2 × 3Kn ö			n!((2 + x)n+1 - (2 - x)n+1)
	=		ç				÷	=			.
				n+1		n+1			n+1
		2	ç				÷
			è	(2 - x)		(2 + x)	ø		2 (4 - x2 )

37

В пункте

б представим функцию y = sin2 5x

в виде

y =

1 (1 - cos10x).

1

1 æ

æ

p öö

2

Первая производная

y¢ =

(sin 10x)

×10 = -

×10. Если y(n−1) =

2

2

çcos ç10x +

÷÷

è

è

2 øø

1 æ

æ

p

öö

= -

çcos

ç10x +

(n

-1)÷÷ ×10n−1,

то

согласно

принципу математической ин-

2

2

è

è

øø

(n) =

1

æ

æ

p

öö

10 n æ

æ

p

öö

дукции y

çsin

ç10x +

(n -1)÷÷

×10n−1 ×10 = -

çcos ç10x +

n÷÷ .

2

2

2

2

è

è

øø

è

è

øø

2.Для функции y(x)= (x3 + 5x - 6)e4x в точке x = 0 найти производную 10-го порядка.

Решение. Заданная функция представляет собой произведение двух функ- ций. В этом случае для нахождения n -й производной нужно применить фор-

мулу Лейбница

									n
					y(n) = (u(x)v(x))(n) = å Cnk (u(x))(n−k ) (v(x))(k ),
							k =0
где	Cnk				n!		n(n − 1)K(n − k + 1)		.
			=			=
				k !(n - k )!			1× 2Kk
		Для заданной функции в случае n =10 формула Лейбница принимает вид
y(10)(x)= å10 C k (e4x )(10−k )(x3 - 5x + 6)(k ) = C0 (e4x )(10)(x3										- 5x + 6)(0) +
			k =0		10				10
									- 5x + 6)(2) + C3 (e4x )(7)(x3		- 5x + 6)(3).
+ C1		(e4x )(9)(x3 - 5x + 6)(1) + C 2 (e4x )(8)(x3
10							10			10

Так как (x3 - 5x + 6)(4) = K = (x3 - 5x + 6)(10) = 0, все остальные слагаемые равны нулю. Находим производные:

(e4x )(10) = e4x × 410, (e4x )(9) = e4x × 49 , (e4x )(8) = e4x × 48 , (e4x )(7) = e4x × 47 ,

(x3 - 5x + 6)(1) = 3x2 - 5, (x3 - 5x + 6)(2) = 6x, (x3 - 5x + 6)(3) = 6.

38

Соответственно при x = 0 получаем

(x3 - 5x + 6)(0)

= 6, (x3 - 5x + 6)(1)

= -5, (x3 - 5x + 6)(2)

= 0,

x=0

x=0

x =0

(e4x )(10)

= 410 , (e4x )(9)

= 49 , (e4x )(8)

= 48 , (e4x )(7)

= 47 .

x=0

x=0

x=0

x=0

Таким образом,

y(10)(0)=1× 410 × 6 +10 × 49 ×

(- 5)+

10 × 9

× 48 × 0 +

10 × 9 ×8

× 47

× 6 = 304 × 47 =

= 4 980 736.

1× 2

1× 2 × 3

Пример 6

Разложить функцию f (x) = ln (1+ x) по формуле Тейлора в окрестности

точки x0 = 2 .

1

1

Решение. Имеем

f (2)= ln3,

f ¢(x)=

,

f ¢(2)=

,

1 + x

3

f ¢¢(x)= -

1

f ¢¢(2)= -

1

f ¢¢¢(x)=

1× 2

f ¢¢¢(2)=

1× 2

,

,

,

33

, … ,

(1 + x)2

32

(1+ x)3

f (n)(x)=

(-1)n−1(n -1)!,

f (n)(2)=

(-1)n−1(n -1)!,

(1 + x)n

3n

f (n+1)(x)=

(-1)n n!

,

f (n+1)(x)=

(-1)n n!

, где

2 < ξ < x .

(1+ x)n+1

(1+ x)n+1

1

1

2

1× 2

3

Поэтому

f (x) = ln 3 +

(x - 2) -

(x

- 2)

+

(x - 2) + ...+

1!×3

2!×32

3!×33

(-1)

n−1

(n -1)!

n

(-1)

k −1

(x

-

k

+

(x - 2)n + R

(x) = ln 3 + å

2)

+ R

(x),

k ×3k

n! 3n

n+1

k =1

n

+1

где Rn+1(x)=

(-1)n n!

(x -

2)n+1 =

(-1)n

(x - 2)n+1, 2 < ξ < x .

(1+ x)n+1(n +1)!

(1+ x)n+1(n + 1)

39

Пример 7

Исследовать функции и начертить их графики:

	y =	(x -1)3							e−	2x
1.			;				y = 3	x2
						2.				3	;
		3(x +1)2
	f (x) = 2x - 33				;		f (x) = ln(x2 + 4x).
3.				(x -1)2		4.
	y =	(x -1)3
1.			.
		3(x +1)2

Решение.

А) Область определения функции D(y)= (− ∞;−1)U (−1;+∞). Функция об-

ращается в ноль при x =1, при x = 0 y = -

1

, т. е. график функции пересекает

3

æ

0;-

1

ö

y < 0 , а

ось Ox в точке (1, 0), ось Oy в точке ç

3

÷. При x (− ∞; − 1)U (−1;1)

è

ø

при x (1;+ ∞)

y > 0 (рис. 1).

sgn y

-

-

+

x

-1

1

Рис. 1

Б)

Исследуем точку

разрыва

x = −1.

Так как пределы функции

при

x → −1 − 0

(слева)

и

при

x → −1 + 0

(справа) бесконечны,

т.

е.

lim

(x -1)3

= -¥ ,

lim

(x -1)3

= -¥ , то прямая x = −1 является верти-

x→−1−0 3(x +1)2

x→−1+0 3(x +1)2

кальной асимптотой.

Найдем наклонные асимптоты

y = kx + b :

k = lim

y

= lim

(x -1)3

=

1

,

x→∞ x

x→∞ 3x (x +1)2

3

40

b = lim (y - k x)=

1

æ

(x -1)3

ö

1

æ

- 5x2 + 2x -1

ö

5

lim

ç

- x÷

=

lim

ç

÷

= -

.

2

2

x→∞

x→∞ 3

ç

÷

x→∞ 3

ç

÷

3

è

(x + 1)

ø

è

(x +1)

ø

Итак, наклонная асимптота y = 13 x - 53 .

В) Определим промежутки монотонности и экстремумы данной функции.

Первая производная функции равна: y¢(x)= (x -1)2 (x + 5) . Находим критиче- 3(x + 1)3

ские точки: y′ = 0 при x = 1, x = −5 и y′ не существует при x = −1.

При x (− ∞; − 5)U (−1;1)U (1; + ∞)	y′ > 0 , при x (− 5;1)	y′ < 0 . На про-
межутках x (− ∞; − 5]U (−1;1]U [1; + ∞)	функция возрастает,	на промежутке

x [− 5;−1) убывает (рис. 2), в точке (-5; -4,5) имеет локальный минимум. От-

метим, что y′(1)= 0,	т. е. график функции имеет в этой точке горизонтальную
y′	+	-	+	+

у	-5	-1	1	х
		Рис. 2

касательную, точка x =1 является критической, но локального экстремума у функции в этой точке нет, т. к. первая производная не меняет знак.

Г) Определим промежутки выпуклости и точки перегиба графика

функции. Находим вторую производную функции: y¢¢(x)= 8 (x -1). Точки из

(x +1)4

области определения первой производной, в которых вторая производная обращается в нуль или не определена, являются точками возможного перегиба графика функции. В нашем случае это точка x =1. Так как y′′ > 0 при

x (1; + ∞), то на этом интервале график функции является выпуклым вниз.

Аналогично при x (− ∞; −1)U (−1;1) y′′ < 0 , т. е. на соответствующем интер-

вале график функции является выпуклым вверх. Следовательно, точка (1; 0) –

41

это точка перегиба графика функции (рис. 3).

y′′	-	-	+
у	Ç -1	Ç	1 È х

Рис. 3

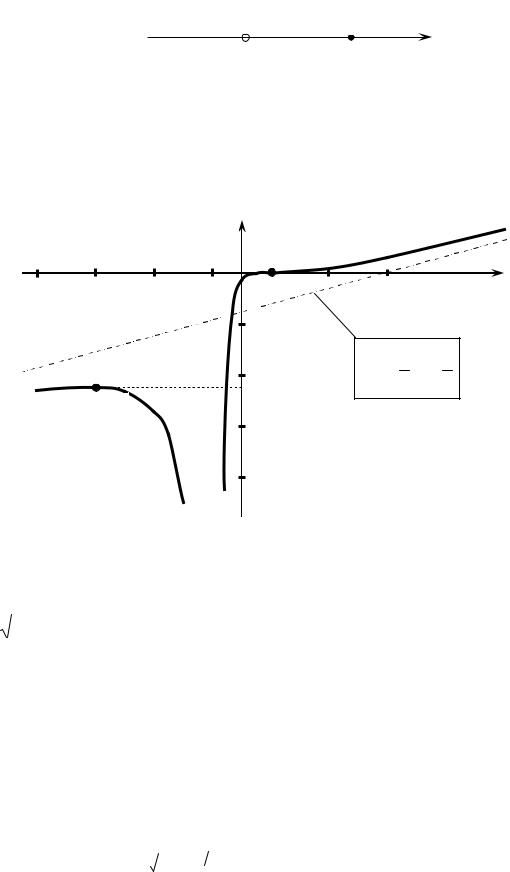
График данной функции, построенной по результатам исследования представ- лен на рис. 4.

у

(1; 0)

− 1	5	х
	− 2

y = 13 x − 53

(−5;−4,5)

Рис. 4

−

2x

2. y = 3 x2 e

3 .

Решение.

А)

Область определения функции D(y) = R ; y(x)³ 0 при x R , y(0)= 0.

Б)

Вертикальных асимптот нет, т. к. функция непрерывна при всех x R .

Найдем наклонные асимптоты

y = kx + b :

k

= lim

y(x)

=

lim

1

= 0;

+

× e2x 3

x→+∞

x

x→+∞ 3

x

42