ПрименПроизвИсследФ-й

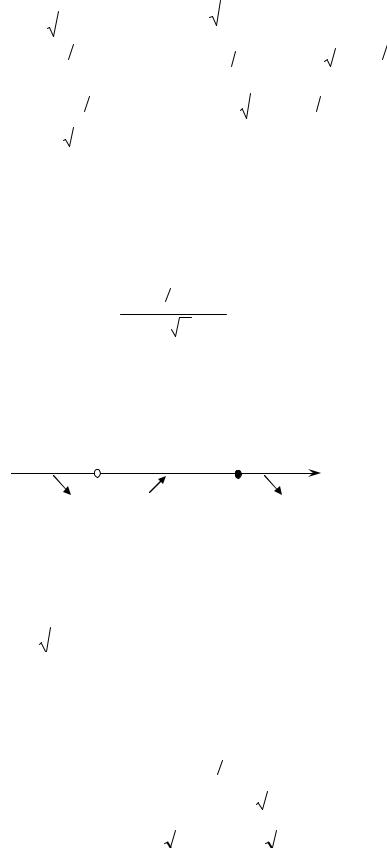
æ3

ö′

3

x

2

2

x

æ

¥ ö

ç

÷

1

b

lim

y(x)=

lim

lim

è

ø

lim

= 0 ;

=

= ç

÷ =

=

+

x→+∞

x→+∞ e2x 3

è

¥

ø

x→+∞ (e2x 3 )¢

x→+∞ 3

x

× e2x 3

y(x)

− 2x 3

3

e−2x 3

k

lim

lim

e

æ

¥ ö

= -2 lim

x2

= -¥ .

−

=

=

= ç

÷

x→−∞

x

x→+∞

3 x

è

¥ ø

x→+∞

1

Следовательно,

при x → +∞

имеем правую

горизонтальную асимптоту

y = 0; при x → −∞ наклонных и горизонтальных асимптот нет.

В) Определим промежутки монотонности и экстремумы данной функции.

Первая производная функции: y¢ = 2e− 2x 3 (1 - x). Находим критические точки: 3 3 x

y′ = 0 при x =1 и y′ не существует при x = 0. При x Î(- ¥; 0)U (1; + ¥) y′ < 0,

при x Î(0;1) y′ > 0 . На промежутках (- ¥; 0]U [1; + ¥) функция убывает,

y′ -	+		-
y	0	1	х

Рис. 5

на промежутке x Î[0;1] функция возрастает (рис. 5); локальный минимум (0; 0);

æ	3			ö	» (1; 0,51); в точке (0; 0) – вертикальная полука-
		e	−2
локальный максимум ç1;			÷
è			ø

сательная x = 0, y(x)³ 0 .

Г) Определим

промежутки

выпуклости

и точки

перегиба

графика

функции.

Вторая

производная

y¢¢(x)=

2e−2x 3 (2x2

- 4x -1)

.

Найдем корни

9 x 3

x

, x

уравнения

2x 2 − 4x − 1 = 0:

x

=1-

6

2

=1 +

6

(x ≈ −0,22; x

≈ 2,22).

1

2

2

1

2

Так как y′′ > 0 при x (− ∞; x )U

(x

2

; + ∞), то на этих интервалах график функ-

1

43

ции является выпуклым вниз. Аналогично при x

(x ; 0)U (0; x

2

)

y′′ < 0 , т. е.

1

на соответствующих интервалах график функции выпуклый вверх, рис. 6.

y′′

+

–

–

+

у

È х1

Ç 0

Ç х2

È х

Рис. 6

Точки

перегиба графика функции

(x1; y1 ),

(x2 ; y2 ).

Здесь

y1 = y(x1 )≈ 0,43,

y2 = y(x2 )≈ 0,39 . График функции представлен на рис. 7.

у

3

2

3 e-2 3

− 1

x1

1

2 х2

3

х

Рис. 7

3. y = 3 (x + 3) x2 .

Решение.

А)

Область определения

x R ;

y = 0

при

x = 0

и при

x = −3. При

x (− ∞; − 3) y < 0 , а при x (− 3; 0)U (0;+∞)

y > 0 . Точки (− 3; 0) и (0; 0) явля-

ются точками пересечения графика функции с осями координат.

44

Б) Вертикальных асимптот нет, так как функция определена и непрерывна

на множестве действительных чисел.

Для

наклонной асимптоты

y = k x + b

найдем коэффициенты:

3

k =

y

=

(x + 3)x2

=1; b =

lim (y − k x)= lim (3

− x) = 1,

lim

lim

(x + 3)x2

x→±∞ x

x→±∞

x

x→±∞

x→±∞

т. е. y = x + 1 – наклонная асимптота.

В)

Найдем производную y′(x)=

x + 2

; y′(x)= 0 при x = −2 и y′(x) не

3

(x + 3)2 x

существует при x = −3 и при x = 0.

y′	+	+	−	+
у		− 3	- 2	х
				0

Рис. 8

При x (− 2; 0) y′ < 0 , при x (− ∞; − 3)U (− 3; − 2)U (0;+∞) y′ > 0 . На проме-

жутке [− 2; 0] функция убывает, на промежутках (− ∞; − 3]U [− 3; − 2]U [0;+∞)

возрастает (рис. 8), в точке (−2; 34 ) имеет локальный максимум, в точке (0; 0)

локальный минимум. Отметим, что y'(− 2)= 0 , т. е. график функции имеет в

этой точке горизонтальную касательную. В точке (−3; 0) имеем вертикальную

y = 3

касательную x = −3 (функция

(x + 3) x2

в

точке

x = −3

непрерывна

и

lim

y'(x)= +∞).

Поскольку

y(x)

непрерывна

в

нуле

и

x→−3

lim

y′(x)= −∞,

lim

y′(x)= +∞; то полупрямая

x = 0,

y ³ 0

является и левой

x→0

−

x→0

+

и правой полукасательной к графику функции в точке (0; 0).Следовательно,

точка (0; 0) − точка возврата кривой.

Г) Определим промежутки выпуклости и точки перегиба графика функ-

45

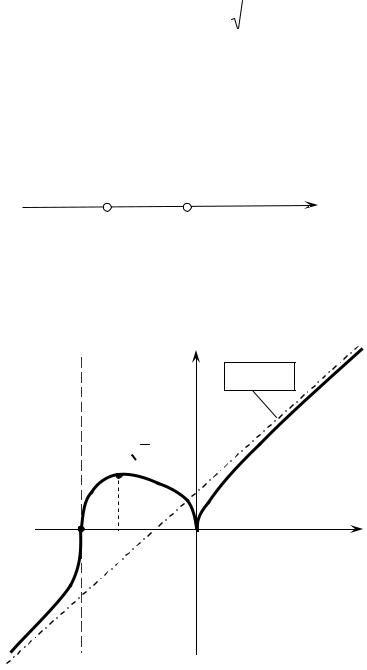
ции. Находим вторую производную		y¢¢(x)= -	2			. Знаки второй произ-
			3
				x4 (x + 3)5
водной: y′′(x)< 0	при x (− 3; 0)U (0; + ∞), y′′(x > 0) при					x (− ∞; − 3)	(рис. 9).
Точка перегиба	графика функции	(− 3; 0).	На промежутке (-¥;-3)				график

функции выпуклый вниз; на (− 3; 0) и (0; +¥) – выпуклый вверх.

y′′	+	-	-
y	È -3	Ç	0 Ç	х

Рис. 9 График данной функции представлен на рис. 10.

у

y =x+1

(−2;34)

−3 − 2

−1 0

х

Рис. 10

4. y = ln(x2 - 2x + 2).
Решение.
А)	Область определения x R . При	x =1 значение функции y = 0.
Б)	Вертикальных асимптот нет, т. к.	функция определена и непрерывна на

множестве действительных чисел. Для наклонной асимптоты y = kx + b найдем коэффициенты:

46

k =	lim	y		=	lim	ln (x 2 - 2 x + 2)	=	lim		2 x - 2	= 0;
		x				x			x 2	- 2 x + 2
	x → ±∞			x	→ ±∞		x	→ ±∞
	b = lim (y - k x)= lim ln (x2						- 2x + 2)= +¥ ,
			x→±∞			x→±∞

т. е. наклонных асимптот также нет.

	В)	Производная y¢ =		2x - 2			. Точка			x =1 является точкой минимума
			x2	- 2x +		2
функции; ymin = y(1)= 0.
				y¢¢ =	- 2x(x - 2)
	Г)	Вторая производная									. Знаки второй производной:
					(x2 - 2x + 2)2
′′	(x)< 0 при x (− ∞; 0)U (2; + ∞),					y		′′	(x)> 0	при x (0; 2). Точки перегиба
y

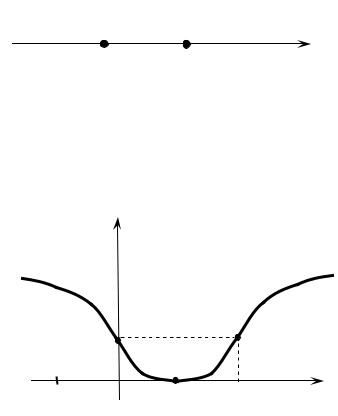
графика функции (2; ln 2) и (0; ln 2). При x (− ∞; 0)U (2; + ∞) график функции выпуклый вверх; на (0; 2) – выпуклый вниз (рис. 11).

y′′	-	+	-
у	Ç 0	È	2 Ç	х

Рис 11.

График данной функции представлен на рис. 12.

у

	ln2
− 1	0	1	2	х
		Рис. 12

47

Пример 8

		Доказать неравенство 1 + 2ln x£ x2 при					x > 0.
		Решение.			Рассмотрим	функцию f (x)= x2 - 2ln x -1. Имеем f (1)= 0,
f	¢	(x)=	2(x2	-1)	. При x > 1	′	0 < x < 1	′
			x			f (x) > 0, а при		f (x)< 0 . Таким образом,

f (x) на интервале (0; 1) убывает, на интервале (1; + ∞) возрастает, и т. к. функ-

ция f (x) непрерывна при x = 1, то точка x = 1 является точкой минимума. Сле-

довательно, при x > 0 f (x)= x2 - 2ln x -1³ f (1)= 0, откуда и вытекает неравен-

ство x2 ³1 + 2ln x, x > 0.

Пример 9

В соответствии с прогнозами прибыль предприятия описывается функ-

цией p(q)= q2 - 8q +10, где q – величина, характеризующая объем производ-

ства (млн руб.). Найти оптимальный объем выпуска продукции, производимой фирмой.

Решение. Предельная прибыль фирмы M π = ddqπ = 2q - 8. Приравниваем

производную нулю M π ≡ 2q − 8 = 0 → qextr = 4 . Является ли объем выпуска,

равный четырем,	оптимальным для фирмы? Исследуем характер изменения
знака производной. При q < qextr = 4 → π'(q)< 0 и прибыль убывает.
При q > qextr	= 4 → π'(q)> 0 и прибыль возрастает. Следовательно, в точ-
ке экстремума qextr	= 4 прибыль принимает минимальное значение, и, таким

образом, этот объем производства не является оптимальным для фирмы. Каким же будет оптимальный объем выпуска для фирмы? Ответ на этот

вопрос зависит от дополнительного исследования производственных мощно- стей фирмы. Если фирма не может производить за рассматриваемый период больше 8 единиц продукции ( π(q = 0)= π(q = 8)=10 ), то оптимальным реше-

48

нием для фирмы будет вообще ничего не производить, а получать доход от сда- чи в аренду помещений и/или оборудования. Если же фирма способна произво- дить за рассматриваемый период больше 8 единиц продукции, то оптималь-

ным решением для фирмы будет выпуск на пределе своих производственных мощностей.

Пример 10

В экономике цена обычно откладывается по вертикальной оси, а величи- на спроса по горизонтальной оси, уравнение спроса обычно записывается так,

что цена

p является функцией спроса q , а не

q – функцией

p . Рассмотрим

уравнение спроса:

p = 940 − 48q + q2 . Какова эластичность спроса по цене при

продаже 10 единиц продукции?

При

q = 10

цена

p = 940 − 480 + 100 = 560 ден. ед. Найдем производную

dq

=

1

=

1

.

При q = 10 получаем

dq

=

1

= -

1

. Поэто-

dp

dp

- 48 + 2q

dp

- 48 + 2 ×10

28

dq

му E p (q)= -

1

×

560

= -2 . Таким образом, изменение цены на

1 % от теку-

28

10

щей цены 560 ден. ед. изменит величину спроса в обратном направлении на 2 %. Мы приходим к выводу, что при цене 560 ден. ед. спрос эластичен.

49

Библиографический список

1.Виноградова И.А. Задачи и упражнения по математическому анализу: в

2 кн. / И.А. Виноградова, С.Н. Олехник, В.А. Садовничий. М.: Высш.

шк., 2000. Кн. 1. 725 с.

2. Общий	курс высшей математики для экономистов / В.И. Ермаков
[и др.].	М.: ИНФРА-М, 2000. 656 с.

3.Замков О.О. Математические методы в экономике / О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных. М.: ДИС, 1997. 368 с.

4. Колесников А.Н. Краткий курс математики для экономистов / А.Н. Колесников. М.: ИНФРА-М, 1997. 208 с.

5.Красс М.С. Основы математики и ее приложения в экономическом об- разовании / М.С. Красс, Б.П. Чупрынов. М.: Дело, 2001. 688 с.

6. Высшая математика для экономистов / Н.Ш. Кремер [и др.].

М.: ЮНИТИ, 1998. 472 с.

7.Практикум по высшей математике для экономистов / Н.Ш. Кремер

[и др.]. М.: ЮНИТИ-ДАНА, 2005. 423 с.

8.	Сборник	задач	и упражнений	по математическому	анализу /
	С.И. Ляшко [и др.]. М.: Изд. дом «Вильямс», 2001. Ч. 1. 432				с.
9.	Малыхин	В.И.	Математика в	экономике / В.И.	Малыхин.

М.: ИНФРА-М, 2001. 356 с.

10.Сборник задач по математике для втузов / под ред. А.В. Ефимова, Б.П. Демидовича. М.: Наука, 1986. Ч. 1. 464 с.

11.Томпсон А. Экономика фирмы / А. Томпсон, Д. Формби. М.: ЗАО «Изд-

во БИНОМ», 1998. 544 с.

12. Шикин Е.В. Математические методы и модели в экономике / Е.В. Шикин, А.Г. Чхартишвили. М.: Дело, 2000. 440 с.

50