Доказательство теоремы клапейрона

Определим работу, которую совершает сила , действующая, например, на балку, изображенную на рис. 15.1, а.

Будем считать, что нагрузка прикладывается к балке статически, то есть она медленно возрастает от нуля до заданной величины.

Пусть в некоторый момент сила, достигшая значения , вызвала в месте своего приложения прогиб балки, равный .

Увеличим это значение силы на бесконечно малую величину . Такое изменение нагрузки приведет к дополнительному прогибу . Очевидно, что элементарная дополнительная работа будет равна: .

Полная работа, совершенная внешней силой, определяется по формуле: 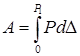.Для линейно деформируемой системы (график зависимости между прогибом и силой P для такой системы показан на рис. 15.1, б) прогиб балки пропорционален внешней нагрузке, то есть ,

где – коэффициент пропорциональности или перемещение от силы, равной единице . Коэффициент часто называют и податливостью системы.

Дифференцируя уравнение , найдем: .

Подставляя формулу в формулу 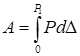и учитывая уравнение , получим: 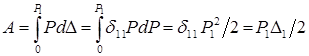,что и требовалось доказать. Полученное выражение соответствует теореме Клапейрона.

26. Теорема о взаимности работ (теорема Бетти).

Формулировка теоремы о взаимности работ (теоремы Бетти), доказанная в 1872 г Э. Бетти: возможная работа сил первого состояния на соответствующих перемещениях, вызванных силами второго состояния, равна возможной работе сил второго состояния на соответствующих перемещениях, вызванных силами первого состояния.

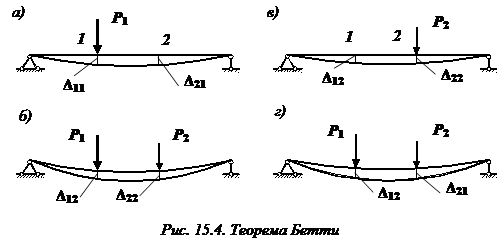
Доказательство теоремы о взаимности работ

Наметим на балке две точки 1 и 2 (рис. 15.4, а).

Приложим статически в точке 1 силу . Она вызовет в этой точке прогиб , а в точке 2 – .

Для обозначения перемещений мы используем два индекса. Первый индекс означает место перемещения, а второй – причину, вызывающую это перемещение. То есть, почти как на конверте письма, где мы указываем: куда и от кого.

Так, например, означает прогиб балки в точке 2 от нагрузки .

После того, как закончен рост силы . приложим в точке 2 к деформированному состоянию балки статическую силу (15.4, б). Балка получит дополнительные прогибы: в точке 1 и в точке 2.

Составим выражение для работы, которую совершают эти силы на соответствующих им перемещениях: .

Здесь первое и третье слагаемые представляют собой упругие работы сил и . Согласно теореме Клапейрона, они имеют коэффициент . У второго слагаемого этого коэффициента нет, поскольку сила своего значения не изменяет и совершает возможную работу на перемещении , вызванном другой силой .

Изменим теперь порядок нагружения балки. Сначала прикладываем к балке силу , а затем (рис. 15.4, в, г).

Тогда работа .

Очевидно, что . Из этого равенства следует теорема Бетти: .

Заметим, что теорема Бетти о взаимности работ справедлива как для случая внешних, так и для случая внутренних сил.

27. Теорема о взаимности перемещений (теорема Максвелла).

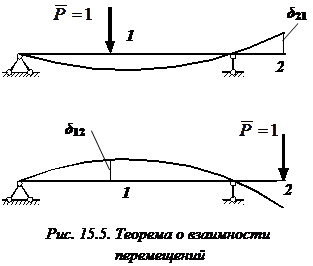
Пусть и . Теорема о взаимности перемещений с учетом принятого обозначения перемещения от единичной силы имеет вид: . Формулировка теоремы о взаимности перемещений: перемещение точки приложения первой единичной силы, вызванное действием второй силы, равно перемещению точки приложения второй единичной силы, вызванному действием первой единичной силы (рис. 15.5).