25.1. Метод максимального правдоподобия нахождения параметров распределения.

Метод предложен Р. Фишером в 1912 г. Метод основан на исследовании вероятности получения выборки наблюдений (x₁, x₂, …, x_n). Эта вероятность равна f(х₁, T) f(х₂, T) … f(х_п, T) dx₁ dx₂ … dx_n.

Совместная плотность вероятности

L(х₁, х₂ …, х_n ; T) = f(х₁, T) f(х₂, T) … f(х_n, T),

рассматриваемая как функция параметра T, называется функцией правдоподобия.

В качестве оценки q параметра T следует взять то значение, которое обращает функцию правдоподобия в максимум. Для нахождения оценки необходимо заменить в функции правдоподобия Т на q и решить уравнение δ L/δ q = 0. В целях упрощения вычислений переходят от функции правдоподобия к ее логарифму ln L. Такое преобразование допустимо, так как функция правдоподобия – положительная функция, и она достигает максимума в той же точке, что и ее логарифм. Если параметр распределения векторная величина q =(q ₁, q ₂, …, q _n), то оценки максимального правдоподобия находят из системы уравнений

δ ln L(q ₁, q ₂, …, q _n) / δ _q 1 = 0;

δ ln L(q ₁, q ₂, …, q _n) / δ _q 2 = 0;

. . . . . . . . .

δ ln L(q ₁, q ₂, …, q _n) / δ _q n = 0.

Для проверки того, что точка оптимума соответствует максимуму функции правдоподобия, необходимо найти вторую производную от этой функции. И если вторая производная в точке оптимума отрицательна, то найденные значения параметров максимизируют функцию.

Итак, нахождение оценок максимального правдоподобия включает следующие этапы: построение функции правдоподобия (ее натурального логарифма); дифференцирование функции по искомым параметрам и составление системы уравнений; решение системы уравнений для нахождения оценок; определение второй производной функции, проверку ее знака в точке оптимума первой производной и формирование выводов.

26.

26.1. Некоторые распределения связанные с нормальным распределением: Пирсона, Стьюдента.

Распределение χ² (хи-квадрат) с k степенями свободы— это распределение суммы квадратовkнезависимых стандартных нормальных случайных величин.

Пусть — совместно независимые стандартные нормальные случайные величины, то есть:.

Тогда случайная величина имеет распределение хи-квадрат сkстепенями свободы, обозначаемое; если же случайные величины связаны между собой одним линейным соотношением, например,то число степений свободы k = n – 1.

Распределение Стьюдентав теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений.

Пусть  — независимые стандартные нормальные случайные величины, такие что . Тогда распределение случайной величины , где

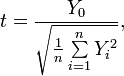
называется распределением Стьюдента с  степенями свободы. Пишут .

27.

27.1. Интервальные оценки параметров распределения.

Интервальный метод оценивания параметров распределения случайных величин заключается в определении интервала (а не единичного значения), в котором с заданной степенью достоверности будет заключено значение оцениваемого параметра. Интервальная оценка характеризуется двумя числами – концами интервала, внутри которого предположительно находится истинное значение параметра. Иначе говоря, вместо отдельной точки для оцениваемого параметра можно установить интервал значений, одна из точек которого является своего рода "лучшей" оценкой. Интервальные оценки являются более полными и надежными по сравнению с точечными, они применяются как для больших, так и для малых выборок. Совокупность методов определения промежутка, в котором лежит значение параметра Т, получила название методов интервального оценивания. К их числу принадлежит метод Неймана.

Постановка задачи интервальной оценки параметров заключается в следующем.

Имеется: выборка наблюдений (x₁, x₂, …, x_n) за случайной величиной Х. Объем выборки n фиксирован.

Необходимо с доверительной вероятностью g = 1– a определить интервал t₀ – t₁ (t₀ < t₁), который накрывает истинное значение неизвестного скалярного параметра Т (здесь, как и ранее, величина Т является постоянной, поэтому некорректно говорить, что значение Т попадает в заданный интервал).

Ограничения: выборка представительная, ее объем достаточен для оценки границ интервала.

Эта задача решается путем построения доверительного утверждения, которое состоит в том, что интервал от t₀ до t₁ накрывает истинное значение параметра Т с доверительной вероятностью не менее g . Величины t₀ и t₁ называются нижней и верхней доверительными границами (НДГ и ВДГ соответственно). Доверительные границы интервала выбирают так, чтобы выполнялось условие P(t₀ <= q <= t₁) = g . В инженерных задачах доверительную вероятность g назначают в пределах от 0,95 до 0,99. В доверительном утверждении считается, что статистики t₀ и t₁ являются случайными величинами и изменяются от выборки к выборке. Это означает, что доверительные границы определяются неоднозначно, существует бесконечное количество вариантов их установления.

На практике применяют два варианта задания доверительных границ: устанавливают симметрично относительно оценки параметра, т.е. t₀ = q – Еg , t₁ = q + Еg , где Еg выбирают так, чтобы выполнялось доверительное утверждение. Следовательно, величина абсолютной погрешности оценивания Еg равна половине доверительного интервала; устанавливают из условия равенства вероятностей выхода за верхнюю и нижнюю границу Р(Т > q + Е_1,g ) = Р(Т < q – Е_2,g )= a/2. В общем случае величина Е_1,g не равна Е_2,g . Для симметричных распределений случайного параметра q в целях минимизации величины интервала значения Е_1,g иЕ_2,g выбирают одинаковыми, следовательно, в таких случаях оба варианта эквивалентны.

Нахождение доверительных интервалов требует знания вида и параметров закона распределения случайной величины q . Для ряда практически важных случаев этот закон можно определить из теоретических соображений.

Метод позволяет по имеющейся случайной выборке построить функцию и(Т, q ), распределенную асимптотически нормально с нулевым математическим ожиданием и единичной дисперсией. В основе метода лежат следующие положения. Пусть: f(х, q ) – плотность распределения случайной величины Х; ln[L(x, q )] – логарифм функции правдоподобия;;

А² =М(у)² – дисперсия у. Если математическое ожидание М(у) = 0 и дисперсия у конечна, то распределение случайной величины w =  асимптотически нормально с параметрами 0 и 1 при  .