17.1. Теорема Пуассона.

Если число испытаний n в схеме независимых испытаний Бернулли стремится к бесконечности и  так, что np , , то при любых k = 0, 1, 2…

P_n(k) =

Это означает, что при больших nи малыхpвместо громоздких вычислений по точной формулеP_n(k) =p^kq^n-k можно воспользоваться приближенной формулой

P_n(k) = ,

т.е. использовать формулу Пуассона для λ = np.

На практике пуассоновским приближением пользуются при npq < 9.

18.

18.1. Характеристические функции и их свойства.

— мнимая единица,— вещественная переменная,— формула Эйлера,— способ вычисления математического ожидания комплекснозначной случайной величины, если математические ожидания её действительной () и мнимой () частей существуют.

Как всегда, модулем комплексного числаназывается число, так что.

Функциявещественной переменнойназываетсяхарактеристической функциейслучайной величины.

Свойства характеристической функции.

Свойство 1. Характеристическая функция всегда существует:

Свойство 2. По характеристической функции однозначно восстанавливается распределение (функция распределения, плотность или таблица распределения). Т.е. если две случайные величины имеют одинаковые характеристические функции, то и распределения этих величин совпадают.

Свойство 3. Характеристическая функция случайной величины  связана с характеристической функцией случайной величины  равенством:

Свойство 4.  Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых: если случайные величины  и  независимы, то, по свойству математических ожиданий

Свойство 5. Пусть существует момент порядка  случайной величины, т.е. . Тогда характеристическая функция  непрерывно дифференцируема  раз, и её -я производная в нуле связана с моментом порядка  равенством:

Свойство 6. Пусть существует момент порядка  случайной величины , т.е. . Тогда характеристическая функция  в окрестности точки  разлагается в ряд Тейлора

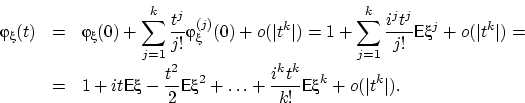
19.

19.1. Сходимость случайных величин и функций распределения.

20.

20.1. Центральная предельная теорема.

Центральные предельные теоремы— класс теорем, утверждающих, что сумма большого количества слабо зависимых случайных величин имеет распределение, близкое к нормальному. Так как многие случайные величины в приложениях являются суммами нескольких случайных факторов, центральные предельные теоремы обосновывают популярность нормального распределения.

Классическая формулировка центральной предельной теоремы.

ПустьX1, …,Xn, …есть бесконечная последовательность независимых одинаково распределенных случайных величин, имеющих конечное математическое ожидание и дисперсию.Обозначим последние черезμиσ²,соответственно. Пусть. Тогда

по распределению приn.

где N(0,1) – нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Обозначим черезX_Ввыборочное средние первыхnвеличин, то естьX_В=, мы можем переписать результат центральной предельной теоремы в следующем виде

по распределению приn.

21.