Analiticheskaya_Geometria

1.АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

1.1.Координаты точек на плоскости. Расстояние между двумя точками. Деление отрезка в данном отношении

Две взаимно перпендикулярные оси Ох и Оу, имеющие общее начало О и одинаковую масштабную единицу, образуют прямоугольную систему координат на плоскости.

Точка О называется началом координат; оси Ох и Оу − координатными осями, ось Ох − осью абсцисс, ось Оу − осью ординат. Оси Ох и Оу располагаются в координатной плоскости.

В	у	М
В		х
О	А	А

Пусть М − произвольная точка плоскости, МА и МВ − перпендикуляры, опущенные из точки М на оси Ох и Оу соответственно. Если величины отрезков ОА и ОВ равны А и В, то эти величины называются координатами точки М. Величина А называется абсциссой точки М, а величина В − ординатой. Если точка М имеет координаты А и В, то это символически обозначают М (А, В).

Теорема 1. Для любых двух точек M1(x1, y1 ) и M2 (x2 , y2 ) плоскости расстояние d между ними выражается формулой

d =

.

(1.1)

(x2 − x1 )2 + (y2 − y1 )2

Доказательство.

у

М2 (х2, у2)

х

О

М1 (х1, у1)

К (х2, у1)

По теореме Пифагора из треугольника М1М2К

M1M2

2 =

M1K

2 +

KM2

2 .

Учитывая, что

M1K

=

x2 − x1

,

KM2

=

y2 − y1

,

получим

M1M2

2 = (x2 − x1)2 +

+ (y2 − y1)2 или d =

. Теорема доказана.

(x2 − x1)2 + (y2 − y1)2

4

П р и м е р 1. Вычислить площадь правильного треугольника, если известны две его вершины А (6; -2) и В (-1; -4).

Решение. Как известно, площадь правильного треугольника вычисляется по формуле S = a243 , где а − сторона треугольника. В нашем случае

a = AB = (−1−6)2 + (−4 + 2)2 = 49 + 4 = 53 , поэтому искомая площадь треугольника S = 5343 (кв. ед.).

П р и м е р 2. Даны две смежные вершины квадрата А (4, −2) и В (5, 4). Вычислить площадь квадрата.

Решение. Площадь S квадрата находится по формуле S = a2 , где a − длина стороны квадрата. Поэтому для вычисления площади найдем длину

стороны AB: a = AB = (4 −5)2 + (− 2 − 4)2 = 37 . Таким образом,

S = a2 =37 (кв. ед.).

Теорема 2. Если точка М (х; у) делит отрезок М1М2 в отношении λ, считая от точки М1, то координаты этой точки определяются по формулам

	x =	x1 + λx2	,	y =	y1 + λy2	,	(1.2)
		1+ λ			1+ λ

где (х1; у1) и (х2; у2) − координаты точек М1 и М2 соответственно. Доказательство. Из точек М1, М, М2 опустим перпендикуляры на

ось Ох. Точки пересечения этих перпендикуляров с осью абсцисс обозначим Р1, Р и Р2 соответственно. Пусть М1К2 и МК перпендикулярны М2Р2,

К1 − точка пересечения М1К1 и МР.

		у		М2
		М
				К
М1				К2
			К1
				х
Р1	О	Р		Р2

Треугольники М1К1М и

МКМ2 подобны,

поэтому

=

M1M

= λ . Так как x2

x x1 ,

то

P1P

=

x − x1

= x − x1 ,

PP2

=

MM2

x − x1

= λ . Из последнего равенства следует, что

x =

x1 + λx2

.

x

− x

1+ λ

2

y1 + λy2

находим, что y =

. Теорема доказана.

1+ λ

P1P = M1K1 = PP2 K1K2

x2 − x = x2 − x и

Аналогично

5

Следствие. Если точка M(x, y) − середина отрезка, соединяющего точки M1(x1, y1 ) и M2 (x2 , y2 ) , то

	x =	x1 + x2	,	y =	y1 + y2	.	(1.3)
		2			2

Доказательство. Точка M(x, y) является серединой отрезка, соеди-

няющего точки M1(x1, y1 ) и M2 (x2 , y2 ), т. е. λ =1. Подставляя λ =1 в формулы (1.2), получим доказываемые равенства.

П р и м е р 3. Найти центр тяжести (точку пересечения медиан) треугольника, если заданы его вершины А (х1; у1), В (х2; у2) и С (х3; у3).

Решение. Пусть М(x4 , y4 ) − середина стороны АВ. Тогда x4 = x1 +2 x2 , y4 = y1 +2 y2 . В точке пересечения медианы делятся на отрезки в отношении 2:1, отчет ведется от вершины треугольника. Пусть O(x0 , y0 ) − точка пересечения медиан. Тогда OMCO = λ = 2 и по теореме о делении отрезка в данном

	отношении имеем: x0 =	x3 + 2x4	=	x1 + x2 + x3	,	y0 =	y3 + 2y4	=	y1 + y2 + y3	.
		3		3			3		3
	П р и м е р 4. Зная вершины A(1,−3) ,					B(2,0) и C(4,−6) параллелограмма

ABCD , найти координаты вершины D , противолежащей B .

Решение. Пусть в параллелограмме ABCD диагонали AC и BD пересекаются в точке O . По свойству параллелограмма его диагонали в точке пересечения делятся пополам, т. е. точка O является одновременно сере-

диной отрезков

AC и BD . По формуле (1.3) xO =

xA + xC

=

1+ 4

= 2,5, yO =

yA + yC

−3 −6

2

2

=

=

= −4,5. Так как точка O является серединой отрезка BD , то

2

2

xO =

xВ + xD

и yO =

yB + yD

. Из последних равенств находим:

xD = 2xO − xB =

2

2

= 5 − 2 = 3 ,

yD = 2yO − yB = −9 −0 = −9 . Таким образом, вершина D имеет коор-

динаты (3, −9) .

1.2. Вычисление площади треугольника через координаты вершин

Теорема 3. Пусть точки A(x1, y1) , B(x2 , y2 ) и C(x3, y3 ) являются вершинами треугольника. Тогда площадь этого треугольника может быть вычислена по формуле:

S =	1	mod		x1 − x2		y1	− y2		.	(1.4)
	2			x − x		y	− y
				1	3	1	3

Доказательство. Рассмотрим треугольник АВС, расположенный в плоскости Оху. Площадь этого треугольника равна разности площадей трапеции К1АВК2 и треугольников К1АС и СВК2.. Найдем площадь трапеции К1АВК2 и треугольников К1АС и СВК2:

6

SABK

K

= 1 (AK1 + BK2 ) K1K2

= 1 (y1 − y3 + y2 − y3 ) (x2 − x1 ),

2

1

2

2

SAK C = 1 AK1 K1C = 1 (y1 − y3 ) (x3 − x1 ),

1

2

2

SCK2 B =

1 CK2

BK2

= 1 (y2 − y3 ) (x2 − x3 ).

2

2

у

В (х2; у2)

А (х1; у1)

О

х

К1 (х1; у3)

С (х3; у3) К2 (х2; у3)

Таким

образом,

SABC =

1 ((y1 − y3 ) (x2 − x1) + (y2 − y3 ) (x2 − x1) −(y1 − y3 ) (x3 − x1) −

2

−(y − y ) (x − x )) =

1 ((y − y ) (x − x ) + (y − y ) (x − x ) −(y − y ) (x − x )) =

2

3

2

3

2

1

3

2

1

2

3

3

1

1

3

3

1

x1 − x2

y1 − y2

=

1

((y1 − y3 ) (x2 − x1) + (y2 − y1) (x3 − x1)) =

1

mod

.

2

2

x − x

y − y

1

3

1

3

Для любого другого расположения точек формула доказывается ана-

логично. Теорема доказана.

П р и м е р 5.

Вычислить площадь параллелограмма ABCD , если из-

вестны координаты его смежных вершин A(1,−3) ,

B (2,0)

и точки O (4,−6) пе-

ресечения его диагоналей.

Решение. Параллелограмм делится диагоналями на четыре равнове-

ликих

треугольника,

поэтому

SABCD = 4SABO .

Площадь

треугольника ABO

найдем по формуле (1.4): SABO =

1

mod

xA − xB

yA

− yB

=

1

mod

1− 2 −3 −0

=

2

x

− x

y

− y

2

1− 4

−3 + 6

A

O

A

O

=

1 mod

−1

−3 =

1

−3 −9 = 6 . Таким образом, SABCD = 4 6 = 24 (кв. ед.).

2

−3

3

2

П р и м е р 6.

Одна из вершин треугольника O находится в начале

координат, а вторая вершина A имеет координаты (−1, 6) . Найти координа-

ты третьей вершины B , находящейся на оси ординат,

если площадь тре-

угольника ABO равна 7 кв. ед.

Решение. Вершина B находится на оси ординат, поэтому ее абсцисса

равна нулю, т. е. точка

B имеет координаты (0, yB ) . Воспользуемся форму-

7

лой

(1.4)

для

нахождения

площади

треугольника,

получим:

SABO =

=

1

mod

xA

− xB

yA

− yB

=

1

mod

−1−0 6 − yB

=

1

mod

−1 6 − yB

=

1

yB

.

Так

2

x

− x

y

− y

2

−1−0 6 + 0

2

−1

6

2

A

A

O

O

как площадь треугольника ABO равна 7 кв. ед., относительно yB

получаем

уравнение

yB

=14 , т. е.

yB = ±14 . Таким образом,

вершина B имеет коор-

динаты (0,14)

или (0, −14) .

1.3. Уравнение прямой с угловым коэффициентом

Пусть дана некоторая прямая.

Определение. Углом α наклона данной прямой к оси Ox называется

угол, на который надо повернуть ось Ox , чтобы ее положительное направ-

ление совпало с одним из направлений прямой. Обычно в качестве угла α

берут наименьший положительный из данных углов.

Определение. Угловым коэффициентом прямой называется тангенс

ее угла наклона, т. е.

k = tgα .

(1.5)

у

y

M(x, y)

B

α

N

α

b

х

О

C

Если α = 0,

то прямая параллельна оси Ox . В случае α

=

π

прямая

параллельна оси Oy .

2

Выведем уравнение прямой, если известны ее угловой коэффициент

k и величина b , отсекаемая прямой на оси Oy (т. е. прямая не перпендику-

лярна оси Ox ).

MN = tgα .

Из треугольника

BMN :

Далее,

MN = CM − CN = CM −

BN

− OB = y −b , BN = CO = x . Таким образом,

y −b = k , или

y = kx +b .

x

(1.6)

Уравнение (1.6) называется уравнением прямой с угловым коэффи-

циентом k , отсекающей на оси Oy величину b . Если k = 0 , то уравнение

8

(1.6) принимает вид y = b и прямая, задаваемая этим уравнением, парал-

лельна оси Ox .

Любая прямая, не параллельная оси Oy , задается уравнением вида

(1.6), и любое уравнение вида (1.6) определяет прямую, не параллельную оси Oy .

1.4. Уравнение прямой, проходящей через данную точку

Выведем уравнение прямой, проходящей через точку M1(x1; y1) , с уг-

ловым коэффициентом k .

Прямая с заданным угловым коэффициентом имеет уравнение y = kx +b , в котором величина b неизвестна. Прямая проходит через точку

M1 ,	поэтому координаты этой точки удовлетворяют уравнению прямой,
т. е.	y1 = kx1 +b или b = y1 − kx1 . Следовательно, искомое уравнение имеет вид
y = k(x − x1) + y1 или
	y − y1 = k(x − x1 ) .	(1.7)

Замечание. Если прямая проходит через точку M1(x1; y1) параллельно оси Oy , то ее уравнение имеет вид x − x1 = 0.

Выведем уравнение прямой, проходящей через две заданные точки M1(x1; y1) и M2 (x2; y2 ) . Запишем уравнение прямой в виде (1.7):

y − y1 = k(x − x1) , где k − неизвестный коэффициент. Искомая прямая проходит через точку M2 (x2; y2 ) , поэтому выполняется равенство y2 − y1 = k(x2 − x1) .

Если

x1 = x2 ,

то искомая прямая параллельна оси

Oy и имеет вид

x = x1 .

Если

x1 ≠ x2 ,

то k =

y2 − y1

и

уравнение

(1.7)

принимает вид

x

− x

y2 − y1

2

1

y − y1 =

(x − x1) . В случае y1

= y2

прямая параллельна оси Ox и задается

x − x

2

1

уравнением

y = y1 .

Если же y1 ≠ y2 ,

уравнение прямой, проходящей через

две заданные точки, имеет вид

y − y1

=

x − x1

.

(1.8)

y

− y

x

− x

П р и м е р 7.

2

1

2

1

Составить уравнение прямой, проходящей через точку

M (−1, 8) и составляющей с осью абсцисс угол α = π .

Решение. По

3

формуле

(1.5)

угловой

коэффициент прямой

k = tg π3 = 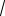3 . Согласно формуле (1.7) искомое уравнение прямой имеет вид

y −8 = 3(x +1) или 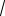3x − y +8 + 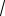3 = 0 .

П р и м е р 8. Составить уравнения сторон треугольника, вершины которого находятся в точках A(1,−3) , B (2, 3) и С (4,−2) .

Решение. Для того чтобы составить уравнения сторон указанного треугольника, воспользуемся формулой (1.8) уравнения прямой, проходя-

9

щей через две точки с различными абсциссами и ординатами. Сторона AB

задается уравнением

y +3

=

x −1

, или 6x − y −9 = 0 . Для стороны

BC урав-

3 +3

2 −1

нение имеет вид

y −3

=

x − 2

, или 5x + 2y −16 = 0 . Уравнение третьей сто-

− 2 −3

4 − 2

роны AC :

y +3

=

x −1

, т. е.

x −3y −10 = 0 .

− 2 +3

4 −1

1.5. Угол между двумя прямыми

Рассмотрим две прямые I и II, задаваемые уравнениями y = k1x +b1 и y = k2 x +b2 и образующие c осью Ox углы α1 и α2 соответственно.

y

I	ϕ	II
			x
α1		α2
	O

Тогда k1 = tgα1 , k2 = tgα2 . Угол α2 является внешним углом треугольника, образованного осью Ox и прямыми I и II. Пусть ϕ − один из углов между прямыми. Тогда α2 =α1 +ϕ или ϕ =α2 −α1 . Следовательно,

tgϕ = tg(α2 −α1) =	tgα2 −tgα1			=		k2 − k1		.					(1.9)
	1+tgα	2	tgα		1+ k k
			1		1		2			k1 − k2
Второй угол ϕ1 между прямыми равен π −ϕ							и tgϕ1 =						. За угол
									1		+ k k
											1	2

между прямыми принимается наименьший неотрицательный угол из углов

ϕ и ϕ1 .
Если две прямые параллельны, то tgϕ = tgϕ1 = 0 , поэтому k1	= k2 . Ус-
ловие	(1.10)
k1 = k2

является условием параллельности двух прямых. Если же прямые перпен-

дикулярны, то		угол ϕ =		π ,	α2 =α1	+	π	, следовательно,	tgα2 =
	+ π ) = −ctgα1 = −	1		2			2
tg(α1			или
	2	tgα
		1		k1k2 = −1.					(1.11)
	Это равенство является условием перпендикулярности двух прямых

сугловыми коэффициентами k1 и k2 .

Пр и м е р 9. Найти угол между стороной BC треугольника ABC и медианой, проведенной из вершины A, если A(1,−3) , B (2,10) и С (4,−2) .

10

Решение. Пусть точка M(x0 , y0 ) является серединой стороны BC , то-

гда по формуле (1.3) x0

=

2 + 4

= 3,

y0

=

10 − 2

= 4 . Составим уравнение сто-

2

2

y −10

x − 2

роны BC , воспользовавшись

формулой

(1.8);

=

, или

− 2 −10

4 − 2

y = −6x + 22 . Угловой коэффициент k1 прямой, содержащей сторону BC , ра-

вен

−6 . Медиана

AM

задается уравнением

y +3

=

x −1

.

Это уравнение

4 +3

3 −1

приводится к виду y =

7 x −

13 . Поэтому угловой коэффициент k2 прямой,

2

2

содержащей медиану AM , равен 7 . По формуле (1.9) тангенсы углов меж-

2

7

ду

стороной

BC

и

медианой

AM :

tgϕ =

k2 − k1

=

2 + 6

= −19 ,

1+ k k

1− 21

40

k1 − k2

= 19 .

1

2

tgϕ1

=

Учитывая, что за угол между прямыми

принимается

1+ k k

40

1

2

наименьший положительный из углов ϕ

и ϕ1 , получаем, что угол между

стороной BC и медианой AM равен arctg

19 .

40

Замечание. Угловой коэффициент k прямой,

проходящей через две

заданные точки M1(x1; y1) и M2 (x2; y2 ) с различными абсциссами, согласно (1.7) должен удовлетворять соотношению y2 − y1 = k(x2 − x1) . Если x1 ≠ x2 , то

k = y2 − y1 . x2 − x1

П р и м е р 10. Составить уравнение высоты, проведенной из вершины А на сторону BC , если A(1,−3) , B (2,10) и С (4,−2) .

Решение. Прямая, содержащая сторону BC , проходит через точку B , поэтому ее уравнение имеет вид (1. 7): y −10 = k(x − 2) . Угловой коэффици-

ент k этой прямой k1 = −42−−210 = −6 . Угловой коэффициент k2 высоты, про-

веденной из вершины A, находим из условия (1.11), т. е. k2 = 16 . Восполь-

зовавшись формулой (1. 7), получим искомое уравнение: y +3 = 16 (x −1) .

1.6. Общее уравнение прямой. Неполное уравнение первой степени. Уравнение прямой в отрезках

Теорема 4. В прямоугольной системе координат любая прямая задается уравнением первой степени

Ax + By +C = 0,

(1.12)

и уравнение (1.8) при любых коэффициентах A, B и C (при условии, что коэффициенты A и B одновременно не обращаются в ноль, т. е.

11

A2 + B2 ≠ 0 ) определяет некоторую прямую в прямоугольной системе координат Oxy .

Доказательство. Если прямая не перпендикулярна оси Ox , то она задается уравнением y = kx +b или kx − y +b = 0 . Введем обозначения A = k ,

B = −1, C = b и получим уравнение Ax + By +C = 0. Если прямая перпенди-

кулярна оси Ox , то все ее точки имеют одинаковые абсциссы, т. е. x = a . В этом уравнении A =1, B = 0 , C = −a .

Пусть дано уравнение Ax + By +C = 0. Если B ≠ 0 , то y = − BAx − CB , по-

ложив k = − BA, b = −CB , получим уравнение прямой, не перпендикулярной

оси Ox . Если B = 0 , то Ax +C = 0 и x = −CA , т. е. a = −CA и x = a − уравнение

прямой, перпендикулярной оси Ox . Теорема доказана. Уравнение (1.12) называется общим уравнением прямой.

Выведем уравнение прямой в отрезках. Пусть A ≠ 0 , B ≠ 0 и C ≠ 0 .

Тогда из уравнения (1.8): Ax + By = −C , или						Ax	+	By	=1. Обозначим a = −C ,
								−C
	= −C , получим					−C			A
b
	B
		x	+	y	=1.				(1.13)
		a
				b
	Уравнение (1.13) называется уравнением прямой в отрезках. Числа a
и b равны величинам отрезков,			которые прямая отсекает на осях Ox и Oy

соответственно.

Уравнение (1.12) является неполным уравнением прямой, если ка- кой-либо из коэффициентов A, B или C равен нулю. Возможны следующие случаи:

a) C = 0 ; уравнение Ax + By = 0 определяет прямую, проходящую через начало координат;

b) B = 0 ; x = −CA

Ox отрезок величины c) A = 0 ; y = −CB

Oy отрезок величины

П р и м е р 11 .

координатных осях, а

− прямая, параллельная оси Oy и отсекающая на оси

a = −CA ;

− прямая, параллельная оси Ox и отсекающая на оси

b = −CB .

Найти площадь ромба, диагонали которого лежат на одна из сторон задается уравнением 3x −7 y + 21 = 0 .

Решение. Ромб делится своими диагоналями на четыре равновеликих прямоугольных треугольника. Пусть прямая 3x −7 y + 21 = 0 пересекает оси

абсцисс и ординат в точках A и B соответственно. Площадь ромба равна

12

	4SABO . Уравнение стороны AB в отрезках имеет вид:	3x		+	7 y	=1 или
		− 21			21

−x7 + 3y =1. Таким образом, прямая AB отсекает на координатных осях от-

резки длиной 7 и 3 ед. Следовательно, SABO = 12 7 3 = 212 , а площадь ромба равна 42 (кв. ед.).

1.7. Расстояние от точки до прямой на плоскости

Рассмотрим прямую L на плоскости Oxy . Пусть прямая L задается

уравнением Ax + By +C = 0, причем	A2 + B2 ≠ 0 . В этом случае угловой ко-
эффициент k1 этой прямой равен −	A	. Проведем через точку	M0 (x0 , y0 ) пря-
	B

мую, перпендикулярную L и пересекающую ее в некоторой точке P(x1, y1) .

L	M0	(x0 , y0 )

P(x1, y1)

Уравнение прямой MP имеет вид Bx − Ay = Bx0 − Ay0 . Точка P являет-

ся пересечением прямых L и MP , поэтому ее координаты x1

и y1 должны

удовлетворять системе уравнений:

Ax

+ By

= −C,

(1.14)

1

1

− Bx1 + Ay1 = −Bx0 + Ay0.

Определитель этой системы A2 + B2

≠ 0 , поэтому по теореме Крамера

она имеет единственное решение:

=

− AC − By0 (A− B)

,

x1

2

+ B

2

A

− BC + Ax0 (A− B) .

y

=

1

2

+ B

2

A

A(Ax0 + By0

+C)

B(Ax0 + By0 +C)

Тогда x1 − x0

= −

, y1 − y0 = −

. По формуле

A2

+ B2

A2 + B2

Ax0 + By0 +C

(1.1) найдем длину отрезка M0P :

.

M0P

=

(x1 − x0 )2 + (y1 − y0 )2

=

A2 + B2

Дина отрезка M0P равна расстоянию d от точки M0 (x0 , y0 )									до прямой, зада-
ваемой полным уравнением Ax + By +C = 0, т. е.
d =			Ax0 + By0 +C					.	(1.15)
				A2 + B2
13