1.8 Контрольные вопросы

1Какие измерения называются прямыми?

2Какие результаты наблюдений относятся к равнорассеянным?

3Приведите алгоритм обработки исправленных результатов прямых равнорассеянных измерений.

4Как находится точечная оценка математического ожидания измеряемой величины?

5Что такое случайное отклонение результата наблюдений?

6Как определяется оценка с.к.о. результатов наблюдений?

7Какие критерии, используемые для определения грубых погрешностей, Вы знаете?

8Как находится оценка с.к.о. результата измерения?

9Как производится проверка нормальности распределения результатов наблюдений по составному критерию?

10Что такое коэффициент Стьюдента и как он находится?

11По какой формуле определяются доверительные границы случайной погрешности измерений?

12

2 ЛАБОРАТОРНАЯ РАБОТА ТМ.2 «ПРЕДВАРИТЕЛЬНАЯ

СОВМЕСТНАЯ ОБРАБОТКА НЕСКОЛЬКИХ РЯДОВ НАБЛЮДЕНИЙ

2.1 Цель работы

2.1.1Изучение метода и алгоритма предварительной совместной обработки нескольких рядов наблюдений.

2.1.2Приобретение практических навыков работы на персональном компьютере при предварительной совместной обработке нескольких рядов наблюдений.

2.2 Краткие сведения из теории Если многократные наблюдения проводятся в течение длительного периода

времени, необходимо учитывать, что изменение параметров средств измерений

ивнешней среды может вызвать систематические или случайные изменения математических ожиданий и с.к.о. результатов наблюдений. Для того чтобы эти изменения не ускользнули от внимания оператора, измерения производятся часто в несколько серий, причем перед каждой серией измерений иногда заново настраивают измерительную аппаратуру и принимают меры к стабилизации параметров внешней среды.

В этом случае получаем m групп по nj (j = 1,…, m) результатов наблюдений в каждой. Группы наблюдений будут равнорассеянными, если средние ариф-

метические x j и оценки с.к.о. σ~ x j во всех группах являются оценками одного и

того же истинного значения измеряемой величины и одного и того же с.к.о. Равнорассеянность групп наблюдений проверяется методами математиче-

ской статистики, известными под общим названием дисперсионного анализа. Предположим, что все N результатов наблюдений равнорассеяны. Тогда

M[xij] = M[x]

и

σ[xij] = σ[x],

где xij – i-й результат наблюдения в j-й группе.

Вычислим групповые средние арифметические x j и общее среднее x :

x j =

1

n j

xij;

j =1,...,m ;

1

m x

1

m

1

n j

.

(2.1)

x =

=

x

n j ∑

m

j

m

∑n j ∑

ij

∑

i=1

j=1

j=1

i=1

Очевидно, что для каждого xij имеет место тождество

xij − x = (x j − x) + (xij − x j) .

Возведем в квадрат обе его части и просуммируем их по всем i и j:

m n j

m

n j

m n j

m

n j

∑∑(xij −x)2 = ∑∑(x j −x)2 +∑∑(xij −x j )2

+2∑∑(x j −x)(xij −x j )=

j=1 i=1

j=1 i=1

j=1 i=1

j=1 i=1

13

m	m n j	m	n j
= ∑(x j − x)2	+ ∑∑(xij − x j )2	+ 2∑ (x j − x) ∑(xij − x) ,
j=1	j=1 i=1	j=1	i=1

Но сумма

Поэтому

n j
∑(xij − x j )= 0	по определению x j			для всех j.
i=1
m n j		m	m	n j
∑∑(xij −x)2		= ∑(x j −x)2	+∑∑(xij −x j )2		(2.2)
j=1 i=1		j=1	j=1 i=1

т.е. сумма квадратов отклонений результатов наблюдений от общего среднего равна сумме квадратов отклонений групповых средних от общего среднего и сумме квадратов отклонений результатов наблюдений от групповых средних.

Из равенства (2.2) можно получить следующие оценки с.к.о. результатов наблюдений:

~

1

m

n j

2

σI =

∑ ∑(xij − x)

;

(2.3)

N −1

j=1 i=1

~

1

m

2

σII

=

∑(x j − x)

;

(2.4)

m

−1 j=1

~

1

n j

2

σхj

=

∑(xij − x j )

;

j =1,K,m ;

(2.5)

n j −1i=1

~

1

m n j

2

1

m

~

2

σ

III

=

∑∑

(xij

−

x j )

=

∑(n j

−

1)

хj

,

(2.6)

N − m

N

− m

σ

j=1i=1

j=1

где ~ I с.к.о., характеризующее общее рассеивание в ряде наблюдений;

σ −

~

σ~II − с.к.о., характеризующее рассеивание между групповыми средними; σхj − с.к.о., характеризующее рассеивание внутри каждой j-й группы;

σ~III − с.к.о., характеризующее среднее рассеивание внутри групп;

m

N = ∑n j .

j=1

Для проверки гипотезы о равнорассеянности наблюдений используется распределение, которое получается следующим образом: если U и V - две незави-

симые случайные величины, подчиняющиеся χ2 - распределению с kδ и kм

(причем ~δ ~м) степенями свободы соответственно, то их отношение

σ > σ

14

	F	=	kмU		(2.7)
			kδV
	kδkм
	имеет F-распределение Фишера		с kδ и kм степенями		свободы
	(kδ =nδ−1; kм=nм−1).

F-распределению Фишера подчиняется распределение отношения двух не-

~		2		~2				и nм
зависимых оценок дисперсии σδ			и σм, вычисленных на основании nδ
нормально распределенных результатов наблюдений, т.е. отношение
~ 2			(n	м	−1) χ2
	σδ	=				n δ −1		(2.8)
~ 2				δ −		2
	σм		(n			1) χn м −1
имеет F– распределение с (nδ −1),		(nм −1) степенями свободы.

Значение F при различных значениях kδ =nδ −1; kм =nм −1 и уровнях значи-

мости q приведены в таблице И.1 методического пособия [2].
Если при выбранном уровне значимости q окажется, что
~2	~2	(2.9)
σδ /	σм < (Fnδ−1,nм−1)q ,
~2 ~2

где σδ > σм, то говорят, что различие оценок незначимо, и они являются двумя

независимыми оценками одной и той же дисперсии. В противном случае приходится признать это различие существенным, имеющим более глубокие причины, нежели просто расхождения, вызванные ограниченностью опытных данных.

Гипотезу о равнорассеянности групп результатов наблюдений проверяют в два этапа:

1 Вначале проверяется гипотеза о незначимости различий дисперсий ~2 во

σj

всех m группах наблюдений. Для этого их располагают в вариационный ряд в

порядке			~2	~2	и проверяют значимость отношения
		возрастания σmin		,...,σmax
~2	~	2	. Если это отношение незначимо, то незначимы и все остальные.
σmax / σmin

Тогда следует принять исследуемую гипотезу как правдоподобную и считать, что рассеяние результатов наблюдений относительно средних во всех группах одинаково. В противном случае приходится признать распределения в группах

~ 2	~ 2	отличными друг от друга и проверить значимость
с дисперсиями σmin	и σmax

отношений всех других дисперсий.

2 При незначимости различий дисперсий в группах проверяется гипотеза о незначимости различий математических ожиданий во всех группах наблюде-

ний. Если эта гипотеза верна, то ~2 и ~2 являются независимыми точечными

σII σIII

оценками одной и той же дисперсии и их отношение должно починяться F– распределению с m –1 и N – m степенями свободы. Если расхождение оценок значимо при выбранном уровне значимости, то приходится признать, что при проведении измерений имели место случайные или систематические сдвиги ре-

15

зультатов наблюдений, вследствие чего расхождения между средними оказались больше тех, которые могут быть оправданы ограниченностью опытных данных.

При небольшом количестве групп наблюдений можно для всех комбинаций

серий измерений (обозначим их индексы через с и d) вычислить величины tc-d и использовать их для проверки гипотезы о равенстве математических ожиданий:

	| xc − xd |
tc−d =				ncnd (nc + nd − 2)				.	(2.10)
	~2	~2		n	c	+ n	d
	(nc −1)σc	+ (nd −1)σd

Можно показать, что если результаты измерений распределены нормально,

то tc-d имеет распределение Стьюдента с nc + nd–2 степенями свободы. Задаваясь определенной доверительной вероятностью Р, по таблице Ж.1 ме-

тодического пособия [2] можно найти соответствующее значение tр, и если tc−d < tp , то гипотеза о равенстве математических ожиданий принимается.

Распределением Стьюдента пользуются и в том случае, когда проверка равенства дисперсий в группах дала отрицательные результаты.

Если проведенные вычисления показали, что оценки дисперсий ~2 и сред-

σj

них x j групп наблюдений незначимо отличаются друг от друга, то группы на-

блюдений считаются равнорассеянными. Их можно объединить в один ряд и обрабатывать по алгоритму для прямых равнорассеянных результатов наблюдений.

Значимое различие групповых средних говорит о том, что на формирование результатов измерений большое влияние оказывает какой-то определенный фактор или группа факторов и совместная обработка таких результатов невозможна.

В том случае, когда значимо различие дисперсий ~2 , а средние групп j σj x яв-

ляется оценками одного и того же истинного значения измеряемой величины, группы результатов называются неравнорассеянными (неравноточными). Они обрабатываются по специфическому алгоритму, который приведен в [2, 3].

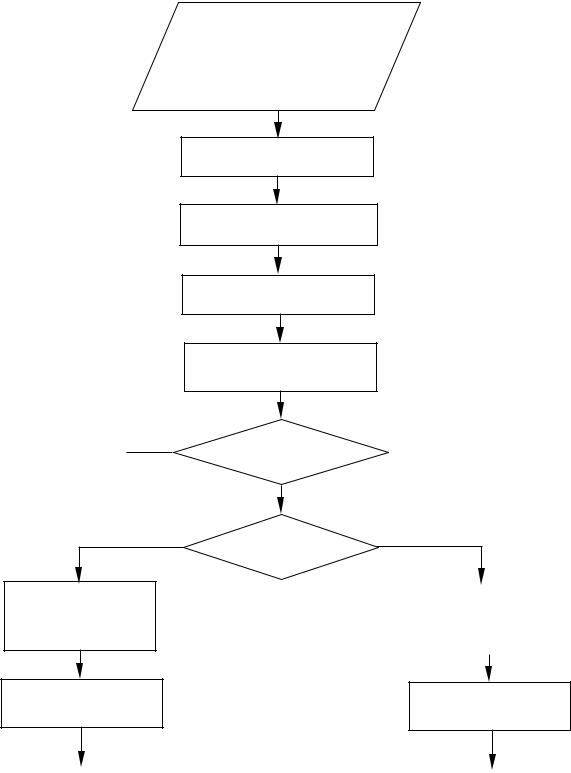
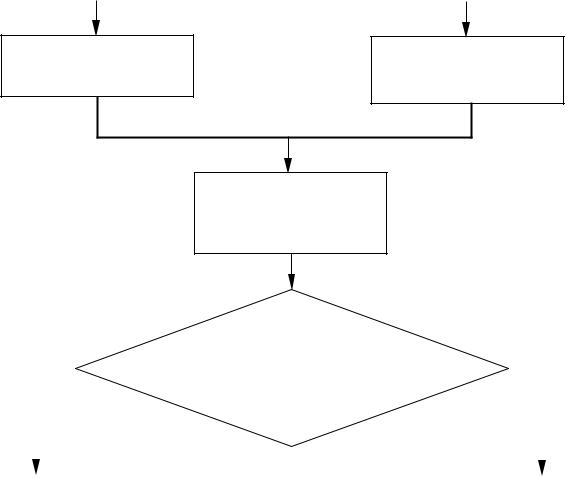
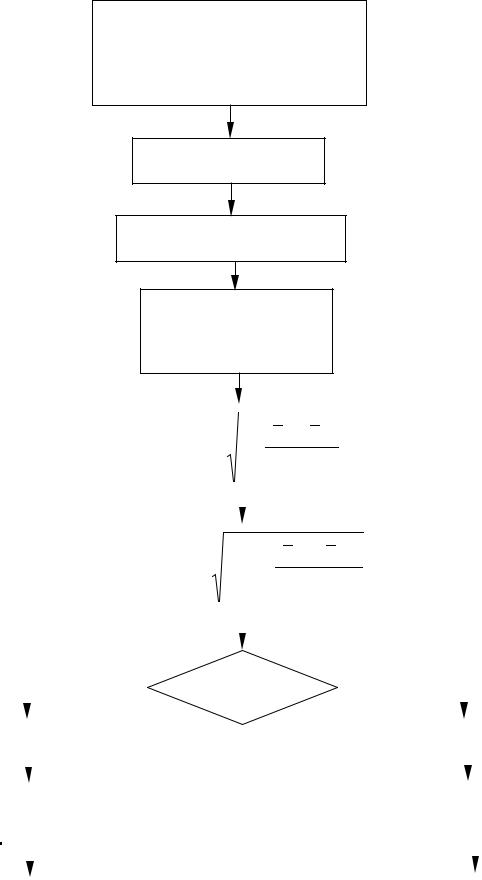
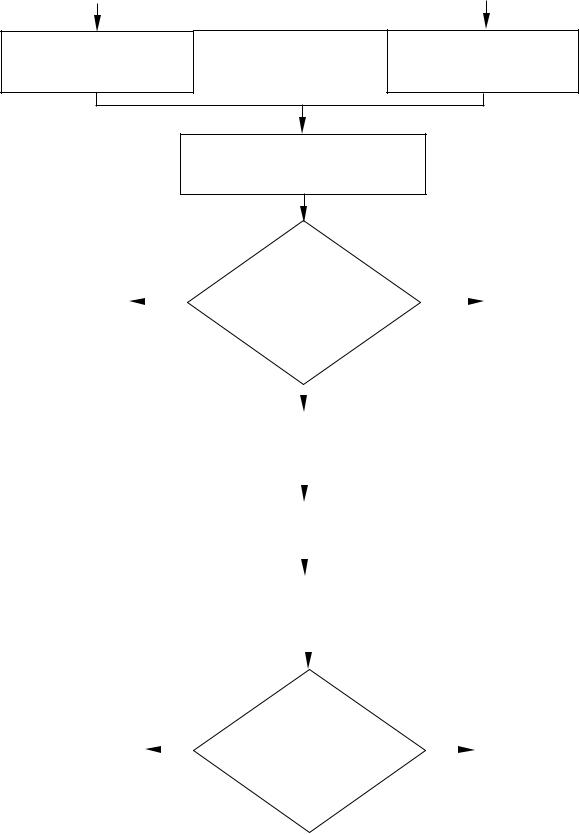
Алгоритмы предварительной совместной обработки двух и трех рядов наблюдений приведены на рисунках 2.1 и 2.2.

16

Значимы различия

математических ожиданий, нет

совместная обработка рядов наблюдений

невозможна

нет

σ~ хδ = σ~ х1

~ ~

σхм = σх2

Расчет ~2 2

σδ / σм

Исходные данные:

х11 , …, хn11;

х21 , …, хn22; q; Р

Расчет x1, x2

Расчет ~ х ~ х

σ 1 , σ 2

Расчет t x1−x2

Определение tP из P и n1+ n2 −2

t х1 −х2 ≤ t p

σ~ х1 < σ~ х2

Нет значимости да математическихразличий

ожиданий, совместная обработка рядов наблюдений

да возможна

~	~
σхδ	= σх2
~	~
σ х м	= σ х1

Расчет ~2 2

σδ / σм

А

Б

17

А

Кδ = nб – 1 = n1 - 1 Км = nм – 1 = n2 - 1

Б

Кδ = nδ – 1 = n2 - 1 Км = nм – 1 = n1 - 1

Определение

(Fnδ-1, nм-1) q из q, nδ-1, nм-1

Нет				Да
~2			2
		σδ	/ σм≤( Fnδ-1, nм-1) q

Группы результатов	Группы результатов
наблюдений	наблюдений
неравнорассеянных,	равнорассеянных,
дальнейшая обработка	дальнейшая обработка
неравнорассеянных	равнорассеянных
результатов	результатов
наблюдений	наблюдений

Рисунок 2.1 - Алгоритм предварительной совместной обработки двух рядов наблюдений

18

Исходные данные:

х11 , …, хn11; х12 , …, хn22;

х13 , …, хn33; q; m=3

Расчет x1, x2 , x3

Расчет σ~х1 , σ~х2 , σ~х3

m

Расчет х = ∑x j / m j=1

~

=

m (x j − x)2

Расчет σII

∑

m −1

j=1

~

nj m

(x ji − x j)2

Расчет σIII =

∑∑

N − m

i=1 j=1

Нет

Да

~

~

σII < σIII

N = n1 + n2 + n3

N = n1 + n2 + n3

~

~

~

~

σδ = σII

σδ = σIII

~

~

~

~

σм = σШ

σм = σII

Б

А

19

А

Б

Кδ = nδ – 1 = m - 1 Км = nм – 1 = N - m

Кδ = nб – 1 = N - m Км = nм – 1 = m - 1

Определение

(Fnδ-1, nм-1) q из q, nδ-1, nм-1

Значимость

Нет значимости

различия

различия

математических

Нет

~

2

~ 2

Да

математических

ожиданий,

совместная

σδ /

σм≤

ожиданий,

совместная

обработка рядов

≤ (Fnδ-1, nм-1) q

обработка рядов

наблюдений

наблюдений

невозможна

возможна

~

Нахождение

~

~

~

~

σmax и

σmin

из σx ,

σx

2

, σx

3

1

Расчет

~2

~

2

σmax / σmin

Кδ = nδ – 1 = nmax −1

Км = nм – 1 = N−1

Группы

Группы

результатов

Да

результатов

наблюдений

Нет

~2

~2

наблюдений

неравнорассеянны,

≤

равнорассеянны,

дальнейшая

σmax / σmin

дальнейшая

обработка

≤ (Fnδ-1, nм-1) q

обработка

неравнорассеян-

равнорассеянных

ных результатов

результатов

наблюдений

наблюдений

Рисунок 2.2 - Алгоритм предварительной совместной обработки трех рядов наблюдений

20