lektsii_ORE_2015

по оси х принимать значения, лежащие в пределах от -A до +A, причем координата этой проекции будет меняться со временем по закону:

.

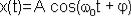Сумма двух гармонических колебаний одной частоты

	, , также будет гармоническим колебанием той
же	круговой	частоты:	=				.
		Значения	амплитуды			А	и
		начальной		фазы	φ	этого
		гармонического колебания				будет
		зависеть от		амплитуд	исходных
		колебаний	и	их начальных			фаз
		(Рис. 1.2). На рисунке 1.2.
		приведено два примера А и В
		сложения		гармонических
		колебаний	с	использованием
		метода векторных диаграмм. Из

векторных диаграмм видно, что направление (начальная фаза φ) и длина А вектора амплитуды суммарного гармонического колебания зависит, как от направления (от начальных фаз), так и от длины векторов амплитуд исходных гармонических колебаний.

Если угол (разность фаз: 1 2 ) между векторами А1 и А2 равен 0, то исходные колебания находятся в фазе и суммарная амплитуда (А =А1 +А2) будет максимальна.

Если угол (разность фаз: 1 2 ) между векторами А1 и А2 равен - π или π, то исходные колебания находятся в противофазе и

суммарная амплитуда (А = А1 -А2) будет минимальна

Если частоты колебани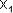й и 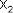, неодинаковы, векторы А1 и А2

будут вращаться с различной скоростью. В этом случае результирующий вектор А пульсирует по величине и вращается с не постоянной скоростью. Результирующим сигналом уже будет не гармоническое колебание, а сложный колебательный процесс.

Биения возникают при сложении колебаний, отличающихся по частоте на небольшую величину, и проявляются в появлении более низкочастотных изменений амплитуды суммарного сигнала, по сравнению с исходными частотами. Амплитуда колебаний при этом меняется от минимального значения равного разности исходных амплитуд до максимального значения, равного сумме амплитуд исходных колебаний, и вновь до минимального значения. Периодом биений является время повторения этого процесса (Рис

1.3.).

ЛЕКЦИЯ №3

2.3. Спектральный анализ сложного сигнала. Представление сигналов рядами Фурье

Представим сигнал в виде совокупности элементарных гармонических сигналов. Гармоническим называют сигнал, описываемый синусоидальной

функцией: S(t) = Amsin(wt +φ),
где Am амплитудное значение сигнала,	2 F -	круговая частота,
выражаемая в радианах, F = 1/T - частота сигнала, Т - период следования, φ -
начальная фаза сигнала.
Гармонический сигнал характерен	тем, что	он длится на

неограниченном интервале времени и не может быть разложен на элементарные составляющие.

Известно, что любой сложный периодический сигнал может быть представлен в виде суммы элементарных гармонических сигналов с помощью рядов Фурье. Это возможно, если функция, описывающая сигнал, отвечает условиям Дирихле:

1.Функция непрерывна на отрезке разложения;

2.В пределах периода T функция имеет конечное число максимумов и минимумов.

Пусть сигнал описывается функцией S(t), которая имеет частоту w = 2πF. Применяя разложение в ряд Фурье, получим:

,

(2)

где k = 1,2.3,... и т.д. - номера гармоник, а амплитуды разложения: ао, аки bк определяются из выражений:

,,

.

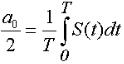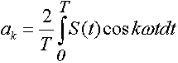Помимо формы (2) функцию S(t) можно представить в виде:

		a0
	S(t)		Ak cos(k t k )	(3)
	2		k 1

где: амплитуда A k и начальная фаза φk определяются из выражений:

							k arctg	bk
				(a2 b2 )		;
					k			ak

Любую периодическую функцию S(t) можно представить в виде

суммы слагаемых, каждое из которых является синусоидальным колебанием с амплитудой A k и начальной фазой φk.

Каждая составляющая сигнала с частотой kw называется гармоникой.

Колебание с частотой w называется первой гармоникой, с частотой 2w - второй гармоникой и т.п.

1.Совокупность амплитуд гармонических составляющих,

представленная как функция частоты называется амплитудным спектром сигнала (спектром амплитуд).

2. Совокупность значений φk гармоник сигнала, представленная на

интервале	0-360	град.,	называется	спектром	фаз.
Совокупность Ak		и φk полностью определяют частотный			спектр
сигнала.

Спектр амплитуд и спектр фаз для периодического сигнала

называют линейчатыми, так как они состоят из отдельных составляющих.

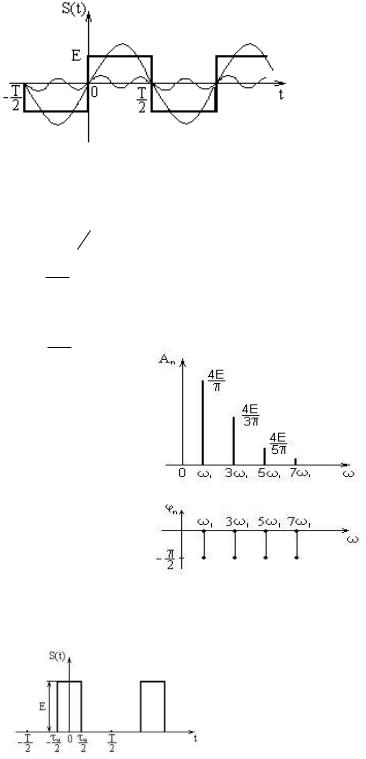
			Например,			для
		периодического				сигнала
		прямоугольной				формы,
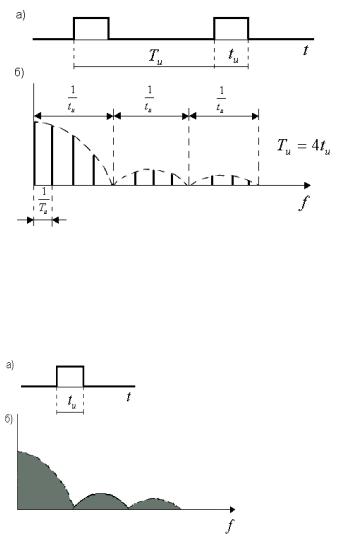
		показанного на рис.1,а спектр
		амплитуд имеет вид, показанный
		на рис.1,б.
		При	уменьшении			частоты
		периодического			сигнала число
		гармонических			составляющих в
		его
		спектре будет соответственно
		возрастать, стремясь в пределе
к бесконечности. Такой спектр
Рис.1	называется сплошным и получить его
	можно, используя не ряд, а интеграл Фурье. Для одиночного
прямоугольного импульса имеем спектр, показанный на рис. 2,б.
	В радиотехнике в качестве базисных
	функций	разложения		Фурье		используют
	преимущественно			тригонометрические
	функции. Это объясняется следующими
	причинами:
	а) функции cos wt, sin wt являются
	простыми, определены при всех значениях t,
	являются	ортогональными			и	составляют
	полный	набор	при кратном			уменьшении

периода; б) гармоническое колебание является единственной функцией времени,

сохраняющей свою форму при прохождении колебания через линейную систему с постоянными параметрами, может изменяться лишь амплитуда и фаза;

в) для гармонических функций и их комплексного анализа имеется мощный математический аппарат, найдены спектры множества форм сигналов;

г) гармоническое колебание легко осуществить на практике.

Кроме гармонического ряда Фурье применяются и другие типы разложения: по функциям Уолша, Бесселя, Хаара, полиномам Чебышева, Ляггера, Лежандра и др.

2.4.Спектры простейших периодических сигналов

а) Прямоугольное колебание (меандр) Для нечетной функции s(t)= -s(-t)

обращаются в ноль все коэффициенты an.

			T				T					T
			2 s(t)sin(n t)dt				2 sin(n t)dt
bn	2				4E					4E	( cos(n t))	2
	T			1	T				1	nT	1
		T		2		0				1		0

bn 2E (1 cos n ) n

bn = 0 для

bn 4E для n

четных	n	=	0,2,4...,
нечетных n = 1,3,5...

s(t)	4E	(sin t	1	sin 3 t	1	sin 5 t ... )
		1	3	1	5	1

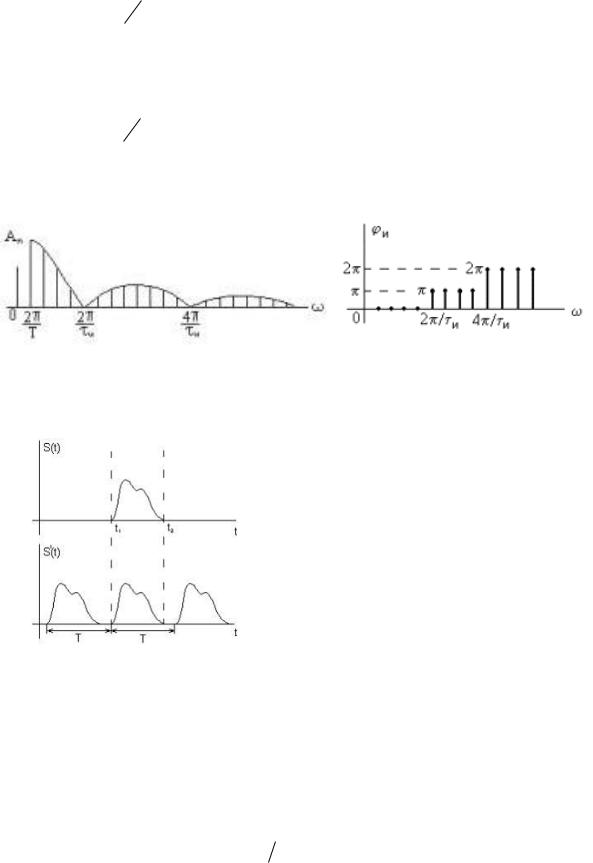
б) Последовательность униполярных прямоугольных импульсов

				и
а0		1		2		и E
				s(t)dt
2		T
			и
					2

bn = 0 - четная функция.

и

и

а

2

2

4E

2

2 n

2E

n

и

n

s(t) cos(n 1t)dt

cos(

t)dt

sin

2

T

T

n

T

и

0

2

;

E и

2E

1

n и

s(t)

sin

сos(n 1t)

T

n 1

n

Т

Чем меньше длительность импульса, тем шире спектр

2.5. Спектры непериодических сигналов

Пусть задан сигнал в виде ограниченной во времени функции s(t), отличной от нуля в промежутке t1t2. Выделим произвольный отрезок времени T, включающий промежуток t1t2, далее продолжим аналитически s(t) на всю бесконечную ось с периодом T. Тогда мы сможем разложить такую периодическую функцию s(t) в гармонический ряд Фурье. В комплексной форме будем иметь:

							T
		1	.		1	2
	s'(t)		Anei 1t			[ s'(t)e in 1t dt]ein 1t
		2 n		n 2 1				T
								2

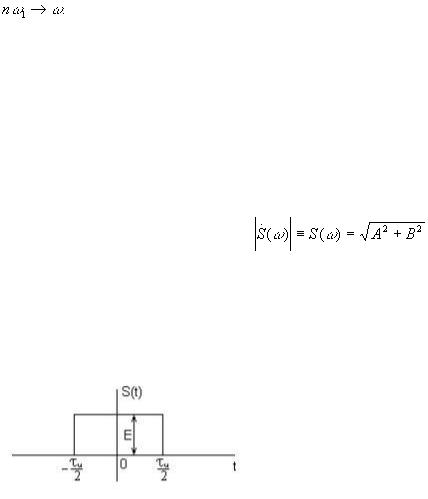
Полученный ряд на участке t1t2 будет точно соответствовать нашей функции s(t). Однако, в общем случае, чаще нас интересуют моменты времени за участком t1t2, и при этом необходимо увеличить период Т, т. е. отодвинуть повторные значения функции s(t). Производя замену переменных

и переходя от суммирования к интегрированию, получим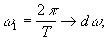

	2
s(t)	1					ei t			s(t)e i t dt d
	1				.					.
s(t)					S( )ei t d ;					S( )	s(t)e i t dt
		2

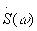- спектральная плотность сигнала s(t). Спектр непериодического сигнала

распространяется на отрицательные частоты.

где

сплошной (непрерывный) и

Если S( ) A( ) iB( ), то			- модуль спектральной
плотности – амплитудно-частотная характеристика.
( ) arctg	B( )	- фазово-частотная характеристика.
	A( )

Необходимое условие существования спектральной плотности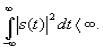

Пример. Спектр прямоугольного сигнала

и

E

.

2

S( )

i t

dt E e

i

dt

s(t)e

e

i

и

2

Согласно формуле Эйлера e i cos sin

i и		i и
2	е	2

,			и			sin			и
	2E							2
S( )		sin		E
			2		и			и

2

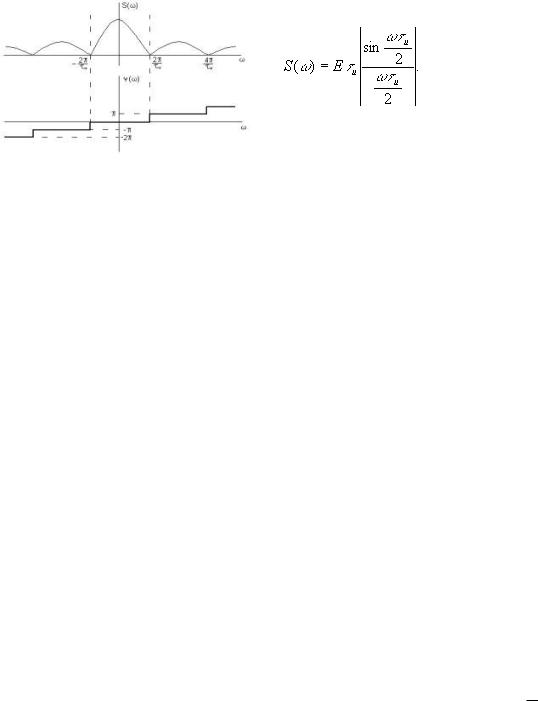
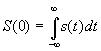- площадь под импульсом.

2.6. Свойства сигнала при применении преобразования Фурье

а) Сдвиг сигнала во времени s2(t)=s1(t-t0).

.			.
S 2 ( )	s2 (t)e i t dt	s1(t t0 )e i (t t0 )e i t0 d (t t0 ) e i t0 S1( )

Сдвиг во времени функции s(t) на ±t0 приводит к сдвигу фазы спектра на

±wt0.

б) Сжатие и расширение сигнала s2(t)=s1(nt).

,			i t	n		d (nt)		1 .
	s1	(nt)e									)
S2 ( )				n					S(
						n		n		n

При сжатии сигнала в n раз на временной оси во столько же раз расширяется его спектр на оси частот при уменьшении модуля в n раз.

Наоборот, при растяжении сигнала во времени имеет место сужение спектра и увеличение модуля спектральной плотности. Т. о. сжатие спектра импульса с целью повышения точности измерения частоты удлиняет время измерения.

Cжатие импульса по времени с целью, например, повышения точности измерения времени его появления заставляет расширять полосу пропускания измерительного устройства.

В теории преобразования Фурье доказывается, что и 12

Это соответствует принципу неопределенности: E t

в) Дифференцирование и интегрирование сигнала

при дифференц-и спектр умножается на iω,

											.
									2
		если			s (t)				1		S		( )ei t d
						1					1
	то	d		1				.						и	.	.
								S( )(i )e			i t				S2 ( )	i S1( )
		dt s1(t)		2								dt s2 (t);
	при интегрировании спектр делится на iω
	спектральная плотность интеграла s2 (t) s(t)dt равна															.	1	.
																S 2 ( )		S1( )
																	i

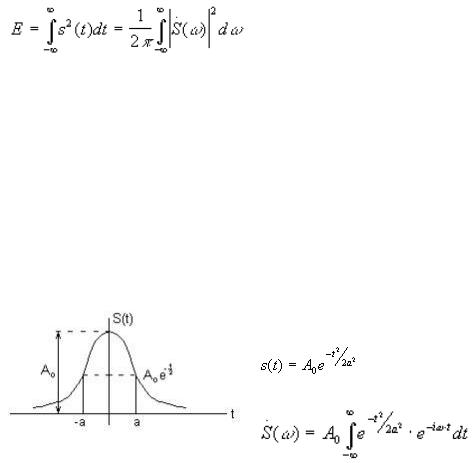
г) Сложение сигналов (линейность преобразования)

s(t) as1`(t) bs2 (t)

		.
		.	.
	S( )
		[as1 (t) bs2 (t)]e i t dt aS1 ( ) b S2 ( )

-из-за линейности операции интегрирования.

Вобщем случае спектральную функцию S(w), имеющую размерность [амплитуда/Гц], называют также плотностью амплитуд, спектральной плотностью, а иногда и просто спектром.

ЛЕКЦИЯ №4

2.7.Распределение энергии в спектре сигнала

В радиоэлектронике большое значение имеет Величина | S(w)| 2 , которая имеет физический смысл спектральной плотности энергии, т.е. энергии, приходящейся на полосу частот в 1 Гц, а полная энергия непериодического сигнала определяется через спектр квадрата функции s(t).

- равенство Парсеваля.

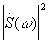- спектральная плотность энергии (энергия, приходящаяся на единицу полосы частот). Е - полная энергия сигнала.

Для энергии, приходящейся на конечную полосу частот (ω1-ω2), получим:

	1	2					1	2					1		2
		2						1							2
E 1 2				S( )		d				S( )		d					S( )		d
	2						2
		1						2							1
Распределение энергии непериодического сигнала ( импульса)
								Примеры. В радиоэлектронике наиболее
								часто используют импульс												со	Спектром
								Гауссова (колокольным спектром)
													,				-a < t < a,			а	- условная
								половина длительности на уровне 0,606.

.

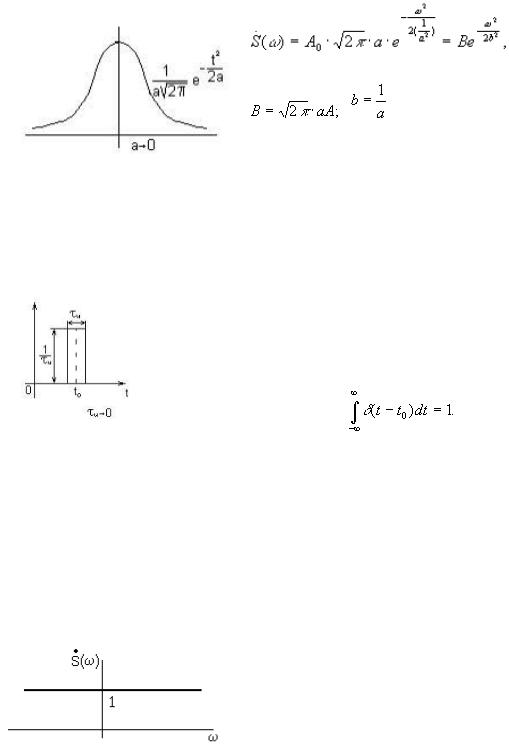
		т. е. спектр
Гауссова	импульса имеет	Гауссову форму:
	.
Можно показать, что такой		Гауссов импульс
обладает	наименьшим	произведением

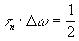при среднеквадратичном их определении., т.е наименьшую неопределенность и наименьшую ширину спектра , в которой сосредоточена вся энергия сигнала.

Спектр d-функции

В качестве d-функции может выступать сигнал любой формы с бесконечно малой длительностью и единичной площадью.

.

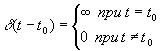Свойства d-функции

1) 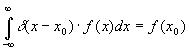- фильтрующее свойство., т.е s(t) x δ(t0) =s(t0)

2)Четность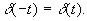

3)Нормировка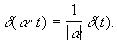

4)Спектральная плотность d-функции .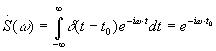

При t0 = 0, ,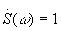

при t0 ¹= 0,( то есть во время действия импульса)

.

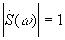Спектр выходного сигнала устройства является произведением спектра входного сигнала на комплексный коэффициент передачи устройства. Т.к. спектральная функция d - импульса равна 1, спектром импульсной переходной характеристики устройства является его комплексный коэффициент передачи.

2.8. Сигналы в канале радиосвязи

Классификация по виду передаваемых сообщений :

радиовещательные,

телевизионные,

телеграфные и т. д.

По полосе частот делятся на :

Узкополосные

широкополосные.

По выполняемым функциям сигналы в канале радиосвязи делятся на :

1)Управляющие сигналы (модулирующие),

Управляющие (модулирующие) сигналы – это сравнительно низкочастотные колебания, которые содержат полезную информацию, но непригодны для непосредственной передачи в эфир с помощью радиоволн.

это сигналы : звукового диапазона ( ТФ-300Гц -3400 Гц, Аудио -20 - 20000 Гц, Видеосигналы 50-6000 000 Гц), телеграфные сигналы (0-2400 Гц)

Первичные (Управляющие) сигналы сообщений имеют спектральный состав, расположенный в низкочастотной области в диапазоне от Ωmin до Ωmax. Отношение (Ωmax /Ωmin) всегда много больше 1. Поэтому такие сигналы являются широкополосными и не могут излучаться в пространство даже при значительной мощности, так как для эффективного излучения геометрические размеры антенны должны быть сравнимы с длиной волны излучаемого колебания.

Модуляция позволяет получить узкополосный сигнал, для спектра которого выполняется условие (ωmax /ωmin) ≈ 1

Модулирующие низкочастотные сигналы подразделяются на аналоговые, дискретные и цифровые.

2) Радиосигналы (модулированные) колебания.; Радиосигналы - высокочастотные почти гармонические

(квазигармонические) колебания, в которых амплитуда или мгновенная частота или фаза медленно меняются по некоторому закону.

Немодулированные ВЧ-колебания способны распространяться на большие расстояния, но не несут полезной информации.

В системе радиосвязи закон модуляции должен соответствовать закону изменения передаваемого управляющего низкочастотного сообщения

2.9. Модуляция сигналов Модуляция - процесс изменения одного или нескольких параметров

высокочастотного гармонического колебания. Модулированные колебания используются для передачи сообщений на расстояние .

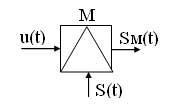
Модуляция осуществляется в устройствах модуляторах. Условное графическое обозначение модулятора имеет вид:

Несущая частота S(t) модулированного колебания - частота исходного высокочастотного гармонического колебания

К генератору несущей частоты предъявляются высокие требования к стабильности амплитуды и частоты.

Несущее колебание имеет вид S(t) =