4.Какие действия с целевой функцией не влияют на результат решения задачи линейного программирования?

Оптимальное решение задачи линейного программирования не изменится, если целевую функцию помножить на любое положительное число, либо прибавить к целевой функции любое число.

Доказательство этого утверждения можно провести самостоятельно, используя графический метод решения задачи линейного программирования.

Рассмотрим общую задачу линейного программирования:

Вектор α⁰ является оптимальным решением задачи (1) – (4) на максимум тогда и только тогда, когда α⁰ является оптимальным решением задачи (1^’)–(4^’) на минимум.

▲ Необходимость. Пусть W есть множество допустимых решений задачи (1)–(4) и задачи (1^’)–(4^’), а вектор α⁰ является оптимальным решением задачи (1)–(4) на максимум. Тогда, по определению глобального максимума, выполняется неравенство f(α⁰) ≥ f(α) для любого вектора α W. Умножив последнее неравенство на минус единицу, получим новое неравенство –f(α⁰) ≤ –f(α) и с учетом обозначения целевой функции задачи (1^’)–(4^’) имеем f₁(α⁰) ≤ f₁(α) для любого вектора α W. Откуда, по определению глобального минимума функции f₁(X), вектор α⁰ является оптимальным решением задачи (1^’)–(4^’) на минимум. Таким образом, необходимость доказана. Для доказательства достаточности следует провести рассуждения в обратной последовательности.■

Замечание. В дальнейшем будем рассматривать решение задач линейного программирования только на минимум, так как задача на максимум может быть сведена к соответствующей задаче на минимум.

13.Опишите последовательность решения канонической задачи линейного программирования с n переменными m линейных уравнений, если 1 n – m 2.

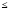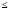Графическим методом можно решать задачу линейного программирования, если число переменных – n и число уравнений – m в системе ограничений этой задачи удовлетворяют соотношению 1 n – m 2.

Для этого необходимо:

• найти методом Гаусса общее решение системы линейных уравнений, которая является системой ограничений исходной задачи линейного программирования;

• исключив разрешенные переменные из полученного общего решения, получить систему из m неравенств с (n–m) переменными;

• из полученного общего решения выразить разрешенные переменные через свободные переменные и подставить их в целевую функцию, которая станет функцией (n–m) свободных переменных;

• решить графическим методом полученную задачу линейного программирования с (n–m) свободными переменными, с ограничениями в виде m неравенствами, а также с ограничениями на знак переменных;

• найденные свободные переменные подставить в общее решение, вычислить значения разрешенных переменных и записать оптимальное решение исходной задачи.

16.Сформулируйте теорему о существовании опорного решения.

Теорема (о существовании опорного решения). Если каноническая задача линейного программирования имеет хотя бы одно допустимое решение, то эта задача имеет и опорное решение.

Доказательство

Рассмотрим КЗЛП

(1)f(X) = 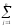γ_j x_j + γ₀,

(2)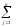А_j x_j =B,

(3)x_j ≥ 0, j = 1,2,…,n,

которая имеет хотя бы одно допустимое решение. Из всех допустимых решений данной задачи выберем допустимое решение с наименьшим числом ненулевых координат. Пусть таким решением будет вектор α = ( α₁, …, α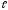, 0, …, 0), где координаты α₁> 0, …, α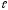> 0 (координаты всегда можно перенумеровать так, что первыми из них станут ненулевые) и докажем, что выбранный вектор является опорным решением задачи (1) – (3).

Предположим противное, а именно, что вектор α не является опорным решением. Тогда по определению опорного решения, векторы A₁, A₂, … A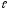, соответствующие ненулевым координатам выбранного вектора α, образуют линейно зависимую систему. Из определения линейно зависимой системы векторов следует, что найдется ненулевой набор чисел k₁, k₂, …k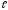 такой, что будет выполняться соотношение

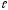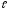(1)A₁ k₁ + A₂ k₂ + … + A k = Ө.

Так как вектор α является допустимым решением рассматриваемой задачи, то по определению, этот вектор является решением системы линейных уравнений (2). Тогда по определению решения системы уравнений должно выполняться соотношение

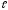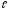(2)A₁ α ₁ + A₂ α ₂ + … + A α = В.

Прибавив к соотношению (5) соотношение (4), умноженное на 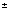δ, получим

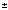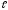
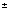А₁( α₁ δ k₁) + А₂ ( α₂ δ k₂ ) + … + А(α δ k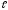 ) = B.

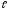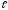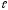Из последнего соотношения по определению решения системы уравнений следует, что векторы α^’ = ( α₁ + δ k₁, α₂ + δ k₂, … α + δ k, 0, …, 0) и α^” = (α₁ – δ k₁, α₂ – δ k₂, … α – δ k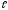, 0. …. 0 ) являются решениями системы линейных уравнений (2). Если же число δ выбрать так, что оно удовлетворяет арифметической лемме, то координаты векторов α^’ и α^” будут удовлетворять условию (3), а сами векторы будут являться допустимыми решениями задачи (1)–(3) и при этом, хотя бы у одного из этих векторов число ненулевых координат будет меньше, чем . 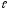Это противоречит выбору допустимого вектора α. Следовательно, вектор α является опорным решением задачи (1)–(3).