29.Каков критерий выбора разрешающего элемента для перехода к новому опорному решению?

Рассмотрим каноническую задачу линейного программирования

1. f(X) = γ_j x_j + γ₀,

2. А_j x_j =B,

3. x_j ≥ 0, j=1,2,…,n.

Пусть вектор α опорное решение данной задачи. Выберем некоторый базис этого опорного решения, например,

В₁ , …, В_l , …, В_k , …, В_r, т.е., опорное решение имеет вид

α = ( 0, …, 0, α₁, 0, …,, 0, α_l, 0, …, 0, α_k, 0,…, 0, α_r, 0, 0, .., 0).

Приведя систему векторов условий к базису выбранного опорного решения, получим симплекс таблицу

…

B1^’

…

Bl^’

…

Bk^’

…

Br^’

…

As^’

…

B^’

…

1

…

0

…

0

…

0

…

a’1s

…

α1

…

…

…

…

…

…

…

…

…

…

…

…

(4)

…

0

…

1

…

0

…

0

…

a’ls

…

αl

…

…

…

…

…

…

…

…

…

…

…

…

…

0

…

0

…

1

…

0

…

a’ks

…

αk

…

…

…

…

…

…

…

…

…

…

…

…

…

0

…

0

…

0

…

1

…

a’rs

…

αr

…

0

…

0

…

0

…

0

…

δs

…

δ0

. Если оценка s-го столбца положительная, т.е. δ_s > 0, где s=1, 2, …, n, но при этом среди элементов этого столбца найдется положительный, т.е, α’_is >0, i=1, 2, …, r , то рассматриваются отношения вида для всехa’_is > 0 , среди которых выбирается наименьшее. Пусть это будет отношение

= {}.

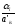Затем проводится преобразование Жордана симплекс таблицы (4) с разрешающим элементом α’_ks. При этом k-ю строку помножаем на 1 / α’_ks , далее эту же строку поочередно прибавляем к строке i, где i = 1, 2, …, r, и к строке оценок, предварительно помножив соответственно на величину (–α’_is) и на (–δ_s) .После такого преобразования будет получена симплекс таблица (5), приведенная к базису, отличному от предыдущего, так как вектор В_k уступил место вектору А_s.

…	B1’^’	…	Bl^’’	…	Bk^’’	…	Br^’’	…	As^’’	…	B^’’
…	1	…	0	…	–a’1s / a’ks	…	0	…	0	…	α1–a’1s αk / a’ks
…	…	…	…	…	…	…	…	…	…	…	…
…	0	…	1	…	–a’ls / a’ks	…	0	…	0	…	αl–a’1s αk / a’ks
…	…	…	…	…	…	…	…	…	…	…	…
…	0	…	0	…	1 / a’ks	…	0	…	1	…	αk / a’ks
…	…	…	…	…	…	…	…	…	…	…	…
…	0	…	0	…	–a’rs / a’ks	…	1	…	0	…	αr–a’rs αk / a’ks
…	0	…	0	…	–δs / a’ks	…	0	…	0	…	δ0–δs αk / a’ks

Симплекс таблица (5) обладает следующими свойствами:

1⁰. Она приведена к базису В₁, …, B_l, …, B_k–1, B_k+1, …, B_r, …, A_s.

2⁰_. Все элементы столбца ограничений неотрицательные.

33.Записать искусственную задачу для данной канонической задачи линейного программирования и теорему о существовании опорного решения кзлп.

Решение канонической задачи линейного программирования симплекс методом всегда начинается с некоторого начального опорного решения. До сих пор начальное опорное решение задавали, либо для его нахождения выбирался такой базис системы векторов условий, чтобы вектор ограничений линейно раскладывался с неотрицательными коэффициентами. Такой способ нахождения начального опорного решения может потребовать перебора большого числа различных базисов. Этого можно избежать, если для нахождения начального опорного решения использовать более эффективный метод – метод искусственного базиса.

Рассмотрим каноническую задачу линейного программирования

1. f(X) = γ_j x_j + γ₀ (min),

2. А_j x_j =B,

3. x_j ≥ 0, j = 1, 2, …, n.

Построим для задачи (1) – (3) искусственную каноническую задачу линейного программирования вида:

4. φ(X) = x_n+1 + x_n+2 + … +x_n+m (min),

5. А_j x_j +E₁ x_n+1 + E₂ x_n+2 + … + E_m x_n+m =B,

6. x_j ≥ 0, j=1,2,…,n, n+1, n+2, … , n+m,

где E_j – единичный вектор (j = 1, 2, …, m) , а x_n+1 , x_n+2 , … , x_n+m – искусственные переменные.

Теорема (о существовании опорного решения). Если каноническая задача линейного программирования имеет хотя бы одно допустимое решение, то эта задача имеет и опорное решение.

▲ Рассмотрим КЗЛП

1. f(X) = γ_j x_j + γ₀,

2. А_j x_j =B,

3. x_j ≥ 0, j = 1,2,…,n,

которая имеет хотя бы одно допустимое решение. Из всех допустимых решений данной задачи выберем допустимое решение с наименьшим числом ненулевых координат. Пусть таким решением будет вектор α = ( α₁, …, α, 0, …, 0), где координаты α₁> 0, …, α> 0 (координаты всегда можно перенумеровать так, что первыми из них станут ненулевые) и докажем, что выбранный вектор является опорным решением задачи (1) – (3).

Предположим противное, а именно, что вектор α не является опорным решением. Тогда по определению опорного решения, векторы A₁, A₂, … A, соответствующие ненулевым координатам выбранного вектора α, образуют линейно зависимую систему. Из определения линейно зависимой системы векторов следует, что найдется ненулевой набор чисел k₁, k₂, …k такой, что будет выполняться соотношение

4. A₁ k₁ + A₂ k₂ + … + Ak= Ө.

Так как вектор α является допустимым решением рассматриваемой задачи, то по определению, этот вектор является решением системы линейных уравнений (2). Тогда по определению решения системы уравнений должно выполняться соотношение

5. A₁ α ₁ + A₂ α ₂ + … + A α = В.

Прибавив к соотношению (5) соотношение (4), умноженное на δ, получим

А₁( α₁ δ k₁) + А₂ ( α₂ δ k₂ ) + … + А(α δ k ) = B.

Из последнего соотношения по определению решения системы уравнений следует, что векторы α^’ = ( α₁ + δ k₁, α₂ + δ k₂, … α + δ k, 0, …, 0) и α^” = (α₁ – δ k₁, α₂ – δ k₂, … α – δ k, 0. …. 0 ) являются решениями системы линейных уравнений (2). Если же число δ выбрать так, что оно удовлетворяет арифметической лемме, то координаты векторов α^’ и α^” будут удовлетворять условию (3), а сами векторы будут являться допустимыми решениями задачи (1)–(3) и при этом, хотя бы у одного из этих векторов число ненулевых координат будет меньше, чем . Это противоречит выбору допустимого вектора α. Следовательно, вектор α является опорным решением задачи (1)–(3).