лекции 8-14 / LEC_14a

14. Планарный диэлектрический волновод

Найдем моды планарного волновода – слоя среды с показателем

преломления	ε1	в области	−l < z < l , окруженного средой с	показателем
преломления	ε2 .	Среды считаем прозрачными, Im ε1,2 = 0 . Без		ограничения
общности можно		считать	ε2 =1 (модовая структура зависит	только от

соотношения показателей преломления ε1 и ε2 ).

Начнем рассмотрение с излучения, обладающего s-поляризацией.

Уравнение (13.3) принимает вид
d 2 E	+α2 E = 0,	α2	=	ω2	ε1 −κ2		(| z |< l),
dz2				c2			(14.1)
d 2 E						ω2
	− p2 E = 0,	p2	=	κ2 −			(| z |> l).
dz2						c2

Из требования конечности поля при | z |→ ∞ следует p2 > 0 . Заметим также, что

p2 +	α2 =	ω2	(ε1 −1).		(14.2)
		c2
В силу с имметрии задачи по отношению к замене z → −z , если задача
имеет решение E1			= E(z) , то	решением будет и	E2 = E(−z) . Тогда	из-за
линейности	рассматриваемой			задачи решениями	будут служить	также
E(+) = E(z) + E(−z)			(четная функция z) и E(−) = E(z) − E(−z) (нечетная функция

z). Поэтому достаточно рассматривать поотдельности распределения с четными и нечетными по z зависимостями, то есть четные и нечетные моды.

Для четных мод

Acosαz	| z |< l,
E =	| z |> l.
B exp(−p | z |)

Сшивание решений при | z |= l заключается в приравнивании этом значении z, что приводит к условиям

(14.3)

E и dE / dz при

Acosαl = B exp(−pl), αAsinαl = pB exp(−pl).

Отсюда

αl tg(αl) = pl .

(14.4)

Соотношение (4) вместе с (2), представленном в виде

	( pl)2 +(αl)2 =	ω2	l 2	(ε1 −1),	(14.5)
		c2

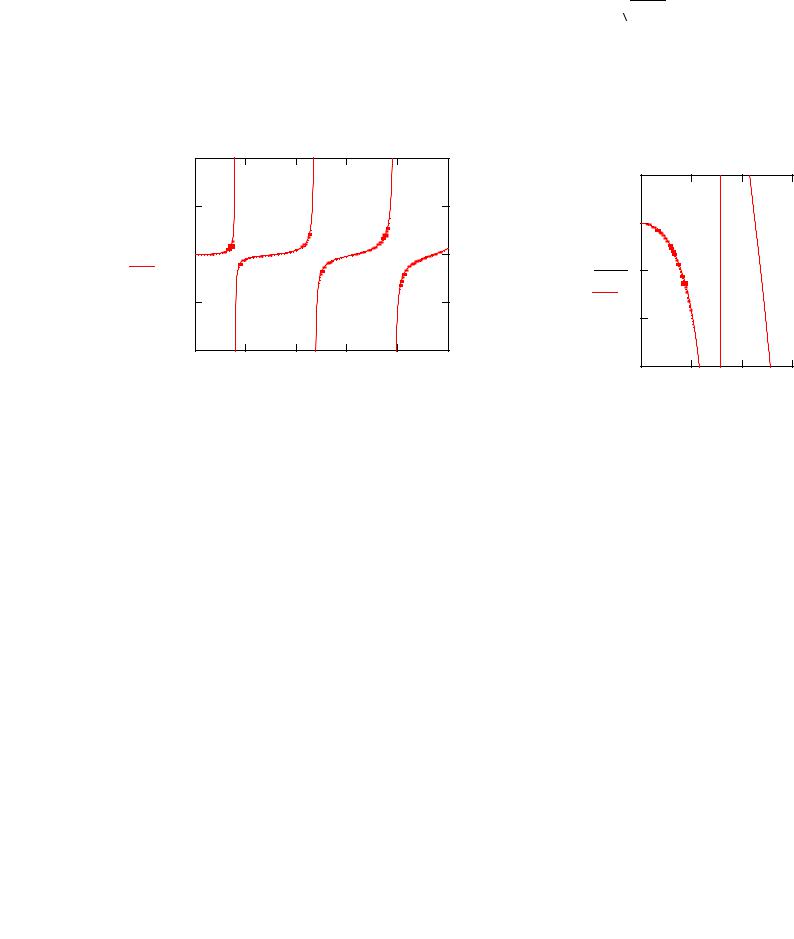
служит дисперсионным уравнением, задающим связь между частотой излучения ω и постоянной распространения κ . При фиксированной частоте отсюда определяется постоянная распространения. Решение удобно найти графически как точки пересечения в квадранте плоскости {αl > 0, pl > 0} линий

(4) и окружностей (5) (см. рис.). Если радиус окружности (равный ωc lε1 −1 )

меньше π , точка пересечения единственная, так что существует только одна четная мода с s-поляризацией. Такая мода имеется и для произвольно малых толщин волновода или частот; в этом случае говорят, что частота отсечки этой моды равна нулю. При больших радиусах число мод увеличивается, так что волновод с достаточно большой шириной будет многомодовым.

	100
								2
	50
								1
x tan(x)	0						x
								0
							tan(x)
	− 50
							− 1
− 100		2	4	6	8	10
							− 2
				x					2	4
Аналогично для нечетных мод решение имеет вид										x

Asinαz	| z |< l,
E =	| z |> l.
B exp(−p | z |)

Дисперсионное уравнение вместо (4) принимает форму

αl ctg(αl) = −pl ,

(14.6)

тогда как вид соотношения (5) сохраняется. Графический анализ (5) и (6) показывает, что все нечетные моды обладают ненулевой частотой отсечки.

Для излучения с p-поляризацией исходным служит уравнение (13.6) для напряженности магнитного поля H. Вместо уравнений (1) теперь имеем

d 2 H	+α2 H = 0	(| z |< l),
dz2		(14.7)
d 2 H
	− p2 H = 0	(| z |> l).
dz2

На границах слоя непрерывными должны быть величины H и	1 dH .
	ε dz

Аналогично предыдущему, легко получить дисперсионные уравнения для четных мод (ненулевая частота отсечки у единственной моды)

1

ε1 αl tg(αl) = pl (14.8)

инечетных мод (все такие моды обладают ненулевой частотой отсечки)

1	αl ctg(αl) = −pl.	(14.9)
ε1

Таким же образом можно найти модовую структуру многослойных планарных волноводов. При этом в несимметричных структурах уже нарушается разделение мод на четные и нечетные.

Волны в периодических структурах

Рассмотрим распространение излучения в структуре с периодическим изменением диэлектрической проницаемости, когда уравнение (13.3) принимает вид

d 2 E	+k 2 (z)E = 0,	(14.10)
dz2

где k 2 (z) - периодическая функция, например:

	k 2 (z) = k 2 [1+ µcos(2Kz)], k 2 =	ω2	ε0 = const.	(14.11)
		c2

Уравнение (10) с периодической функцией k 2 (z) называется уравнением

Хилла, а его частный случай с соотношением (11) – уравнением Матье. Теория таких уравнений хорошо разработана, но решения как правило выражаются через специальные функции. Поэтому здесь приведем только приближенные решения для случая малой глубины модуляции показателя преломления µ <<1.

Ищем решение в виде суперпозиции двух квазиплоских волн, распространяющихся во встречных направлениях

E = Aexp(ikz) + B exp(−ikz).

(14.12)

Амплитуды A и B предполагаются медленно изменяющимися на масштабе 1/k. Поэтому

d 2 E	≈ −k	2	dA	exp(ikz) −	dB		(14.13)
dz2			E +2ik		dz	exp(−ikz) .
			dz

В зависимости от соотношения между k и K имеет место ряд острых резонансов. При малых глубинах модуляции основной резонанс наблюдается при малых расстройках ∆ = k − K . В этом случае, сохраняя после подстановки (12) и (13) в (10) только резонансные члены (типа плоских волн с близким к k волновым числом), получим уравнения

	dA	= i	µk B exp(−2i∆z),
	dz		4	(14.14)
	dB	= −i µk
				Aexp(2i∆z).
	dz		4

Исключим из системы (14) B:

d 2 A	+2i∆	dA		µk		2	(14.15)
dz2		dz	−	4		A = 0.

Общее решение (15) имеет вид

A =[C exp(	(kµ / 4)2 −∆2 z) +C		2	exp(− (kµ / 4)2		−∆2 z)].		(14.16)
1

Рассмотрим случай полуограниченной среды с периодическим изменением показателя преломления (0 < z < +∞). Если подкоренное выражение в (16) положительно, то, так как в прозрачной среде невозможно неограниченное возрастание интенсивности, следует положить C1 = 0. Тогда поле при больших z будет экспоненциально убывать. Это означает, что при таких условиях (область непрозрачности) рассматриваемая среда полностью отражает падающее на нее излучение. При отрицательном знаке подкоренного выражения волна распространяется в среде, но с измененным соотношением между частотой и эффективным волновым числом k (см. рис.).

Градиентный волновод (квадратичная неоднородность)

В квазиоптическом приближении

2ik	∂E	+∆ E +k2 δε E = 0 .		(14.17)
	∂z		ε0
Для щелевых пучков
2ik	∂E	+ ∂2 E	+k2 δε E = 0 .	(14.18)
	∂z	∂x2	ε0

Среда с квадратичным поперечным профилем диэлектрической проницаемости

	δε	= −δε	0	x2	.	(14.19)
	ε0			h2

Тогда

2ik	∂E		∂2 E	2	x2	E = 0 .
	∂z	+	∂x2	−k δε0
					h2

Разделение переменных

E(x, z) = X (x)eiβz .

d	2				2
		X2	−	2kβ +k2δε0	x	X = 0.
					2
dx					h

Ищем решение в виде гауссова пучка

X = e−x2 /w2 .

После подстановки (23) в (22) получаем

(14.20)

(14.21)

(14.22)

(14.23)

	β = −	1	< 0,	1	=	k2δε0	(δε	0	> 0)	(14.24)
		kw2		w4		4h2

Это фундаментальная мода (гауссов пучок низшего порядка). Существуют и гауссовы пучки высших порядков, для которых вместо (23) Xn = Pn (x)e−x2 /w2 , где Pn (x) - полином степени n.

Задание: обобщить рассмотрение на случай поперечно двумерной квадратичной неоднородности.