Жидкость, подчиняющаяся закону теплопроводности Фурье.

Для широкого класса изотропных сред справедлив закон теплопроводности Фурье: количество тепла dq, прошедшее внутрь за время dt через площадку dS с нормалью n, пропор­ционально dS dt и производной от температуры по нормали:

dq = k dT dS dt.

dn

Для потока тепла t_n, введенного ранее, закон Фурье дает

(1.3.56)

При выводе уравнения энергии было показано, что t_n, —проек­ция на нормаль вектора потока тепла t, т. е. t_n=(t·n).

Производная . Таким образом (1.3.56) равносильно соотношение

(1.3.57)

Равенства (1.3.56) и (1.3.57) – запись закона теплопроводности Фурье.

Коэффициент k — коэффициент теплопроводности. Величина k различна для разных жидкостей и зависит в основном от температуры. Обычно вводят число, называемое числом Прандтля и коэффициент теплопроводности k выражают через μ и Pr. В некоторых случаях число Pr оказывается постоянным.

Для многоатомных газов вычисление k связано со сложными расчетами и экспериментами. Для капельных жидкостей в узких интервалах температур пользуются линейной зависимостью

k = k₀+α(T-T₀).

В смесях газов там, где существенна диф­фузия, вектор потока тепла t начинает зависеть не только от гра­диента температуры, но и от градиента концентрации.

В неизотропных средах вместо скалярного коэффициента теплопроводности k приходится вводить тензор теплопровод­ности К.

Дифференциальная запись закона сохранения энергии

Используем формулу

для преобразования интеграла, связанного с вектором теплового потока

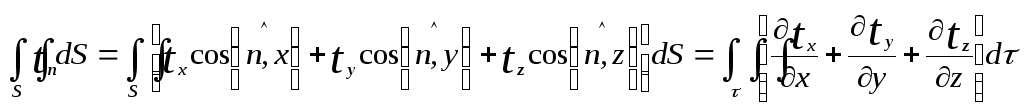(1.3.58)

Подставим (1.3.58) в выражение, представляющее закон сохранения энергии в интегральном виде

(1.3.59)

Равенство (1.3.59) справедливо для любого объема. Следовательно

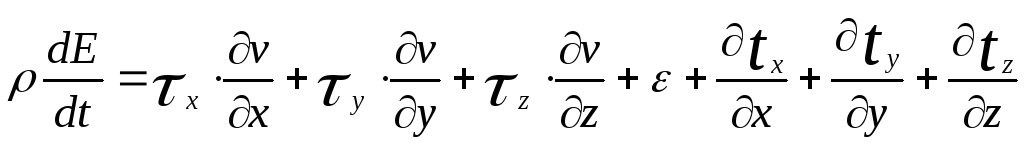(1.3.60)

Равенство (1.3.60) – запись закона сохранения энергии в дифференциальной форме.

3. УРАВНЕНИЯ РАВНОВЕСИЯ ЖИДКОСТИ И ГАЗА

1. Уравнения равновесия и условия их разрешимости.

Уравнения равновесия. Условия разрешимости системы уравнений равновесия. Условия на поверхности раздела двух жидкостей. Равновесие однородной несжимаемой жидкости.

Уравнения равновесия и условия их разрешимости

Рассмотрим покоящуюся жидкость. В этом случае в жидкости наблюдаются только нормальные напряжения, причем их величина не зависит от ориентировки площадки. В данном случае для задач о равновесии жидкости не существенно различие между идеальной и вязкой жидкостью. Предположим, что у жидкости нет внутреннего момента и что для нее справедлив закон теплопроводности Фурье.

Запишем систему уравнений гидромеханики в общем виде

(1.4.1)

(1.4.2)

(1.4.3)

(1.4.4)

Так как жидкость находится в равновесии, то это означает, что υ≡0 и

, а тогда для любой функции f:

Имея это в виду, обратимся к системе уравнений (1.4.1) – (1.4.4). Уравнение неразрывности (1.4.1) выполняется автоматически. Закон количества движение (1.4.2) в силу равенств τ_x = -ip, τ_y = -jp, τ_z = -kp запишется в виде

(1.4.5)

Уравнение энергии примет вид

(1.4.6)

Уравнения (1.4.4), (1.4.5), (1.4.6) образуют систему уравнений равновесия. Предполагая, что объемных источников тепла нет, т. е. ε=0, и учитывая закон Фурье t = k grad T, где k = k(p,T), получим систему уравнений равновесия в виде

(1.4.7)

(1.4.8)

(1.4.9)

В системе уравнений равновесия пять уравнений, а искомых функций три: ρ, p,T. Система переопределена. Это означает, что равновесие возможно не всегда. Получим условия разрешимости системы (1.4.7) – (1.4.9).

Выпишем уравнения (1.4.7) в проекциях:

(1.4.10)

Продифференцируем первое уравнение по y, второе по x и вычтем одно из другого. Получим

(1.4.11)

Аналогично получим еще два уравнения

(1.4.12)

(1.4.13)

Умножая (1.4.11) на F_z, (1.4.12) на F_x, (1.4.13) на F_y и складывая, получим

(1.4.14)

или в векторном виде F = rot F = 0.

Условие (1.4.14) необходимо для возможности равновесия. Это условие есть необходимое и достаточное условие для того, чтобы векторное поле F имело вид

F = B grad V, (1.4.15)

где B и V – некоторые функции координат.

Подставляя (1.4.15) в (1.4.7) получаем

(1.4.16)

(1.4.17)

Аналогично получим

,

Равенства (1.4.17) означают, что между p и V имеется функциональная зависимость

V = Q (p). (1.4.18)

Равенство (1.4.14) и эквивалентное ему равенство (1.4.15) дает общий вид сил, при которых возможно равновесие. При выполнении (1.4.14) силовые линии ортогональны к поверхностям V = const. Направление F параллельно grad V.

Условия на поверхности раздела двух жидкостей

Пусть имеются несжимаемые жидкости 1 и 2, разделенные поверхностью ∑, причем ρ¹ ≠ ρ². Равенство напряжений в точках поверхности раздела в случае равновесия дает условие

(1.4.19)

Для каждой из жидкостей справедливы уравнения равновесия

, ,;

(1.4.20)

, ,.

Умножим первое уравнение на dx, второе на dy, третье на dz и сложим полученные выражения.

(1.4.21)

Аналогично

(1.4.22)

Пусть dx, dy, dz – проекции dr – перемещения вдоль поверхности

раздела ∑.

Тогда в силу (1.4.19)

(1.4.23)

Вычитая (1.4.22) из (1.4.21) и учитывая (1.4.23), получаем

(1.4.24)

Так как ρ¹ ≠ ρ² по предположению, то из (1.4.24) следует, что вдоль поверхности раздела

или F·dr = 0 (1.4.25),

т.е. в каждой точке поверхности ее элемент ортогонален вектору силы F. Равенство (1.4.25) означает, что работа массовых сил при перемещении вдоль поверхности раздела равна нулю.

Если считать силы тяжести направленными вертикально, то поверхностями раздела будут горизонтальные плоскости. Если принять, что силы тяжести направлены к центру земли, то поверхностями будут сферы.

Равновесие однородной несжимаемой жидкости

Система уравнений равновесия содержит уравнения (1.4.7)— (1.4.9). Уравнение состояния (1.4.9) для однородной несжимаемой жидкости имеет вид . Учитывая это, можно урав­нение (1.4.7) записать в виде

(1.4.26)

т. е. равновесие несжимаемой жидкости возможно только в по­тенциальном силовом поле. Пусть

Тогда из (4.1) и (4.2) следует, что , т. е.

Постоянная интегрирования С находится из условия .Таким образом, давление найдено.

Если массовые силы — силы тяжести, то F_х = F_у = 0, F_z = = — g и потенциал V = gz.. Из формулы (1.4.26) в этом случае получаем гидростатический закон:

Для несжимаемой жидкости коэффициент теплопроводности за­висит от температуры или постоянен. Если k=k(T), то урав­нение (1.4.8) для температуры — нелинейное уравнение в частных производных второго порядка. В случае k=const уравнение (1.8) переходит в уравнение Лапласа

Функции, являющиеся решением уравнения Лапласа, называют­ся гармоническими. Следовательно, в рассматриваемом случае Т есть гармоническая функция.

Для решения уравнения Лапласа должны быть заданы гра­ничные условия. Чаще всего встречаются два типа граничных условий и соответственно формулируются две краевые задачи.

1. На поверхности S заданы значения температуры, т. е. — заданная функция точек поверхности (задача Дирихле).

2. На поверхности S задается значение нормальной производной (задача Неймана)

Это означает, что общее количество тепла, входящее и выходящее через поверхность S, равно нулю. При равновесии это условие выполнимо.

Если решать внешнюю задачу Неймана для безграничной области, то условие для потока тепла не ставится — тепло рас­сеивается.

Таким образом, в случае однородной несжимаемой жидкости задача об определении температуры решается независимо от задачи об определении давления.

2. Равновесие баротропной жидкости.

Понятие о баротропной и бароклинной жидкости. Равновесие баротропной жидкости. Частные случаи баротропных процессов: несжимаемая жидкость, изотермический процесс, адиабатический процесс.

Понятие о баротропной и бароклинной жидкости

Жидкость называется баротропной, если ее плотность есть функция только давления

Ρ = Ф(p). (1.4.27)

В противном случае жидкость называется бароклинной. Пред­положим, что жидкость баротропна, и выпишем уравнения рав­новесия, учитывая (1.4.26):

, ,. (1.4.28)

Введем в рассмотрение функцию

. (1.4.29)

Для P(p) справедливы равенства

, ,(1.4.30)

Система (1.4.27) с учетом (1.4.29) примет вид

, ,. (1.4.31)

Из (1.4.30) следует, что массовые силы F должны быть потенциальны, т.е. равновесие возможно, если поле массовых сил консервативно. Пусть

F = - grad V,

где V – потенциал массовых сил. Тогда из (1.4.30) следует

, ,,. (1.4.32)

Проинтегрируем (1.4.31) и получим

. (1.4.33)

Постоянная С находится из условия . Определивp и подставив его в (1.4.27), получим ρ. Давление и плотность постоянны на поверхностях V = const.

Если жидкость находится при постоянной температуре (изотермична) Т = Т₀, то уравнение равновесия для температуры удовлетворяется тождественно. А уравнение состояния принимает вид

,

т.е. плотность есть функция только давления – жидкость баротропна.

В случае адиабатического процесса (отсутствие притока тепла извне)

,

где k – показатель адиабаты, равный отношению теплоемкостей газа при постоянном давлении c_p и постоянном объеме c_v. Для воздуха k = 1,405. Значения величин p₀, ρ₀, Т₀ относятся к какой-нибудь характерной точке покоящегося газа.

Рассмотрим равновесие жидкости при отсутствии массовых сил,

т.е. F =0. В этом случае grad p = 0 и p = const. (см. Уравнения равновесии и условия их разрешимости (1.4.7)).

Примечание:

Как известно, между давлением р и плотностью ρ существует функ­циональная зависимость.

Жидкость, для которой ρ есть функция только р, обычно называют баротропной. При этом имеется в виду, что зависимость ρ от р заранее задана, Это позволяет при решении задач о движении баротропной жидкости ограни­читься рассмотрением уравнения неразрывности и трех уравнений движения для нахождения четырех функций — v_x, v_y, v_z, р, а при исследовании равно­весия жидкости—рассмотрением трех уравнений (так как уравнение нераз­рывности удовлетворяется тождественно).

Жидкость, уравнение состояния которой имеет общий вид f(ρ,р,Т) = 0 и относительно которой не делается никаких специальных предположений (об изотермичности или адиабатичности процессов и др.), называют бароклинной. При решении задач о движении бароклинной жидкости приходится привле­кать уравнение энергии. Задача о равновесии жидкости, уравнение состоя­ния которой имеет общий вид f(ρ,р,Т) =0 и относительно которой не де­лается никаких специальных предположений, также не может быть точно ре­шена без использования уравнения энергии. Зависимость ρ от р в этом слу­чае заранее неизвестна и для каждой задачи может быть найдена только по­сле ее решения.

3. Равновесие тяжелой несжимаемой жидкости.

Главный вектор и главный момент сил давления на твердую поверхность. Равновесие тяжелой несжимаемой жидкости. Закон Архимеда.

Главный вектор и главный момент сил давления на твердую поверхность

Пусть имеется некоторое тело и пусть S — часть поверхности тела, соприкасающаяся с жидкостью, n — нормаль к элементу поверхности dS, направленная в ту сторону, где находится жидкость. На площадку dS со стороны жидкости дей­ствует сила

. (1.4.34)

Момент силы относительно начала координат

. (1.4.35)

Проинтегрировав (1.4.34) и (1.4.35) по поверхности S, получим об­щие формулы для главного вектора и главного момента сил, действующих на поверхность S со стороны жидкости:

(1.4.36)

(1.4.37)

Равновесие тяжелой несжимаемой жидкости. Закон Архимеда.

Для однородной несжимаемой жидкости уравнение равновесия можно записать в виде

, (1.4.38)

т.е. равновесие несжимаемой жидкости возможно только в потенциальном силовом поле. Пусть

F = - grad V. (1.4.39)

Тогда из (1.4.33) и (1.4.34) следует, что

, т.е.

. (1.4.40)

Постоянная интегрирования С находится из условия . Таким образом, найдено давление.

Если массовые силы – силы тяжести, то F_x = F_y = 0, F_z = - g и потенциал

V = gz. Из формулы (1.4.36) в этом случае получаем гидростатический закон

. (1.4.41)

Введем вместо z координату z′, положив

, т.е. будем отсчитывать z′ от так называемого приведенного уровня (p=0 при ). Тогда формула для давления примет вид

p = -ρg z′. (1.4.42)

Пусть в жидкость погружено тело. Поверхность этого тела S, объем τ. Вычислим главный вектор F^s и главный момент L сил, действующих со стороны жидкости на тело. Учитывая, что поверхность S замкнутая, находим проекции главного вектора

,

,

. (1.4.43)

Таким образом, на тело, погруженное в жидкость, действует сила, направленная снизу вверх и равная весу жидкости в объ­еме этого тела. Вычислим проекции главного момента.

,

,

.

Введем координаты центра тяжести объема

, .

Тогда выражения для L_x, L_y, L_z можно записать в виде

, ,. (1.4.44)

Формулы (1.4.43) решают задачу о нахождении момента.

Известно, что система сил приводится к одной равнодей­ствующей, если скалярное произведение главного вектора на главный момент равно нулю. В нашем случае это имеет место:

(F ·L) = F_XL_X + F_yL_y + F_zL_z = 0.

Выберем начало координат так, чтобы х₀ = y₀ = 0, т. е. чтобы ось z' проходила через центр тяжести объема. Тогда все со­ставляющие момента будут равны нулю.

Таким образом, система сил, действующих на тело, погру­женное в однородную несжимаемую жидкость, находящуюся в поле сил тяжести, статически эквивалентна одной силе, равной по величине весу жидкости в объеме тела и направленной вер­тикально вверх, причем линия действия этой силы проходит че­рез центр тяжести объема тела.

2. ОСНОВНЫЕ УРАВНЕНИЯ И ТЕОРЕМЫ ДИНАМИКИ ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА

1. УРАВНЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ.

1. Запись уравнений в форме Эйлера.

Система уравнений идеальной нетеплопроводной жидкости и постановка задач для нее. Уравнения Эйлера. Постановка задач об отыскании установившихся и неустановившихся течений идаельной жидкости.

Система уравнений идеальной нетеплопроводной жидкости и постановка задач для нее.

Будем предполагать, что жидкость идеальна, нетеплопровод­на и объемные источники тепла отсутствуют. Это означает, что τ_n = — пр,

t_x = t_y = t_z = О, ε = 0.

Уравнение неразрывности имеет вид

(1)

Уравнения движения идеальной жидкости (уравнения Эйлера) имеют вид

или

(2)

Уравнение энергии запишется в виде

(3)

Уравнение состояния

(4)

и выражение для внутренней энергии

(5)

Выпишем эти уравнения более подробно

,

,

,

,

,

.

Здесь .

Этой системе уравнений удовлетворяют все течения идеальной нетеплопроводной жидкости, как установившиеся, так и неустановившиеся, а также относящиеся к обтеканию жидкостью различных тел при разнообразных условиях.

При неустановившихся течениях жидкости гидродинамические функции зависят от координат и времени. Рассмотрим граничные условия для нестационарных течений.

1. Граничные условия на поверхности движущегося тела. В случае нестационарного течения тела могут перемещаться в жидкости, могут и изменять свою форму. Пусть S – поверхность обтекаемого тела, n – нормаль в точках S, v – скорость частиц жидкости, u(М,t) – скорость точки М поверхности тела в момент t.

- если S – поверхность непроницаемого тела;

- если тело проницаемое.

2. Граничные условия на поверхности раздела. В этом случае поверхность раздела может менять свою форму, перемещаясь с течением времени.

, , где- скорость точек поверхности, разделяющей жидкостиI и II.

3. Условия на бесконечности

, ,.

4. Начальные условия. Для нестационарных задач буду зависеть от того состояния, с которого оно началось.

, ,

Задача состоит в том, чтобы найти такие функции υ_x, υ_y, υ_z, p, ρ, T, которые являлись бы решениями системы уравнений гидромеханики.

Рассмотрим граничные условия для установившихся течений идеальной нетеплопроводной жидкости.

1. Граничные условия на поверхности тела.

- тело непроницаемо;

- тело проницаемо.

2. Условия на поверхности раздела жидкостей.

- жидкость движется вдоль поверхности , не проникая через нее.

- условие, относящееся к давлению на поверхности раздела.

3. Условия на бесконечности. Пусть некоторое тело обтекается потоком поступательным и однородным на бесконечности. В этом случае должны быть известны

, ,.

2. Различные формы записи уравнений движения.

Уравнения движения в натуральных координатах. Уравнение Эйлера в форме Громеко-Лэмба.

Уравнения Эйлера в форме Громеко-Лэмба

Выпишем уравнение Эйлера

. (1)

Введем в рассмотрение оператор и скалярное произведение

,

. (2)

Применим оператор к вектору скорости v и используем при записи вектора ускорения из уравнения (1). Уравнение Эйлера запишем в виде

(3)

Уравнение (3) – уравнение Эйлера в форме Громеки-Лэмба.

Запишем (3) в проекциях на оси, используя обозначение

,

,

.

Уравнения Громеки-Лэмба содержат в явном виде вектор вихря .

3. Адиабата Пуассона

Движение жидкости называется адиабатическим, если жид­кость не приобретает тепла извне и не отдает его. Предположе­ния, принятые в этом разделе (t = 0, ε = 0), означают, что мы рассматриваем адиабатические движения.

, (1)

где С – постоянная интегрирования, сохраняющая свое значение для движущейся частицы. Интеграл (1) называется адиабатой.

Рассмотрим газ, подчиняющийся уравнению Клапейрона

. (2)

Пусть с_υ и с_p – теплоемкость газа при постоянном объеме и постоянном давлении; предполагается, что они постоянны. В этом случае внутренняя энергия

. (3)

Учтем известное соотношение , и, выразивT из (2) через p и ρ, подставим Т в (3)

или (4)

Отношение называют показателем адиабаты.

(5)

Выражение (5) называют адиабатой Пуассона. Это соотношение имеет место в частице. Постоянная С может изменяться от частицы к частице.

2. ИНТЕГРАЛЫ УРАВНЕНИЙ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ

1. Интеграл Бернулли.

Функция давления. Интеграл Бернулли. Частные случаи интеграла Бернулли: однородная несжимаемая жидкость, идеальный газ.

Интеграл Бернулли. Частные случаи интеграла Бернулли

Предположим, что жидкость идеальна, массовые силы кон­сервативны,

движение установившееся, имеет место баротропность на линии тока.

Так как жидкость идеальна, то уравнение движения

. (1)

Так как массовые силы консервативны, то

F = - grad V

и уравнение (1) запишем

. (2)

Предположение о баротропности на линии тока означает, что

ρ = Ф(р,С), (3)

где С постоянна на линии тока

При установившемся движении траектории и линии тока совпадают.

Обозначим через dr(dx,dy,dz) элементарное пере­мещение вдоль линии тока и умножим скалярно все члены (2) на dr

(4)

Так как линия тока является и траекторий и grad V·dr = dV, grad p·dr = dp, перепишем выражение (4) в виде

(5)

Введем функцию P (p,C), имея ввиду (3)

(6)

С учетом (6) равенство (5) можно переписать в виде

(7)

Отсюда

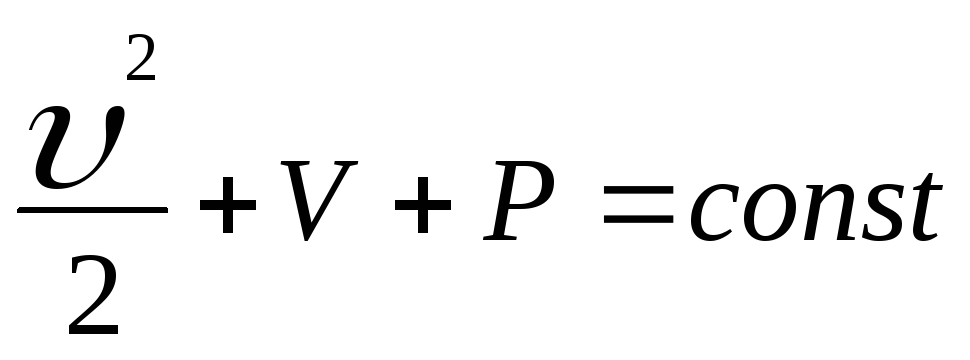(8)

Равенства (7), (8) имеют место на любой линии тока, но постоянная в правой части (8) может изменяться при переходе от одной линии тока к другой. Равенство (8) называют интегралом Бернулли.

Рассмотрим частные случаи интеграла Бернулли.

1. Однородная несжимаемая жидкость. В этом случае ρ – заданная постоянная и .

Интеграл Бернулли примет вид

. (9)

Если массовые силы — силы тяжести, то V = gz и интеграл Бернулли в этом случае

или (10)

Отдельные слагаемые в (10) имеют размерность длины и называются соответственно:

- скоростной,

z – геометрической,

- пьезометрической высотами.

Равенство (10) позволяет дать такую формулировку интеграла Бернулли: при движении однородной несжимаемой жидкости в поле сил тя­жести сумма скоростной, пьезометрической и геометрической высот постоянна вдоль линии тока.

2. Совершенный газ. В этом случае уравнение состояния есть уравнение

Клапейрона ,. Имеет место адиабата Пуассона. Введем новую постоянную.Тогда

, (11)

Вычислив Р(р) и подставив в (8), получим интеграл Бернулли в виде

(12)

Из физики известно, что производная равна квадрату скорости звука. В случае адиабатического процесса. Таким образом

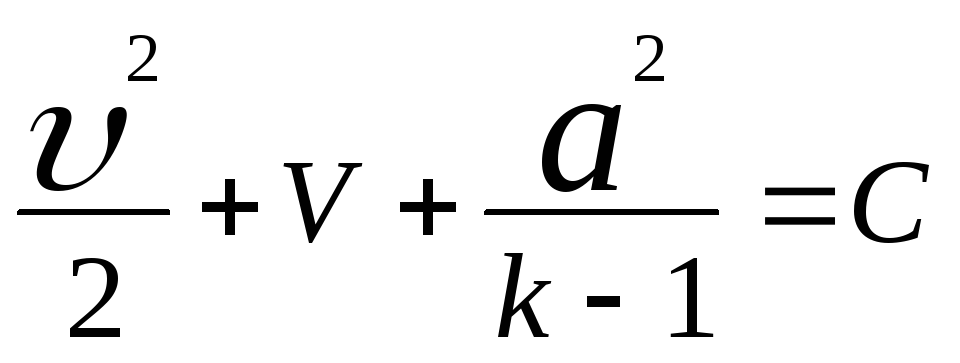(13)

Эта формула является одной из важных формул газовой ди­намики. В газовой динамике обычно массовые силы не учиты­вают, а постоянную С обозначают через i_o. В этом случае ин­теграл Бернулли принимает вид

(14)

Здесь υ – скорость газа, а – скорость звука в той же точке.

Здесь v — скорость газа, а — скорость звука в той же точке.

Чтобы определить постоянную в правой части (14), доста­точно знать характеристики в какой-либо одной точке линии тока. Из (14) следует, что скорость звука и температура, а с учетом (11), и давление и плотность будут максимальными на линии тока в точке, где скорость равна нулю. Эти величины обычно обозначают через а₀, Т₀, р_о, ρ_о и называют параметрами адиабатически заторможенного газа (параметрами торможе­ния). Величину

называют энтальпией (теплосодержанием).

Соответственно i₀ называют энтальпией торможения.

2. Интегрирование уравнений движения.

Интеграл Лагранжа. Интеграл Эйлера-Бернулли.

Интеграл Лагранжа

Сделаем предположения: 1) жидкость идеальна; 2) имеется баротропность

во всем пространстве, занятом жидкостью, т. е. ρ = Ф(р); 3) массовые силы консервативны; 4) движение без­вихревое.

Для безвихревого движения идеальной жидкости уравнение Эйлера в форме Громеки-Лэмба принимает вид

(1)

Так как жидкость баротропна, то может быть введена функция

(2)

(3)

Предположение 3) означает, что

F = -grad V. (4)

Из предположения 4) следует, что

, (5)

Подставляя (3), (4), (5) в (1), получаем

(6)

Из равенства (6) следует, что выражение в скобках на зависит от координат, но может зависеть от времени

(7)

Полученное соотношение носит название интеграла Лагранжа.

Сравним интеграл Лагранжа и интеграл Бернулли. Как мы видели, уравнение Эйлера при соответствующих условиях при­водит к этим интегралам. Интеграл Лагранжа в некотором смысле более общий, чем интеграл Бернулли, так как годится и для неустановившихся движений. Но он менее общий в том смысле, что требует безвихревого движения и полной баротроп­ности (в интеграле Бернулли достаточно баротропности только на линии тока). Область действия этих интегралов разная.

Интеграл Эйлера-Бернулли

Предположим, что жидкость идеальна, баротропна, массовые силы имеют потенциал, движение безвихревое и установившее­ся. Первые четыре предположения позволяют написать интеграл Лагранжа

(1)

Так как движение установившееся, то v_x, v_y, v_z, а следователь­но, и φ не зависят от времени, т. е. φ = φ (х, у, z). Тогда вы­падает из (1), иf(t) переходит в постоянную. Имеем

(2)

Интеграл (2) носит название интеграла Эйлера — Бернулли. Здесь постоянная С одна и та же для всего потока в отличие от интеграла Бернулли, в котором постоянная С на разных линиях тока различна.

2. ПЛОСКИЕ БЕЗВИХРЕВЫЕ ТЕЧЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ И ГАЗА

1. Условия существования безвихревых течений.

Плоские безвихревые установившиеся течения идеальной несжимаемой жидкости.

Течение называется плоским, если все частицы движутся па­раллельно некоторой плоскости, причем скорости частиц в соот­ветствующих точках плоскостей, параллельных этой фиксиро­ванной плоскости, одинаковы по величине и направлению. Очевидно, в этом случае достаточно рассмотреть течение в од­ной плоскости, которую можно принять за плоскость (х, у).При таком выборе системы координат все величины будут зависеть только от координат х, у. Это означает, что υ_z = 0, . Так как течение

предполагается установившимся, то. Сле­дует иметь в виду, что, говоря

о течении в плоскости, мы фак­тически рассматриваем течение в слое между плоскостью (х, у) и ей параллельной. Так, например, обтеканию контура в пло­скости (х, у) соответствует в пространстве обтекание цилиндра, для которого контур в плоскости (х, у) является направляющей.

Так как жидкость несжимаема, то плотность постоянна и должна быть известна: р = ро. Искомые функции

v_x = v_x(x, у), v_y = v_y(x, у), р = р{х,у), Е==Е{х, у). (1)

Уравнениями плоской задачи являются уравнение неразрыв­ности, уравнения Эйлера в проекциях на оси х и у и уравнение энергии. Для несжимаемой жидкости уравнение неразрывности будет иметь вид

(2)

Будем считать, что массовые силы консервативны или отсутст­вуют. Тогда при предположениях, сделанных в данной главе, справедлив интеграл Эйлера — Бернулли. Поэтому вместо урав­нений Эйлера используем условие отсутствия вихря и интеграл Эйлера — Бернулли.

Условие отсутствия вихря rot v = 0 для плоского движения, когда , приводит к равенству

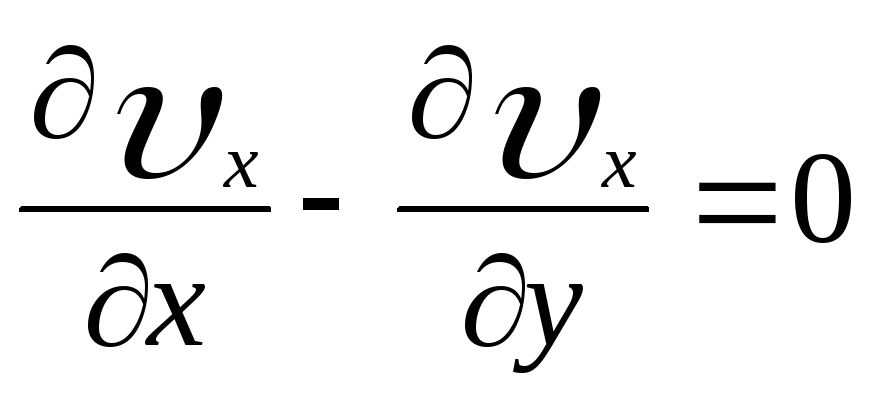(3)

Интеграл Эйлера –Бернулли имеет вид

(4)

Уравнение энергии для несжимаемой жидкости. Если нет притока тепла, дает

(5)

т. е. для несжимаемой жидкости энергия в частице сохраняется. Уравнения (2), (3) содержат лишь функции v_x и v_y. Уравнение (4) может быть использовано для нахождения дав­ления, если известны скорости v_x и v_y.

Условие отсутствия вихря имеет вид

(6)

Вследствие чего существует функция φ(x,y), такая, что

(7)

, . (8)

Потенциал скоростей несжимаемой жидкости, как уже было по­казано и ранее, в силу уравнения неразрывности (2) удовле­творяет уравнению Лапласа

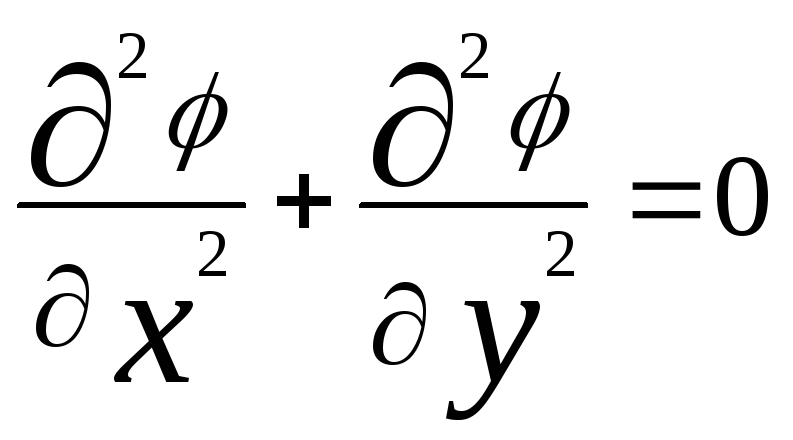(9)

Решение уравнения (9) должно удовлетворять граничным условиям. В случае обтекания тел однородным безграничным потоком решение должно быть таким, чтобы на бесконечности скорость потока была равна заданной величине V∞, а на поверх­ности S тела было удовлетворено условие обтекания, т. е.

, ,(10)

Задача нахождения решения уравнения Лапласа по заданному значению нормальной производной на границе называется зада­чей Неймана. В случае, если область бесконечна, имеем внеш­нюю задачу Неймана с граничными условиями в виде (10).

Из уравнения неразрывности следует

(11)

Равенство (11) – условие того, что дифференциальная форма есть полный дифференциал некоторой функции ψ(x,y) и, следовательно,

, . (12)

Выпишем уравнение линии тока для плоского случая

(13)

(14)

Видим, что dψ=0, ψ=const.

2. Комплексный потенциал.

Комплексный потенциал. Комплексные потенциалы простейших потоков.

Мы получили выражения для проекций скорости через производные от функций φ и ψ. Сравнивая их, получаем уравнения связи между потенциалом скоростей и функцией тока

, . (1)

Это известные из теории функций комплексного переменного условия Коши — Римана, которые гарантируют, что функция

будет функцией одной комплексной переменной z = x + iy. Функцию (2)

Называют комплексным потенциалом, или характеристической функцией течения. Если комплексный потенциал известен, то легко найти функции φ и ψ.

, (3)

Введение комплексного потенциала позволяет применить хоро­шо разработанный аппарат теории функций комплексного пере­менного для отыскания решения многих задач об установив­шихся плоских потенциальных течениях идеальной несжимаемой жидкости.

Рассмотрим комплексные потенциалы простейшего вида и установим, каким течениям они соответствуют.

Пример 1. ω (z) = az, где а > 0 (вещественно):

φ (х, у) + iψ (x, у) = а(х + iy).

Отделим вещественную и мнимую части

φ (х, у) = ах, ψ (х, у) = ау.

Компоненты скорости

,

Имеем течение вдоль оси х с постоянной скоростью а. Линии тока ψ = const есть прямые у = const, линии равного потен­циала φ = const есть х = const.

Пример 2. ω (z) = ae~^iaz, где а и α вещественны и пусть, для определенности, положительны. Имеем

Отсюда

,

.

Компоненты скорости

, .

Линии тока ψ=const есть прямые y=tgαx+C, образующие угол α с осью x. (рис.3)Это же следует и из выражения для скоростей. Таким образом, имеем поступательный поток с постоянной скоростью, образующий угол αс осью x. Линии φ=const – прямые, перпендикулярные линиям тока.

рис. 3

Пример 3. , гдеq вещественно.

Рассмотрение этого примера удобнее вести в полярных координатах r,θ

, , , , , .

Линии тока ψ = const будут лучами, выходящими из начала координат. Линии равного потенциала φ = const есть окружно­сти r = const (рис. 4).

рис.4

Пример 4. Пусть в точке А плоскости {х, у) расположен источник обильности q, в точке В — источник обильности —q (сток), причем комплексные координаты точек (рис. 5)

, .

рис. 5

Комплексный потенциал течения, вызываемого каждым из ис­точников, имеет вид

, .

Комплексный потенциал суммарного течения

,

.

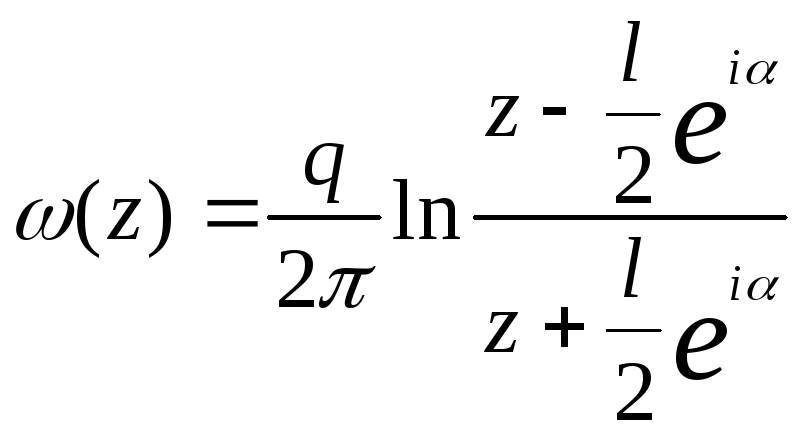Пусть l→0, а q→∞, причем так, чтобы произведение ql оставалось постоянным: ql=M. Тогда для такого предельного течения комплексный потенциал будет иметь вид

Эта формула дает комплексный потенциал течения от расположенного в начале координат диполя с моментом М и осью диполя, образующей угол α с осью x. Ось диполя принято направлять от стока к источнику.

Вихревые движения идеальной жидкости.

Мы будем рассматривать вихревые движения, т. е. такие движения, у которых вектор вихря во всех точках области или какой-либо ее части не равен нулю: .

При изучении вихревых движений приходится иметь дело с такими понятиями, как циркуляция скорости и поток вектора вихря скорости через поверхность. Из теоремы Стокса следует, что поток вихря через поверхность S равен циркуляции скоро­сти по контуру, ограничивающему эту поверхность:

.

Таким образом, циркуляция является одной из важных харак­теристик вихревых течений.

Теорема Томпсона.

Прежде чем сформулировать и доказать теорему Томсона, рассмотрим один вспомогательный результат кинематического ха­рактера. Обратим внимание на то, как с течением времени изменяется цир­куляция скорости Г, вычисляемая по контуру, состоящему все время из одних и тех же частиц жидкости (так называемому «жидкому» контуру). Такой контур перемещается вместе с жид­костью и может деформироваться. Очевидно, что для жидкого контура Г = Г(t).

Если кривая замкнута (А = В), то

(1)

Таким образом, производная по времени от циркуляции скоро­сти по замкнутому (жидкому) контуру равна циркуляции уско­рения по тому же контуру.

Применим полученный нами результат для доказательства так называемой теоремы Томсона: если жидкость идеальна, баротропна и массовые силы имеют потенциал, то циркуляция скорости по любому замкнутому жидкому контуру не зависит от времени.

Для идеальной жидкости имеем

. (2)

Так как жидкость баротропна (ρ = ρ(р)), то существует функ­ция P(p) такая, что . Так как массовые силы консервативны,

F = - grad V. Поэтому, учитывая условия Теоремы Томпсона, будем иметь

. (3)

Подставляя (3) в (1), получим

, (4)

откуда Г(t) = const.

Таким образом, циркуляция скорости по любому замкнутому контуру, движущемуся вместе с жидкостью, остается для этого контура постоянной во все время движения.

Замечание. Поскольку из теоремы Стокса следует, что поток вихря через поверхность S равен циркуляции скорости по контуру, ограничивающему эту поверхность, то из теоремы Томпсона вытекает, что поток вектора вихря через поверхность S, ограниченную жидким контуром, не зависит от времени.

Теорема Лагранжа.

Пусть выполнены условия теоремы Томсона, т. е. жидкость идеальна, баротропна и массовые силы консервативны. Тогда справедлива следующая теорема Лагранжа: если в некоторый момент времени t₀ в фиксированной массе жидкости нет вих­рей, то их не было в предыдущие и не будет в последующие моменты времени.

Действительно, пусть в рассматриваемой массе жидкости, находящейся в объеме τ, в момент времени t₀ нет вихрей, т. е. Ω = 0. Тогда течение жидкости потенциально: v = grad φ и цир­куляция скорости Г_о по произвольному замкнутому контуру l₀ равна нулю

(1)

Рассмотрим выделенную массу жидкости в любой другой мо­мент времени t и в ней возьмем произвольный контур l. Лю­бому контуру l в момент t можно сопоставить контур l₀ в мо­мент t₀, состоящий из тех же частиц жидкости, для которого справедлива формула (1).

По теореме Томсона циркуляция Г по контуру l будет также равна нулю. Применяя формулу Стокса, получаем для любого момента времени

(2)

где S — поверхность, ограниченная контуром l и целиком находящаяся в объеме, занимаемом жидкостью.

Поскольку для любой области S интеграл равен нулю, из (2) следует, что Ω = 0. Теорема Лагранжа составляет основу для рассмотрения безвихревых течений в гидромеханике идеаль­ной жидкости, так как если движение жидкости безвихревое (потенциальное) в начальный момент времени, то оно будет безвихревым (потенциальным) и в последующие моменты вре­мени.

Все предположения в теореме Лагранжа существенны. В частности, существенно не сформулированное явно предполо­жение о гладкости поля скоростей.

В условиях Земли теорема Лагранжа является приближен­ной, так как массовые силы будут консервативны, если не учи­тывать силы Кориолиса, а сжимаемую жидкость можно рас­сматривать как баротропную, если пренебречь рядом факторов, например, теплопроводностью и др.

Теорема Гельмгольца о сохранении вихрей

Предполагаются выполненными условия теоремы Томсона, а именно: жидкость идеальна, баротропна и массовые силы консервативны.

Первая теорема. Если жидкие частицы в какой-либо момент времени t₀ образуют вихревую линию, то эти же частицы обра­зуют вихревую линию во все последущие и все предыдущие моменты времени.

Докажем сначала, что если в некоторый момент времени жидкие частицы образут вихревую поверхность, то эти же час­тицы образуют вихревую поверхность при всех t (t <t₀ и t>t₀).

В каждой точке вихревой поверхности согласно ее опреде­лению вектор вихря скорости перпендикулярен нормали к по­верхности, т. е.

(1)

Пусть жидкие частицы в момент t_о образуют вихревую поверхность S_o. Рассмотрим на этой поверхности произвольный замк­нутый контур l₀, ограничивающий участок поверхности σ_о. Со­гласно формуле Стокса имеем

(2)

В момент времени t частицы жидкости, находившиеся в момент t₀ на контуре l₀, образуют контур l, ограничивающий площадку σ поверхности S, на которую перешли частицы с поверхности So. Но по теореме Томсона циркуляция по жидкому контуру не ме­няется со временем, т. е.

Следовательно, для участка σ поверхности S, учитывая формулу Стокса, получаем

(3)

Ввиду произвольности σ из (3) следует, что в любой точке поверхности выполняется (1), т. е. поверхность S вихревая. Действительно, допустим, что это не так и поверхность не вих­ревая, тогда найдется такая точка А этой поверхности, в кото­рой . По непрерывностии в некоторой области,ограничивающей эту точку. Эту область можно выбрать на­столько малой, что Ω_n будет сохранять тот же знак, что и в точ­ке А. Взяв эту область за σ, получим , что противоречит (3).

Докажем теперь, что вихревая линия остается при движении жидкости вихревой. Пусть в момент времени t₀ жидкая кри­вая А₀В₀ есть вихревая линия. Проведем через какую-либо точку этой линии две пересекающиеся кривые. Проведя через точки этих кривых вихревые линии, получим вихревые поверх­ности S₁⁰⁾ и S₂⁰⁾. Линия пересечения S⁽₁⁰⁾ и S₂⁰⁾ есть по построе­нию вихревая линия А_аВ₀. В момент времени t жидкие поверх-

ности S⁽₁⁰⁾ и S₂⁰⁾ перейдут в поверхности S₁ и S₂. По доказанному выше поверхности S₁ и S₂ будут вихревыми. На поверхности S₁ будут все жидкие частицы, которые были на S₁, на S₂ — все частицы, которые были на S₂⁰⁾. Жидкие частицы, которые при­надлежали сразу двум поверхностям S⁽₁⁰⁾ и S₂⁰⁾ опять будут принадлежать сразу двум поверхностям S₁ и S₂. Это значит, что вихревая линия А₀В₀ перешла в линию пересечения АВ вихревых

поверхностей S₁ и S₂.

Вектор вихря Ω в любой точке пересечения двух поверхно­стей S₁ и S₂ должен лежать в касательной плоскости к каждой из поверхностей, т. е. вектор Ω направлен по касательной к линии пересечения АВ, поэтому линия АВ - вихревая линия.

Вторая теорема. Интенсивность вихревой трубки постоянна по ее длине и не изменяется со временем.

Совокупность вихревых линий, проведенных через замкнутый контур, образует вихревую трубку. Интенсивностью вихревой трубки называют циркуляцию скорости по контуру, охватывающему трубку .

Такое понятие имеет смысл, если ин­тенсивность (т. е. циркуляция Г) не зависит от положения кон­тура l по длине трубки. По теореме Стокса

, где σ- поверхность, пересекающая вихревую трубку.

Докажем, что для всех контуров l, лежащих на поверхности трубки и охватывающих ее, интенсивность одна и та же. Пусть l₁ и l₂ — два каких-либо из таких контуров. Рассмотрим объем τ, ограниченный поверхностью S, состоящий из S₁, Σ, S₂, где S₁ и S₂ — сечения трубки, ограниченные соответственно контурами l₁ и l₂, а Σ — часть боковой поверхности трубки, заключенная между l₁ и l_2.

Рассмотрим поток вихря через поверхность S. Согласно теореме Гаусса-Остроградского получим

(4)

(5)

Поскольку на поверхности Σ (вихревая поверхность) имеем

(6)

Здесь n — внешняя нормаль к поверхности, ограничивающей объем τ . Введя и используя формулу Стокса, получим

,

, (7)

Где Г₁ и Г₂ – циркуляции, вычисленные при обходе контуров l₁ и l₂ в одном направлении. Из (6), учитывая (7), получим

, Г₁= Г₂,

т. е. интенсивность Г вихревой трубки постоянна по ее длине. Так как выполнены условия теоремы Томсона, то циркуляция по любому жидкому контуру не зависит от времени и, следова­тельно, интенсивность вихревой трубки не изменяется со вре­менем.

Уравнение Фридмана для вихря.

. (1)

Уравнение (1) называется уравнением Фридмана. Если поле массовых сил консервативно (F = —grad V) и жидкость баротропна, то

rotF = 0, gradρX grad р = φ'(р) grad pX grad p = 0.

В этом случае уравнение Фридмана приобретает вид

(2)

Если, кроме того, жидкость несжимаема, уравнение (1) запишется в виде

(3)

Уравнения (2), (3) впервые были получены Гельмгольцем. Теоремы Гельмгольца можно доказать исходя из уравнения (2).

Уравнение Фридмана дает возможность количественно описать изменение вихря, происходящее вследствие неконсервативности массовых сил и бароклинности жидкости.

Образование вихрей. Теорема Бьеркнеса об ускорении циркуляции.

Теорема Лагранжа о безвихревом движении жидкости и тео­рема Гельмгольца о сохранении вихрей справедливы при пред­положениях, что жидкость идеальна, баротропна и массовые силы консервативны. В этом параграфе будет показано, что если жид­кость не баротропна или массовые силы не консервативны, то вихри даже в идеальной жидкости могут возникать и уничто­жаться. При доказательстве теоремы Томсона было получено равенство

Учитывая уравнения Эйлера, описывающие движение идеальной жидкости, получим

(1)

Рассмотрим два случая: 1) жидкость баротропна: ρ = φ(р), но массовые силы не консервативны; 2) жидкость бароклинна, т. е. плотность зависит не только от давления, но и от других параметров, например, температуры, влажности (для воздуха) или от солености (для воды).

В первом случае равенство (1) принимает вид

(2)

Но правая часть (2)— работа силы, действующей на единицу массы, при обходе контура l. Эта работа в неконсервативном поле, вообще говоря, не равна нулю. Следовательно, и теорема Томсона несправедлива, вихри могут возникать и мо­гут уничтожаться

Рассмотрим второй случай, предполагая, что массовые силы консервативны: F = —grad V, но жидкость бароклинна. В этом случае равенство (1) принимает вид

(3)

где .

Рассмотрим два семейства поверхностей: р = const (изоба­рические поверхности) и ω = const (изостерические поверхно­сти). В баротропной жидкости плотность сохраняет постоянное значение на изобарической поверхности. Следовательно, в баротропной жидкости изобарические и изостерические поверхности совпадают. В рассматриваемом случае эти поверхности будут пересекаться. Четыре поверхности образуют трубку, которая называется изобаро-изостерической.

Рассмотрим трубку, для которой ,, и контурABCD, охватывающий эту трубку (рис. 6). Тогда

(4)

При другом расположении поверхностей можно получить равен­ствоВ первом случае трубка называется единичной отрицательной, а во втором — единичной положительной изоба­ро-изостерической трубкой. Если контур охватываетN⁺ единич­ных положительных трубок и N^-отрицательных, то

. (5)

Равенства (3), (5) составляют содержание теоремы Бьеркнеса. Они показывают, что в бароклинной жидкости ,и, следовательно, вихри в бароклинной жидкости могут возни­кать и уничтожаться.