8. Подобие гидромеханических процессов.

Подобие течений вязкой жидкости. Сходственные пространственно-временные точки.

Два физических явления называют подобными, если величины, характеризующие одно явление, могут быть получены из соответствующих величин другого, взятых в сходственных пространственно-временных точках, простым умножением на одинаковые во всех точках множители, называемые коэффициентами подобия.

Рассмотрим подобие течений вязкой жид­кости, находящейся в поле силы тяжести, в предположении, что коэффициент вязкости μ постоянен. Вопрос о подобии имеет значение и при рассмотрении теоретических вопросов, и особен­но при экспериментальных исследованиях. В частности, нужно знать те условия, при выполнении которых результаты экспери­ментальных исследований над моделями можно переносить на реальные объекты.

Рассмотрим два течения вязкой жидкости с разными коэф­фициентами вязкости около двух геометрически подобных тел.

Пусть а₁, а₂ — характерные размеры первого и второго тел. Движение вязкой жидкости с коэффициентом вязкости ν₁ около первого тела будем описывать с помощью переменных х₁, у₁, z₁, t₁. Аналогично движение вязкой жидкости с коэффициентом вяз­кости ν₂ около второго тела будем описывать с помощью пере­менных x₂, y₂, z₂, t₂. Так как размерность коэффициента вязко­сти , то величина— имеет размерность времени: Величины a₁ и а₂ определяют естественный линейный масштаб в первой и второй задачах, величины имогут быть приняты соответственно за масштабы времени. Имея это в виду, введем безразмерные координаты и время для каж­дого течения с помощью соотношений

Сходственными пространственно-временными точками для двух течений около геометрически подобных тел будем называть точки (xi, yi, zi, ti), для которых безразмерные координаты и безразмерные времена одинаковы, т.е. точки, для которых

, ,,,

или, что то же самое,

, ,,.

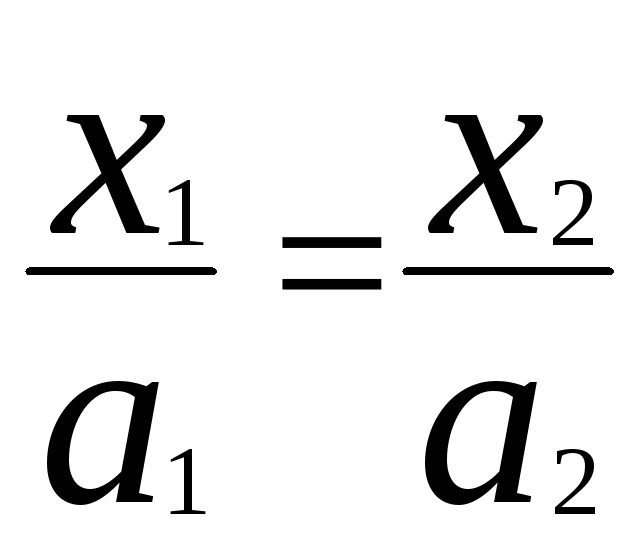В безразмерных координатах рассматриваемые геометрически подобные тела будут иметь характерный размер, равный еди­нице, и оба тела будут геометрически тождественны.

Запись уравнений гидромеханики вязкой жидкости в безразмерном виде

Имеем систему уравнений вязкой жидкости

,

. (1)

Предположим, что вектор g массовых сил постоянен в простран­стве и времени. Обозначим через а характерный размер рас­сматриваемого течения (например, хорду или размах крыла) и введем вместо х, у, z, t безразмерные координаты и время по формулам

, ,,. (2)

Введем безразмерные функции

, ,. (3)

Будем теперь рассматривать u, П, y как функции безразмер­ных переменных ξ, η, ζ, τ. Заменим в уравнениях (1) коорди­наты х, у, z на ξ, η, ζ и время t на τ по формулам (2). Заме­ним в этих же уравнениях величины v, иg на u, П и по формулам (3). Сокращая на общий множительиз (1) получаем систему уравнений

,

,

где . (4)

Система (4)—система уравнений вязкой жидкости, запи­санная для безразмерных функций в безразмерных независи­мых переменных (безразмерная форма уравнений Навье — Стокса). Систему (4) можно записать в виде

,

,

Имея в виду, что операторы , Δ,div относятся к переменным ξ, η, ζ, τ.

Критерии подобия. Числа Рейнольдса, Фруда, Струхаля, Эйлера.

Два течения вязкой жидкости (первое и второе) будем на­зывать подобными, если значения соответственных гидродинами­ческих величин, вычисленные для сходственных пространствен­но-временных точек, отличаются лишь некоторыми постоянными множителями. Эти множители могут быть разными для различ­ных гидродинамических величин (один для скорости, другой для давления).

Пусть имеем два течения около геометрически подобных тел. Пусть они характеризуются величинами

, ,,,

, ,,,. (1)

Для каждого из этих движений можем выписать безразмерную систему уравнений

,

(2)

Решения систем (2), если иметь в виду внешние задачи об об­текании тел, должны удовлетворять условиям прилипания на границах S₁ обтекаемых тел (S₁ — поверхность тела с характер­ным размером, равным единице) и условиям на бесконечности

, . (3)

Так как безразмерные искомые величины иотличают­ся от размерных искомых величин постоянными множителями,то для подобия движений достаточно, чтобы в сходственных пространственно-временных точках имели место равенства

, (4)

Так как краевая задача об отыскании величин иста­вится для одинаковых областей, для которых характерный раз­мер равен единице, при одинаковых условиях на границе обте­каемых тел, для выполнения (4) достаточно, чтобы:

1. уравнения (2) для течения 1 (i = 1) и для течения 2 (i = 2) совпадали;

2. условия на бесконечности были одинаковы, т. е.

, (5)

ибо тогда обе краевые задачи будут тождественны.

Для совпадения уравнений необходимо, чтобы

, (6)

что дает следующее равенство:

, (7)

Условия (5), записанные в размерных величинах, приводят к соотношению

. (8)

Равенства (7) и (8) и являются условиями, достаточными для подобия течений. Как видно, они носят векторный характер. Из этого следует, что для выполнения (7) необходимо, чтобы векторы g₁ и g₂ были параллельны: g₁ || g₂; для выполнения (8)—чтобы были параллельны скорости на бесконечности: . Если считать, что эти условия параллельности вы­полнены, то из (7) и (8) получаем

, (9)

. (10)

Если (9) возвести в квадрат и разделить на (10), то будем иметь

. (11)

Условия (9), (11) эквивалентны условиям (9), (10). Безразмерную величину

называют числом Рейнольдса, безразмерную величину

называют числом Фруда.

Таким образом, два установившихся течения около геомет­рически подобных тел будут подобны, если выполнены следую­щие четыре условия:

1) , 3),

2) g₁ || g_2, 4) , (12)

где числа Re и Fr вычисляются по скоростям на бесконечности. Обычно условия 1) и 2) подразумеваются выполненными, и тогда условия подобия записываются в виде

, . (13)

Заметим, что число Re содержит коэффициент . Этот параметр подобия характерен для вязкой жидкости. В идеальной жидко­сти= 0 иRe = ∞. Подобие же по числу Фруда имеет смысл как для вязкой, так и для идеальной жидкости.

Следует отметить следующие безразмерные комплексы («числа подобия»):

- число Струхаля,

- число Эйлера,

- число Рейнольдса,

- число Фруда,

где соответственно время, длина ( в частности, координат), скорость, давление и объемные силы.

Среди всех чисел подобия особо выделим составленные только из тех масштабов сравниваемых потоков и физических констант среды, которые заключаются в постановке задачи об определении движения, т.е. наперед заданы. Одинаковость таких чисел подобия обуславливает подобие двух сравниваемых течений, и поэтому сами числа могут быть названы критериями подобия. Критериев подобия на самом деле меньше, чем чисел подобия для соответствующего класса течений, так как не все масштабные величины, введенные при составлении безразмерных уравнений и граничных и начальных условий, на самом деле могут быть заданы наперед. Значения некоторых из них определяются только после того, как будет получено единственное решение данной конкретной задачи.

Течение вязкой жидкости при больших числах Рейнольдса. Пограничный слой.

Различая движения вязких жидкостей по характерным для этих движений рейнольдовским числам, можно выделить два крайних, обладающих существенными особенностями случая: движение с малыми рейнольдовскими числами и движения с большими рейнольдовскими числами.

Течениям идеальной жидкости отвечает число Re = ∞. Если числа Рейнольдса велики (Re >> 1), то можно ожидать, что те­чения вязкой жидкости близки к течениям идеальной. Это тем более вероятно, что решение задачи о потенциальном течении идеальной жидкости является точным решением уравнений вяз­кой жидкости. Однако, как было показано ранее, потенциаль­ные решения не обеспечивают выполнения граничных условий на поверхности обтекаемого тела. Поэтому, если рассматривать обтекание некоторого тела, то следует ожидать, что течения вязкой жидкости при больших числах Re будут близки к тече­ниям идеальной жидкости всюду, за исключением тонкого слоя

рис.7

около границы. В этом тонком слое влияние вязкости суще­ственно сказывается на распределении скорости. Гипотезу о су­ществовании такого тонкого переходного слоя подтверждают и эксперименты. Этот тонкий слой принято называть пограничным.

Возникает вопрос, как определить его толщину? Конечно, толщина пограничного слоя — понятие очень условное. Практически толщиной пограничного слоя называют такое рас­стояние от поверхности тела, на котором касательные состав­ляющие скорости вязкого и идеального течений жидкости от­личаются на пренебрежимо малую величину. Таким образом, область потока, обтекающего тело, можно разделить на две — область пограничного слоя (I) и область вне его (II) (рис. 7). В пограничном слое рассматривают дви­жение вязкой жидкости в предположении, что отношение (— характерный размер). Последнее соотношение позволяет значительно упростить уравнения движения вязкой жидкости. В областиII, вне пограничного слоя, принимают, что течение совпадает с потенциальным течением идеальной жидкости.

Схему описания пограничного слоя предложил в 1904 г. Прандтль.

Будем считать, что Re >> 1. Упростим уравнения движения вязкой жидкости применительно к пограничному слою, поль­зуясь тем, что . Течение жидкости предполагаем лами­нарным.

Рассмотрим задачу об обтекании некоторого контура пло­ским потоком вязкой жидкости. Положение точки в погранич­ном слое можно определить, задавая длину х дуги, отсчитывае­мую от точки разветвления потока, и расстояние у по нормали от контура. Так как толщина пограничного слоя весьма мала по сравнению с радиусом кривизны, то, пренебрегая кривизной контура, можно в пределах слоя рассматривать х и у как пря­моугольные декартовы координаты. Если внешних сил нет, то движение жидкости описывается системой уравнений

, (1)

, (2)

. (3)

Будем рассматривать течение внутри слоя , где— толщина пограничного слоя. Предположим

. (4)

Составляющая v_x на внешней границе пограничного слоя имеет порядок V, где V — скорость на бесконечности. Предпо­ложим, что это справедливо во всем пограничном слое, т. е..

υ_x = 0(V). (5)

При изменении х от нуля до l скорость меняется на величину порядка V, поэтому

, . (6)

При изменении у от 0 до скоростьυ_x меняется от нуля (на стенке) до величины порядка V, поэтому

, . (7)

В силу предположения (4) , поэтому уравнение (1) приобретает вид

. (8)

В силу (5), (6) имеем

.

Порядок величины υ_у можно оценить, используя уравнение неразрывности

, .

Следовательно, .

Если дополнительно предположить, что рассматриваются только такие нестационарные течения, для которых имеет тот же порядокили меньше, то левая часть уравненияимеет порядок.

Прандтль предположил, что в пограничном слое силы инер­ции и силы вязкого трения одного порядка. Принимая это пред­положение, получим, что

или, учитывая (7),

.

Отсюда следует, что

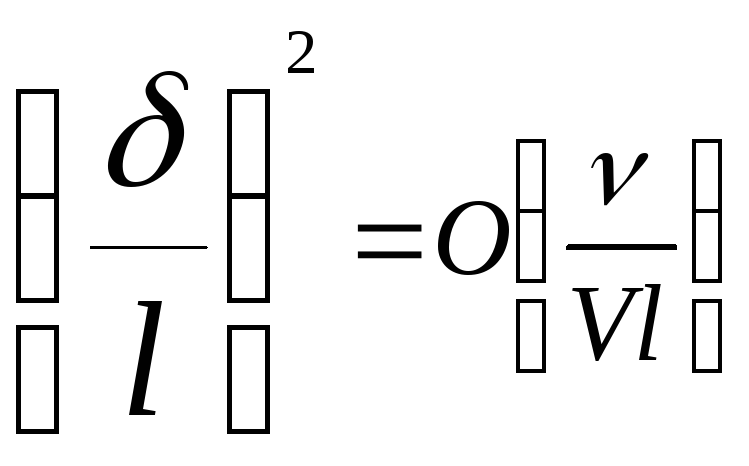, . (9)

Относительная толщина пограничного слоя обратно пропорцио­нальна (так называемый первый результат теории погра­ничного слоя). Чем больше числоRe, тем тоньше пограничный слой.

Для оценки члена используем следующие сообра­жения. На внешней границе пограничного слоя при устано­вившемся течении справедлив интеграл Бернулли

.

Отсюда

. (10)

Этот результат мы имеем и из уравнения (8).

Рассмотрим теперь уравнение (2). Имеем

, ,

, . (11)

Очевидно, в слагаемоеможно отбросить по сравнению с. Воспользовавшись оценкой (9), получим

. (12)

Из (11), (12) и уравнения (2) следует, что

. (13)

Из сравнения (13) с (10) следует, что в пограничном слое

.

Таким образом, давление по оси у меняется существенно медленнее, чем по оси х, поэтому уравнение (2) можно заме­нить уравнением

, . (14)

Давление поперек пограничного слоя не меняется.

Система уравнений вязкой жидкости содержит еще уравнение

неразрывности. Оно остается без изменений.

Уравнения (8), (3), (14) образуют систему уравнений пограничного слоя

,

,

. (15)

Последнее из уравнений (15) означает, что давление через по­граничный слой по нормали передается без изменения. Так как вне пограничного слоя жидкость можно считать идеальной, дав­ление может быть взято из решения уравнений идеальной жид­кости. Но так как пограничный слой тонок, то можно считать, что во всем пограничном слое зависимость давления р от х и t такая же, как в идеальной жидкости. Тогда два первых уравне­ния (15) можно рассматривать как систему уравнений погра­ничного слоя для функций υ_x и υ_y, в которых известная функция, найденная из решения задачи обтекания тела пото­ком идеальной жидкости.

Если течение установившееся, то вне пограничного слоя (идеальная жидкость) справедлив интеграл Бернулли

, . (16)

Если и = U — скорость на внешней границе пограничного слоя, то в силу

того, что не изменяется поперек пограничного слоя (не зависит от y),

уравнения пограничного слоя с учетом (16) можно записать в следующем виде:

,

. (17)

Так как, в частности, при , то за

функцию U может быть взято решение уравнений идеальной жидкости при

у = 0. При этом U = U_x и зависит только от х. Искомые функции υ_x, υ_y нужно находить как решение уравне­ний (17) при следующих граничных условиях:

1) на теле при 0 ≤ x ≤ (условия прилипания)

, (18)

2) на внешней границе пограничного слоя

υ_x = (1-ε) U (х), (19)

где ε — заданная малая величина.

Фактически ввиду неопределенности границы пограничного слоя ( неизвестна) соотношение (19) не является гранич­ным условием, так как в нем υ_x = υ_x {х, (х)), где неиз­вестна.

Поэтому граничные условия несколько видоизменяют. Во-первых, решения системы (17) можно найти только при за­данном значении υ_x при

х = 0. Во-вторых, условие на границе пограничного слоя заменяют условием при исходя из предположения, что внутри пограничного слоя быстро стремится к предельным значениям при удалении от тела. Таким образом, вместо условий (18), (19) получают условия:

1) при ,,

2) ,

3) . (20)

Имея распределение скоростей в пограничном слое, т.е. найдя решение уравнений (17), удовлетворяющее условиям (20), можно найти внешнюю границу слоя , используя (19):

. (21)

Течение вязкой жидкости при малых числах Рейнольдса. Для установивше­гося течения вязкой жидкости существенно значение числа Рей­нольдса, причем при отсутствии массовых сил (g = 0) число Re является единственным параметром, характеризующим с точностью до подобия рассматриваемое течение. Поэтому когда не удается найти точное решение задачи, в общем случае раз­вивают приближенные методы, соответствующие тем или иным предположениям относительно числа Рейнольдса. Такие при­ближенные методы развиты в предположении, что Re >> 1 и Re << 1.

Рассмотрим течения вязкой жидкости при ма­лых числах Рейнольдса

Re << 1. Это означает, что к рассматри­ваемому виду относятся медленные движения вязкой жидкости, движения жидкости с большой вязкостью, движения малых тел в сравнительно вязких жидкостях.

Для получения уравнений движения вязкой жидкости при малых числах Рейнольдса будем исходить из общей системы уравнений Навье — Стокса

div v = 0. (1)

Рассмотрим внешнюю задачу. Пусть характерный раз­мер обтекаемого тела а, а скорость на бесконечности . Введем безразмерные независимые переменные и безразмер­ные искомые функции

, ,,,,. (2)

После перехода к новым независимым переменным и новым ис­комым функциям получим

,

. (3)

При этом искомая функция u удовлетворяет на бесконечности

условию u∞ = Re. Модуль искомой величины u = |u| =по

существу является местным (вычисленным в данном месте) чис­лом Рейнольдса. Предположение о малости чисел Рейнольдса означает, что

,

или ,,. (4)

Поскольку безразмерная скорость и ее компоненты и_х, и_у, и_z меняются на величины порядка их самих на расстояниях по­рядка единицы (характерного размера), то в этих течениях на­ряду с (4) имеем

. (5)

Из (4) и(5) следует, что произведения вида

являются величинами второго порядка малости. Пренебрегая в уравнении (3) величинами второго порядка малости по срав­нению с величинами первого порядка малости, получим уравне­ния

,

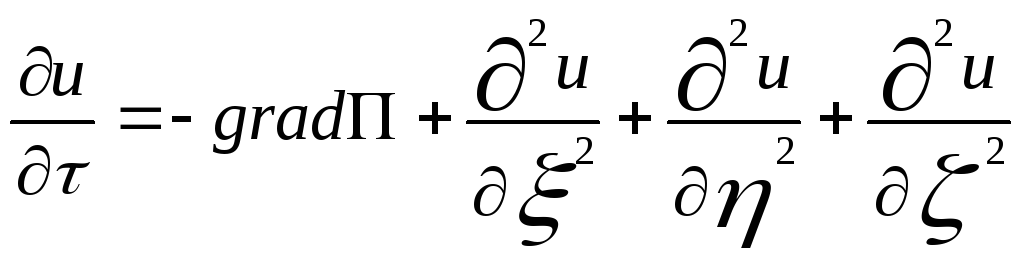. (6)

Уравнения (6) есть уравнения движения вязкой жидкости при малых числах Re, записанные в безразмерном виде. Если теперь в уравнениях (6) снова вернуться к размерным величинам, то будем иметь систему

,

. (7)

Уравнения (7)—уравнения Стокса для движения вязкой жид­кости при малых числах Re. Иногда их называют уравнениями Стокса для медленных движений. В случае установившихся дви­жений они имеют вид

,

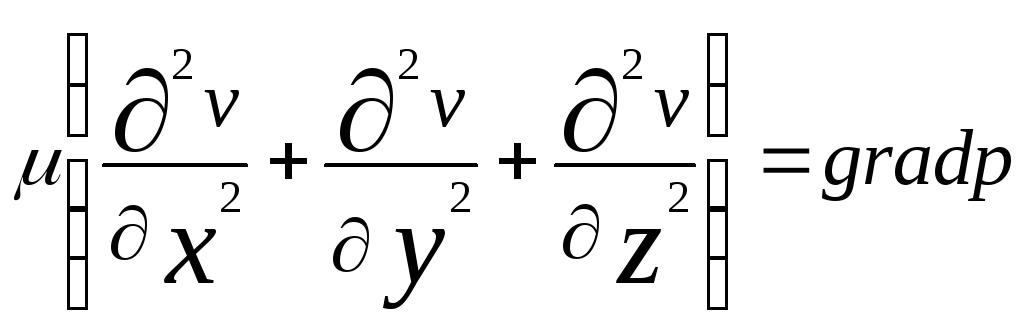. (8)

Системы (7), (8) отличаются от исходных уравнений (1), в частности, тем, что они линейны, поэтому строить их решение гораздо проще.