Способы вычисления определенного интеграла Интегрирование по частям

Пусть и- дифференцируемая функция от. Тогда

(8.21)

Проинтегруем тождество (8.21) в границах от до, получим

(8.22)

Поскольку , тои равенство (8.22) приобретает вид

или окончательно (8.23)

Формула (8.23) и выражает способ интегрирования по частям определенного интеграла. Видно, что она подобна формуле (7.12) интегрирования по частям неопределенного интеграла.

Пример.1. Вычислить .

Решение

Пример 2. Вычислить .

Решение.

Интегрирование подстановкой

Пусть надо вычислить определенный интеграл

где - непрерывная нафункция, а первообразной для нее нет в таблице простейших интегралов. Тогда произведем замену переменной, а именно, введем новую переменнуютаким образом:, где- непрерывно дифференцируема нафункция.

Если при этом будут выполняться такие условия:

1. при изменении отдопеременная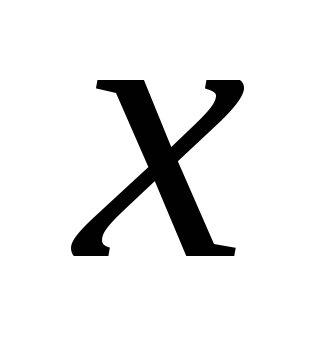изменяется отдо, то есть

. (8.24)

2. сложная функция определена и непрерывна на отрезке, то справедлива такая формула

(8.25)

Формула (8.25) и выражает собою суть метода подстановки.

Замечание. При вычислении определенного интеграла с помощью замены переменной нет необходимости возвращаться к старой переменной (как это нужно было делать при вычислении неопределенного интеграла) достаточно лишь учесть границы интегрирования соответственно (8.24).

Пример 8.3. Вычислить

Решение

Введем новую переменную . Тогда

. Вычислим границы интегрирования и результат представим в виде табл. 1. Таблица 1

x	0	3
t	1	2

из которой видно, что при , а при. Итак, после введении новой переменной получим

Пример 4.Вычислить.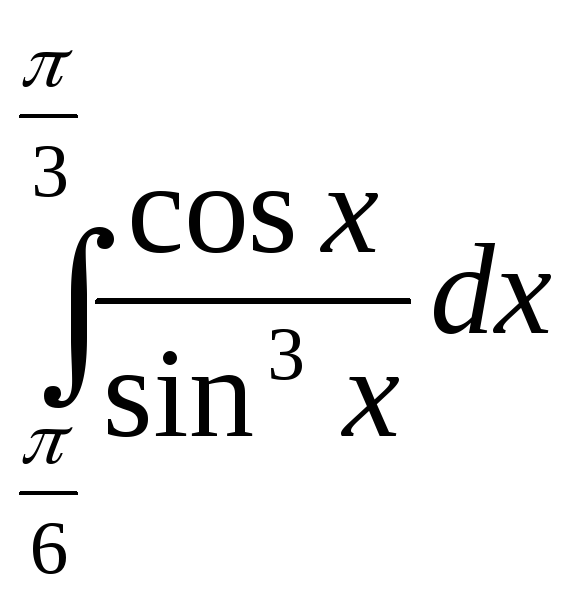

Решение.

Произведем замену переменной: . Тогда, а границы интегрирования приобретают значения: при

при

Итак, получаем

Таким образом, видим, что различие в применении метода замены переменной в неопределенном и определенном интеграле состоит в том, что в втором случае не надо возвращаться к старой переменной, поскольку при замене переменной изменяются также и границы интегрирования.

Приближенное вычисление определенного интеграла

Пусть надо вычислить , но первообразная для функциине выражается через элементарные функции. Тогда применить формулу Ньютона-Лейбница невозможно. В таких случаях применяются методы приближенного вычисления определенных интегралов. Рассмотрим их, используя определение интеграла как границы интегральной суммы. Разделим отрезокточкаминачастичных отрезков равной длины. Обозначим длину каждый из них через. Тогда

Обозначим через значения функциив точках, то есть

.

Составим суммы:

,

.

Каждая из этих сумм представляет собой интегральную сумму для на отрезкеи поэтому приближенно выражает интеграл

, (8.26)

. (8.27)

Из рис. 8.7 видно, что формула (8.26) выражает площадь ступенчатой фигуры, составленной из прямоугольников, вписанных в криволинейную трапецию, а формула (8.27) выражает площадь ступенчатой фигуры, составленной из прямоугольников, описанных вокруг криволинейной трапеции. Поэтому формулы (8.26; 8.27) называются формулами прямоугольников. Погрешность при вычислении интегралов за формулами прямоугольников будет тем меньше, чем больше число n. Она выражается формулой

где-максимальное значение абсолютной величиныпроизводнойна.

Более точное значение определенного интеграла получим, если данную кривую заменим не ступенчатой линией, как это делается в формуле прямоугольников, а вписанной ломаной (рис. 8.8).

Тогда площадь криволинейной трапеции заменится суммой площадей прямолинейных трапеций, ограниченных сверху хордами

Поскольку площадь первой из этих трапеций равна , площадь второй равняется, то

или

. (8.28)

Легко видеть, что она дает среднее арифметическое из формул (8.26 и 8.27). Формула (8.28) называется формулой трапеций. В этом случае погрешность вычисляется по формуле

где - минимальное значение абсолютной величины второй производнойна.

Более точные результаты можно получить по формуле Симпсона (или формуле парабол), которая имеет вид:

(8.29)

При этому надо обратить внимание на то, что число частичных отрезков, на которые разбивается отрезок, должно быть обязательно четным, то есть. Тогда каждые две соседних криволинейных трапеции, на которые разбилась вся криволинейная трапеция(рис. 8.8), заменяютсяпараболической трапецией, площадь которой исчисляется по формуле ,

гдеи- крайние ординаты,- ордината кривой в середине отрезка, а- расстояние между ординатамии(рис. 8.9).

Погрешность при этом может быть вычислена по формуле

где - максимальное значение абсолютной величины производнойна отрезке.

Пример.5. Вычислить приближенно.

Точное значение его . З точностью до седьмого знака. Вычислим теперь его значение, пользуясь формулами (8.26-8.29). Для этого разделим отрезокна 10 равных отрезков. Тогда длина каждого из них будет.

Составим табл. 2 значений подынтегральной функции в точках разбиения .

Таблица 2

Тогда по формуле (8.26) получим.

По формуле (8.27) .

По формуле (8.28) .

По формуле Симпсона (8.29)

Таким образом, по формуле Симпсона при получили 5 верных знаков, по формуле трапеций - лишь три верных знака, за формулами прямоугольников мы можем быть уверены только в одном знаке.