6) Логарифмическая функция, е свойства и график

Функцию, заданную формулой y=logax, называют логарифмической функцией с основанием a.

(a>0,a≠1)

 

 

Основные свойства логарифмической функции:

1. Область определения логарифмической функции - множество всех положительных чисел.

D(f)=(0;+∞);

 

2. Множество значений логарифмической функции - множество R всех действительных чисел.

E(f)=(−∞;+∞);

 

3. Логарифмическая функция на всей области определения возрастает при a>1 или убывает

 при 0<a<1.

 

Обрати внимание!

 Логарифмическая функция не является ни четной, ни нечетной;  не имеет ни наибольшего, ни наименьшего значений;  не ограничена сверху, не ограничена снизу;       

График любой логарифмической функции y=logax проходит через точку (1;0).

Построим графики двух функций

 

Пример:

1. y=log2x, основание 2>1

x	14	12	1	2	4	8
y=log2x	−2	−1	0	1	2	3

 

 

Пример:

2. y=log13x основание 0<13<1

x	9	3	1	13	19
y=log13x	−2	−1	0	1	2

 

 

Логарифмическая функция y=logax и показательная функция y=ax, где (a>0,a≠1), взаимно обратны.

 

           

7) Основные тригонометрические тождества.

Равенство, состоящее из тригонометрических соотношений, справедливое для всех значений входящих в него величин углов, называется тригонометрическим тождеством.

Рассмотрим наиболее важные из тригонометрических тождеств.

Основные тригонометрические соотношения связаны тождествами:

1) tg a = sin a /cos a  2) sin^2 a + cos^2 a = 1 3) 1 + tg^2 a = 1/cos^2 a  4) 1 + 1/tg^2 a = 1/sin^2 a  5) sin(90^o– a ) = cos a  6) cos(90^o– a ) = sin a

Рассмотрим прямоугольный треугольник с острым углом a при вершине А .

Докажем основные тригонометрические тождества.

Воспользуемся теоремой Пифагора.

Если мы разделим обе части равенства на квадрат длины стороны АВ и вспомним определения косинуса и синуса угла, получим второе тождество.

При доказательстве третьего и четвертого утверждений, воспользуемся предыдущим доказательством.

Докажем третье утверждение теоремы. Воспользуемся только что полученным равенством. Разделим обе его части на cos² a и получим требуемое тождество.

Докажем четвертое утверждение теоремы. Опять воспользуемся вторым тождество. Разделив обе части на sin² a , получим четвертое тождество.

Докажем пятое и шестое утверждения теоремы, предварительно повторив по Cправочнику теорему о сумме углов треугольника.

Выразим величину угла при вершине В через угол a . Вспомнив определения синуса и косинуса для углов при вершинах А и В, получаем пятое утверждение теоремы.

И наконец докажем шестое утверждения теоремы. Опять воспользуемся определениями синуса и косинуса для углов при вершинах А и В, чтобы получить последнее утверждение теоремы.

Еще раз посмотри на доказанные формулы и запомни их!

8)Общие формулы корней уравнения tg x=a, cos X=a

Простейшие тригонометрические уравнения.

1. sinx = a, |a|1

x = (–1 ) ^k arcsin a +  k , k 

Частные случаи:

a = –1	a = 0	a = 1
sinx = –1	sin x = 0	sin x =
x = – + 2 k , k	x =  k , k	x = + 2 k , k
	| a| >1 корней нет

2. cos x = a , |a|1

x = ± arccos a + 2 k , k 

Частные случаи:

a = –1	a = 0	a = 1
cos x = –1	cos x = 0	cos x = 1
x = + 2 k , k	x =+ k , k	x = 2 k , k
	|a| >1 корней нет

3. tg x = a , a 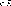 x = ± arctg a +  k , k 

Основные типы тригонометрических уравнений.

• Уравнения, сводящиеся к простейшим.

• Уравнения, сводящиеся к квадратным.

• Однородные уравнения: asinx + bcosx = 0,    a sin ² x + b sinxcosx + c cos ² x = 0.

• Уравнения вида a sinx + b cosx = с , с ≠ 0.

• Уравнения, решаемые разложением на множители.

• Нестандартные уравнения.

9) Общие формулы корней уравнения tg X=a, ctg X=a

Уравнение tgx=a

Уравнение tgx=a имеет решения x=arctga+πk,k∈Z

Что же такое arctga?

Арктангенс  в переводе с латинского означает дуга и тангенс. Это обратная функция.

arctga (арктангенс a) - это такое число из отрезка (−π2;π2), тангенс которого равен a.

 

Говоря иначе:

arctga=x⇒tgx=a,x∈(−π2;π2)

Теорема. arctg(−a)=−arctga.

Уравнение ctgx=a

Уравнение ctgx=a имеет решения x=arcctga+πk,k∈Z

Что же такое arcctga?

arcctga (арккотангенс a) - это такое число из отрезка (0;π), котангенс которого равен a.

 

Говоря иначе:

arcctga=x⇒ctgx=a,x∈(0;π)

 

Теорема. arcctg(−a)=π−arcctga

10) Функция y=sin x, ее свойства и график

Функция y=sinx определена на всей числовой прямой, является нечётной и периодической с периодом 2π.  

График этой функции можно построить таким же способом, как и график функции y=cosx, начиная с построения, например,  на отрезке [0;π]. 

Однако проще применить формулу sinx=cos(x−π2), которая показывает, что график функции y=sinx можно получить сдвигом графика функции  y=cosx вдоль оси абсцисс вправо на π2 

 

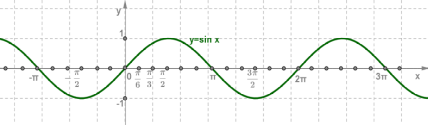
График функции y=sinx

Кривая, являющаяся графиком функции y=sinx, называется синусоидой.

Свойства функции y=sinx

1. Область определения - множество R всех действительных чисел.

2. Множество значений - отрезок [−1;1]

3. Функция y=sinx периодическая с периодом T=2π 

4. Функция y=sinx- нечётная.

5. Функция y=sinx принимает: - значение, равное 0, при  x=πn,n∈Z  - наибольшее значение, равное 1, при x=π2+2πn,n∈Z  - наименьшее значение, равное −1, при x=−π2+2πn,n∈Z   - положительные значения на интервале (0;π) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z

- отрицательные значения на интервале (π;2π) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z

6. Функция y=sinx

- возрастает на отрезке

 [−π2;π2] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z - убывает на отрезке

 [π2;3π2] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z

 

11) Функция y=cos x, ее свойства и график

 а)  Область определения:   D (cos x) = R .

    б)  Множество значений:   E (cos x ) = [ – 1 ,  1 ] . в)  Четность, нечетность:   функция четная.

    г)  Периодичность:   функция периодическая с основным периодом  T = 2.

    д)  Нули функции:  cos x = 0  при   x = +n,   n Z.

   е)  Промежутки знакопостоянства:

;   .

.      ж)  Промежутки монотонности:

;

.

      з)  Экстремумы:

;            .

     График функции    y= cos x   изображен на рисунке.

12) Функция y=tg x, ее свойства и график.

Функция y=tgx определена при x≠π2+πn,n∈Z, является нечётной и периодической с периодом π.

Поэтому достаточно построить её график на промежутке [0;π2)

Выберем для построения контрольные точки, через которые проведём плавную кривую на координатной плоскости.

 tg0=0tgπ6=3√3tgπ4=1tgπ3=3√

 

Затем, отобразив её симметрично относительно начала координат, получим график на интервале (−π2;π2) 

Используя периодичность, строим график функции y=tgx на всей области определения.  

График функции y=tgx называют тангенсоидой.  

Главной ветвью графика функции y=tgx обычно называют ветвь, заключённую в полосе (−π2;π2)

Свойства функции y=tgx

1. Область определения - множество всех действительных чисел x≠π2+πn,n∈Z

 

2. Множество значений - множество R всех действительных чисел

 

3. Функция y=tgx периодическая с периодом π

 

4. Функция y=tgx нечётная

 

5. Функция y=tgx принимает:

- значение 0, при x=πn,n∈Z;

- положительные значения на интервалах (πn;π2+πn),n∈Z;

- отрицательные значения на интервалах (−π2+πn;πn),n∈Z.

 

• Функция y=tgx возрастает на интервалах (−π2+πn;π2+πn),n∈Z. 

13) Функция y=ctgx и её свойства и график

Функция y=ctgx определена при x≠πn,n∈Z, является нечётной и периодической с периодом π.

Рассуждая аналогично как при построении графика функции y=tgx, можно построить график функции y=ctgx.

График функции y=ctgx, как и  график функции y=tgx, называют тангенсоидой.  

 

Главной ветвью графика функции y=ctgx обычно называют ветвь, заключённую в полосе от x=0 до x=π.

 

Свойства функции y=ctgx

1. Область определения - множество всех действительных чисел x≠πn,n∈Z

 

2. Множество значений - множество R всех действительных чисел

 

3. Функция y=ctgx периодическая с периодом π

 

4. Функция y=ctgx нечётная

 

5. Функция y=ctgx принимает:

- значение 0, при x=π2+πn,n∈Z;

- положительные значения на интервалах (πn;π2+πn),n∈Z;

- отрицательные значения на интервалах (−π2+πn;πn),n∈Z.

 

6. Функция y=ctgx убывает на интервалах (πn;π+πn),n∈Z.