
- •Brief Contents
- •Contents
- •Preface
- •Who Should Use this Book
- •Philosophy
- •A Short Word on Experiments
- •Acknowledgments
- •Rational Choice Theory and Rational Modeling
- •Rationality and Demand Curves
- •Bounded Rationality and Model Types
- •References
- •Rational Choice with Fixed and Marginal Costs
- •Fixed versus Sunk Costs
- •The Sunk Cost Fallacy
- •Theory and Reactions to Sunk Cost
- •History and Notes
- •Rational Explanations for the Sunk Cost Fallacy
- •Transaction Utility and Flat-Rate Bias
- •Procedural Explanations for Flat-Rate Bias
- •Rational Explanations for Flat-Rate Bias
- •History and Notes
- •Theory and Reference-Dependent Preferences
- •Rational Choice with Income from Varying Sources
- •The Theory of Mental Accounting
- •Budgeting and Consumption Bundles
- •Accounts, Integrating, or Segregating
- •Payment Decoupling, Prepurchase, and Credit Card Purchases
- •Investments and Opening and Closing Accounts
- •Reference Points and Indifference Curves
- •Rational Choice, Temptation and Gifts versus Cash
- •Budgets, Accounts, Temptation, and Gifts
- •Rational Choice over Time
- •References
- •Rational Choice and Default Options
- •Rational Explanations of the Status Quo Bias
- •History and Notes
- •Reference Points, Indifference Curves, and the Consumer Problem
- •An Evolutionary Explanation for Loss Aversion
- •Rational Choice and Getting and Giving Up Goods
- •Loss Aversion and the Endowment Effect
- •Rational Explanations for the Endowment Effect
- •History and Notes
- •Thought Questions
- •Rational Bidding in Auctions
- •Procedural Explanations for Overbidding
- •Levels of Rationality
- •Bidding Heuristics and Transparency
- •Rational Bidding under Dutch and First-Price Auctions
- •History and Notes
- •Rational Prices in English, Dutch, and First-Price Auctions
- •Auction with Uncertainty
- •Rational Bidding under Uncertainty
- •History and Notes
- •References
- •Multiple Rational Choice with Certainty and Uncertainty
- •The Portfolio Problem
- •Narrow versus Broad Bracketing
- •Bracketing the Portfolio Problem
- •More than the Sum of Its Parts
- •The Utility Function and Risk Aversion
- •Bracketing and Variety
- •Rational Bracketing for Variety
- •Changing Preferences, Adding Up, and Choice Bracketing
- •Addiction and Melioration
- •Narrow Bracketing and Motivation
- •Behavioral Bracketing
- •History and Notes
- •Rational Explanations for Bracketing Behavior
- •Statistical Inference and Information
- •Calibration Exercises
- •Representativeness
- •Conjunction Bias
- •The Law of Small Numbers
- •Conservatism versus Representativeness
- •Availability Heuristic
- •Bias, Bigotry, and Availability
- •History and Notes
- •References
- •Rational Information Search
- •Risk Aversion and Production
- •Self-Serving Bias
- •Is Bad Information Bad?
- •History and Notes
- •Thought Questions
- •Rational Decision under Risk
- •Independence and Rational Decision under Risk
- •Allowing Violations of Independence
- •The Shape of Indifference Curves
- •Evidence on the Shape of Probability Weights
- •Probability Weights without Preferences for the Inferior
- •History and Notes
- •Thought Questions
- •Risk Aversion, Risk Loving, and Loss Aversion
- •Prospect Theory
- •Prospect Theory and Indifference Curves
- •Does Prospect Theory Solve the Whole Problem?
- •Prospect Theory and Risk Aversion in Small Gambles
- •History and Notes
- •References
- •The Standard Models of Intertemporal Choice
- •Making Decisions for Our Future Self
- •Projection Bias and Addiction
- •The Role of Emotions and Visceral Factors in Choice
- •Modeling the Hot–Cold Empathy Gap
- •Hindsight Bias and the Curse of Knowledge
- •History and Notes
- •Thought Questions
- •The Fully Additive Model
- •Discounting in Continuous Time
- •Why Would Discounting Be Stable?
- •Naïve Hyperbolic Discounting
- •Naïve Quasi-Hyperbolic Discounting
- •The Common Difference Effect
- •The Absolute Magnitude Effect
- •History and Notes
- •References
- •Rationality and the Possibility of Committing
- •Commitment under Time Inconsistency
- •Choosing When to Do It
- •Of Sophisticates and Naïfs
- •Uncommitting
- •History and Notes
- •Thought Questions
- •Rationality and Altruism
- •Public Goods Provision and Altruistic Behavior
- •History and Notes
- •Thought Questions
- •Inequity Aversion
- •Holding Firms Accountable in a Competitive Marketplace
- •Fairness
- •Kindness Functions
- •Psychological Games
- •History and Notes
- •References
- •Of Trust and Trustworthiness
- •Trust in the Marketplace
- •Trust and Distrust
- •Reciprocity
- •History and Notes
- •References
- •Glossary
- •Index

The Winner’s Curse |
5 |
and Auction Behavior |
Consider Rick, who found a rare coin listed on an online auction website. The auction is to last two weeks. Rick is very familiar with coin collecting and has a very good idea of the coin’s value. He places a bid based upon the value he believes the coin holds when he discovers the auction, and is satisfied because his bid is the highest thus far. He then waits, checking the auction site daily to see if his bid is still the top. One day before the auction is to close, he notices that someone has outbid him by at least $10. Rick quickly responds by upping his bid by $20, only to discover that he is still being outbid. Thus he follows up with another increase of $30, obtaining the top bid and winning the coin. Rick is very satisfied to have won the auction, and he doesn’t seem to be bothered by paying almost $50 more for the coin than he thought it was worth.
With the advent of online auctions, personal experience with bidding and auction behavior is much more prevalent than it once was. Most who have participated in online auctions can attest to a certain level of gaming and scheming by auction participants. Students have suggested what they consider to be optimal strategies. For example, one suggests not to bid until the very end of the auction so that it is difficult for your competitors to react to your bid and thereby win the object of the auction. In almost all cases, the strategies suggested the importance of tricking or taking other bidders by surprise with your own actions or strategy. How should one best respond to the actions of others in an auction? What sorts of psychological biases govern individual behavior in an auction setting? This chapter describes the regular behaviors found in auctions and their implications for strategy, marketing, and procurement. When the behavior of one person can affect the outcomes of others and vice versa, we say that the people are engaged in a game. Economists generally use a game-theory model to predict or describe behavior in games. This chapter builds on the basic elements of game theory, incorporating behavioral heuristics to describe deviations from the predictions of game-theory approaches.
Rational Bidding in Auctions
The most common type of auction found online is a second-price auction. A secondprice auction awards the object of the auction to the highest bidder, with the price being determined by the second-highest bid. An auction with n participants can be described as a game among n players. Each player might value the object of the
93

|
|
|
|
|
94 |
|
THE WINNER’S CURSE AND AUCTION BEHAVIOR |
auction differently. Let vi represent the monetary value of the auction object to player i. Each participant’s behavior must depend on the payoffs that he or she will receive for each possible strategy. More formally, a game is a collection of available actions for all players and a set of payoffs, with one payoff value corresponding to each possible collection of actions by all players. Thus to specify a game, we must list the players, the actions available to each player, and the payoffs for every result. First, let’s examine the case of a second-price sealed-bid auction, often referred to as a Vickrey auction. A sealed-bid auction means that no bidder is aware of other bidders’ bids at the time they place their own bid. Because players cannot observe the bids of others, a player cannot condition his actions on the actions of other players. In this case, bidder i’s payoffs can be characterized as
πi = vi − p if |
xi > p |
5 1 |
0 if |
xi ≤ p, |
|
where p is the second-highest bid and thus the realized price for the object, and xi is bidder i’s bid. First, consider a bid with xi < vi. In this case, if the bidder wins the auction, xi > p, then the bidder obtains the value from the good but loses the auction price, resulting in a net gain of vi − p > 0. Because this value is positive, the bidder could only benefit from wining the auction in this case.
Alternatively, suppose the bidder lost the auction, xi < p. In this case, the bidder obtains zero benefit. If the price is above his bid, but below his valuation, vi > p > xi, then increasing his bid to any value above p will result in winning the item and obtaining vi − p > 0, which is strictly better than if he had bid below p. Thus, the bidder might fail to purchase the item when it is in his best interest to obtain it if he bid below his valuation and the realized price is also below his valuation of the object.
Suppose instead that the bidder bid above his value, xi > vi. If his bid is above the price, then he wins the item, obtaining a value of vi − p. This is positive if vi > p, but nonpositive otherwise. Thus, if the price realized is over the bidder’s value but below his bid, xi > p > vi, the bidder is strictly worse off than if he had bid below p. Thus, if the bidder bids above his valuation of the object, any realized price above his valuation could result in his obtaining the item at more than it is worth, resulting in a loss.
Finally, suppose the bidder bids exactly his valuation, xi = vi. In this case, if the realized price is below his bid, he will obtain vi − p > 0, which is the most he could receive under any possible bid. Alternatively, if the realized price is above his bid, then he obtains 0. Increasing his bid could obtain the item, but it would necessarily result in a loss because he would pay more than it was worth to him. Thus, in this case, 0 is the best outcome that could be obtained under any bid. Bidding one’s value results in obtaining the highest payout of any strategy, no matter what price results from the combination of all participants’ bids. When a strategy produces the highest payout to the individual of any possible strategy under all possible outcomes, the strategy is called a dominant strategy. In this case, each player in the Vickrey auction has a dominant strategy to bid his or her valuation of the object no matter what anyone else does. Thus a rational model would predict that people bid their valuation no matter what. In this scenario, the bidder

|
|
|
|
Rational Bidding in Auctions |
|
95 |
|
who values the good the most wins the auction and pays the second-highest valuation for the item.
Suppose instead that people could observe others’ bids and could sequentially increase their bid if they decided. In this case, whenever all other bids were below the bidder’s valuation, the bidder should bid above all others. If he subsequently saw further bids from others above his previous bid but below his valuation, he should increase his bid again. However, if any bid occurs above his value, he should cease to bid. This will lead to an outcome where the bidder who values the good the most will eventually outbid all others and will pay the second-highest bid, which will be given by the second-highest valuation, just as in the sealed-bid auction. Thus, there is no advantage to gaming a second-price auction. One could just as easily bid one’s valuation of the item at the onset of the auction and wait to see if others valued the item more or less.
Finally, consider a first-price auction. A first-price auction is an auction mechanism where the top bidder wins the item but must pay his own bid for the item. In this case, the winner’s payout can be described as
πi = v − xi |
if |
xi = p |
5 2 |
0 |
if |
xi < p, |
|
so that the winner obtains the value of the item, minus his bid if his bid is the realized price, and obtains zero if his bid is less than the realized price. If this were a first-price open-bid auction, then the bidder could observe the bids of others. If there were any bids above his valuation, he would choose to bid at a lower value, lose the item, and gain zero. Alternatively, if the highest bid by any other player were below his valuation, he would choose to bid just slightly higher than the next highest bid, so as to obtain the item, gaining the difference between his valuation and his bid—essentially the next-highest bid. Thus, the first-price open-bid auction results in outcomes that are much like the second-price auction. Everyone should bid up to their assessed value except the bidder with this highest valuation, who bids as high as the second-highest value and obtains the item. Thus, in a wide range of auction types, the bidder valuing the object the most should win and should pay an amount equal to the second-highest valuation.
In more-general sets of games it is not always possible to find a dominant strategy. The primary tool to make predictions when the player’s outcome depends on the actions of others is the concept of the Nash equilibrium. To define the Nash equilibrium, we need first to define a few useful terms.
Define a node as any point in the game where a decision can be made by player i and the information available to the player at that point. For example, in playing a game of tic-tac-toe, the beginning of the game places player 1 at a node where she can choose to place her mark in any of nine squares, with no knowledge of where player 2 will choose to respond. If player 1 places her mark in the center square, this places player 2 at a node where player 1 has placed a mark in the center square; he now knows where player 1 placed her mark and can choose to place his mark on any of the remaining eight squares. Had player 1 placed her mark in the upper left square, we would have arrived at a

|
|
|
|
|
|
96 |
|
THE WINNER’S CURSE AND AUCTION BEHAVIOR |
|
|
|
different node where eight squares were available, but now the upper left square is taken, |
||
|
|
and the center square is available. |
|
|
|
|
|
A strategy is a collection of the decisions a player intends to make at each possible |
|
|
|
node of the game should that node be reached. It is important to differentiate between a |
||
|
|
strategy and an action. One action might be “place an X on the center square.” A strategy |
||
|
|
would be a long list of actions, one for each node, such as “if player 1’s first move is to |
||
|
|
place an O in the top left corner, then my first move will be to place an X in the center |
||
|
|
square; if player 1’s first move is to place an O in the upper middle square, then my first |
||
|
|
move . . . ,” and so on, describing every action in response to every action or history of |
||
|
|
actions in the game. Let πi si S − i be the payoff received by player i for playing strategy |
||
|
|
si, when all other players are playing strategies represented by the symbol S − i. |
||
|
|
|
The Nash equilibrium is a collection of strategies S = s1, |
, sn , such that for each |
player i, πi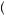 si
si S − i
S − i ≥ πi
≥ πi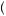 si
si S− i
S− i , where S = si
, where S = si 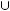 S− i. Intuitively, the Nash equilibrium is a set of strategies, one for each player, such that each player is maximizing his or her payoff given the strategies of all others involved. Thus, given the strategies of all others, any single player should not be better off for choosing a different strategy. In the secondprice auction, a Nash equilibrium is given by each bidder bidding his or her valuation. In the open-bid first-price auction, a Nash equilibrium is given by each bidder choosing to bid his own valuation unless he is the top bidder, in which case he bids just above the second-highest bidder. In general, if any player has a dominant strategy, all Nash equilibriums must require this player to play his dominant strategy. The Nash equilibrium is widely considered the basic requirement for rationality in a game.
S− i. Intuitively, the Nash equilibrium is a set of strategies, one for each player, such that each player is maximizing his or her payoff given the strategies of all others involved. Thus, given the strategies of all others, any single player should not be better off for choosing a different strategy. In the secondprice auction, a Nash equilibrium is given by each bidder bidding his or her valuation. In the open-bid first-price auction, a Nash equilibrium is given by each bidder choosing to bid his own valuation unless he is the top bidder, in which case he bids just above the second-highest bidder. In general, if any player has a dominant strategy, all Nash equilibriums must require this player to play his dominant strategy. The Nash equilibrium is widely considered the basic requirement for rationality in a game.
EXAMPLE 5.1 Second-Price Auctions
John Kagel, Ronald Harstad, and Dan Levin conducted a set of experiments to test the predicted Nash equilibrium under several types of auctions. Among these, they tested the Vickrey auction mechanism. Participants were randomly assigned a private valuation for winning the auction—in other words, each was assigned a value they would receive if they won the auction and each participant’s value was different. This valuation took the form of an amount of money they would receive if they happened to win the auction. Participants were informed of the auction mechanism and they engaged in several rounds of Vickrey auctions. In each round, the participant was assigned a new private valuation for winning. The Nash equilibrium strategy is to bid one’s private value for the auction, but the bids were, on average, substantially above the private valuation assigned. On average, the bids were between 12 percent and 20 percent above the private value, with larger percentages when the private value was lower. Participants experienced dozens of Vickrey auctions, with no evidence that their bids were converging to the dominant strategy of bidding one’s valuation. This led to the curious condition that in 80 percent of the auctions, the price (determined by the second-highest bidder) was above the second-highest valuation in the auction, with 36 percent of the auction winners paying a price that was above their own private valuation. These 36 percent were winners only in the nominal sense of the word, as they were the only participants in these auctions to lose money.
