5. Сравнительный анализ эффективности методов решения задач одномерной нелинейной оптимизации без ограничений. Стратегии выбора исходного интервала неопределенности и поиска глобального экстремума.

N – кол-во вычислений целевой ф-ии f(x)

– конечный интервал неопределенности

, где– точность

I) Алгоритмы пассивного поиска

1. Алгоритм равномерного поиска

II) Алгоритмы активного поиска

2. Алгоритм равномерного блочного поиска

;n- число точек в блоке,m- число итераций

3. Деление интервала пополам

4. Метод дихотомии

5. Метод золотого сечения

6. Метод чисел Фибоначчи

по эфф-ти примерно одинаков с методом золотого сечения

III) Методы основанные на аппроксимации функции

7.метод парабол

Невозможно получить выражение для

В общем случае можно говорить, что он достаточно эффективен

Стратегии выбораисходного интервала неопределенности и поиска глобального экстремума.

Исх. данные: поиска

1. k=0;, если, то переход к шагу 2,

иначе h= -h;

Если , то переход к шагу 2, иначе,

2.

2.1.

Если , то

2.2.

Если , то переход к шагу 2.1,k=k+1, иначе, переход к шагу 3.

3.

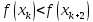Анализ точек . Если, то

иначе , останов

6. Постановка задачи многомерной безусловной оптимизации и классификация методов ее решения. Прямые методы поиска: Гаусса, конфигураций, вращающихся координат, деформируемого многогранника.

Постановка задачи

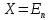,, задана функция. Необходимо найтиmin(илиmax)

исходные данные:

Классификация методов:

1) Прямые методы поиска

Знание целевой ф-ии не нужно, необходимо только уметь вычислять ее в точках

2) Методы первого порядка (градиентные методы)

Нужно знать вид функции, уметь вычислять первую производную. Выбор направления основан на вычислении градиента

3) Методы второго порядка

Нужно знать вид функции, уметь вычислять градиент и матрицу Гесса

Особенности прямых методов:

1)нет необходимости знать вид ф-ии

2)не требуется регулярность и непрерывность

3)не требуется вычисление производной первого порядка

Метод Гаусса

На каждом этапе осуществляем движение по осям координат. Двигаемся по напр. находимmin. Из новой точки идем вдоль другой оси координат и т.д.

Критерии остановки: а)

б)

1. задаем . k=0–номер итерации

2.

…………………………………………………………….

3.если, то; f()=f()

Иначе k=k+1, перейти к шагу 2.

Недостатки метода:

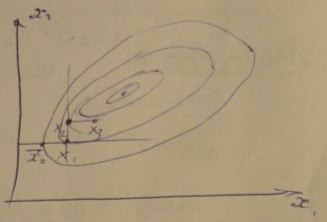
1) Если линии равного уровня вытянуты (ф-ии овражного типа), то сходимость данного метода будет очень плохой.

2) Если вид такой, то алгоритм даст неправильную точку

Метод конфигураций

Метод состоит из 2-х этапов:

1) исследовательский поиск (поиск направления)

2) поиск по образцу (по определенному направлению)

1. задаем x⁰,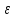,h, иk=0.

2. Введем точку zдля сравнения новой и предыдущей точки,=.j=1

2.1. , еслиf()f(), тои переход к шагу2.3

иначе к шагу2.2

2.2. , еслиf()f(), то, иначе к шагу2.3

2.3. j=j+1 Еслиj<n, то к шагу2.1 иначе к шагу3

3.если =, тоh=h/2, проверяем останов, т.е. если, тои останов, иначе переходим к шагу2

Иначе если , то переход к шагу 4(поиск по образцу).

4. Направление поиска

,

k=k+1 переход к шагу 2.

Метод вращающихся координат

Шаг 1. иk= 0.

Шаг 2. ;

;

…………………………

;

Шаг 3. Если , тои остановка

Иначе к шагу4.

Шаг 4. Используя процедуру Грамма – Шмидта находим

k=k+1, переходим к шагу2

Процедура Грамма-Шмидта

(над всем кроме поставить вектора)

Пусть –полученная С.К. на шагеk

– новая С.К.

Введем систему вспомогательных векторов

……………

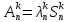
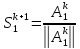
Введем еще вспомогательные вектора

- вектор ортогональныйS₁

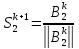
Аналогично

l=2..n

Таким образом получим новую С.К.

Если 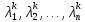=0 => оставляем старые

Метод деформирующего многогранника.

1. Построение исходного многогранника k=0

2.(отражение) выч-м 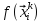i=1..n

– центр тяжести,imax

; α – коэффициент отраженияα>= 1. Обычноα=1.

a)Шаг 3.2

б) Шаг 3.1

a) Шаг 3.2

3.

3.1(растяжение)

; β – коэффициент растяжения, β2 (обычно=2)

Если 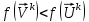, то строим новый симплекс(), переход к шагу 2

Иначе

3.2(сжатие) если условие а)

если условие б);– коэффициент сжатия, обычноj=0,5

Если , то выполняется редукция

переход к шагу 3.3

иначе новый симплекс (замена) и переход к шагу2

3.3 Если , то,f() и остановка

Иначе k=k+1 переход к шагу 2.

7. Сопряженные направления и особенности их использования при решении задач многомерной безусловной оптимизации. Суть методов прямого поиска и градиентных методов, основанных на сопряженных направлениях. Их сравнительный анализ.

–система направлений.

Эта система будет сопряженной, если

H– некоторая положительно определенная квадратичная матрица

Теорема 1:Если задана система сопр. направлений и целевая функция квадратична, то поиск экстремума требует n шагов, при этом порядок использования направлений значения не имеет.

Теорема 2Для матрицыHсуществует хотя бы одна система сопряженных направлений, и в качестве этой системы могут выступать собственные вектора.

Метод сопряженного градиента.

Задано x^o=> первое направление

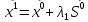
;- выбирается так, чтои– сопряженные

;

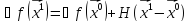
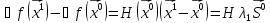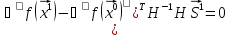
– т.к. они перпендикуляры

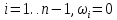
Алгоритм:

1.Задаем,k= 0.

2.

,

3. j=1

3.1

3.2 Если , тоj=j+1 и переход к шагу 3.1

Иначе – переход к шагу 4.

4.Если , то

Иначе - ,k=k+1 и переход к шагу 2.

Сравнительный анализ

Особенности методов прямого поиска состоят в следующем:

1. Знание целевой функции не требуется. Достаточно умение вычислять ее значение в нужных точках

2. Не требуется регулярность и непрерывность функции

3. Не требуется вычисления (наличия) производной 1 порядка

А для градиентных методов надо:

1. Знать целевую функцию

2. Уметь вычислять ее 1 производную

3. Вычислять ее градиент

Также стоит отметить, что если целевая функция квадратична, то для рассмотренного градиентного метода, основанного на сопряженных направлениях, определение экстремума осуществляется за nшагов.

8. Постановка задачи многомерной безусловной оптимизации и классификация методов ее решения. Методы первого порядка: наискорейшего спуска, покоординатного спуска, Гаусса-Зейделя. Их сравнительный анализ.

Постановка задачи

,, задана функция. Необходимо найтиmin(илиmax)

исходные данные:

Классификация методов:

1) Прямые методы поиска

Знание целевой ф-ии не нужно, необходимо только уметь вычислять ее в точках

2) Методы первого порядка (градиентные методы)

Нужно знать вид функции, уметь вычислять первую производную. Выбор направления основан на вычислении градиента

3) Методы второго порядка

Нужно знать вид функции, уметь вычислять градиент и матрицу Гесса

Метод наискорейшего спуска.

1. k= 0

2. выч-м , где

3. выч-м

4. если =>-min, иначеk=k+1 и переход к шагу2

Метод покоординатного спуска.

1. k = 0, =

2.

...

3., если, то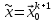и останов, иначе k=k+1 и переход к шагу2

Метод Гаусса-Зейделя

1.

2. Осуществляем циклический поиск по j=1,...,n

3.если , то, иначеk=k+1 и переход к шагу 2.

Сравнительный анализ

Метод наскорейшего спуска:

1) В каждой точке вычисляется градиент функции => много вычислений

2) Плохо ищет экстремум для овражной функции

3) При большой точности поиск может остановиться, не достигнув минимума.

Другие 2 метода уменьшают объем вычислений. Методы покоординатного спуска и Гаусса-Зейделя по сути одинаковы, но в Гаусса-Зейделе меньше вычислений. В покоординатном спуске - более оптимальный поиск. Все 3 метода плохо ищут экстремум овражной функции.