9. Постановка задачи многомерной безусловной оптимизации и классификация методов ее решения. Методы второго порядка: метод Ньютона и его модификации, методы переменной метрики.

Постановка задачи

,, задана функция. Необходимо найтиmin(илиmax)

исходные данные:

Классификация методов:

1) Прямые методы поиска

Знание целевой ф-ии не нужно, необходимо только уметь вычислять ее в точках

2) Методы первого порядка (градиентные методы)

Нужно знать вид функции, уметь вычислять первую производную. Выбор направления основан на вычислении градиента

3) Методы второго порядка

Нужно знать вид функции, уметь вычислять градиент и матрицу Гессе

Метод Ньютона.

1.,k= 0, выч-м–матрица Гессе

2.Вычисляем

3.

4.выч-м

2.Вычисляем

5. Если , то, останов, иначеk=k+1 и переход к шагу 2.

Модификации:

Метод Ньютона-Рафсона(с опт. выбором шага)

, где– минимум ф-ии вдоль направления

Первая модификация метода Ньютона.

Модификация 2 метода Ньютона

Через mитераций вычисляем, т.е. Н не изменяется m итераций, потом вычисляется, потом снова m раз не изменяется и т.д.

10. Задача линейного программирования. Основные определения. Лексикографический вариант прямого симплекс-метода. Вырожденность в задачах линейного программирования. Геометрическая интерпретация симплекс-метода.

Общая форма ЗЛП:

, –целевая ф-ия

–вектор-строка

–вектор-столбец

n–размерность пространства

– ограничения Х

,

кол-во ограничений m

- неотрицательные переменные (остальные- свободные)

– матрица mxn

–вектор-столбец

Основные определения

–столбец

Опр.Любой набор линейно-независимых столбцов (,…,) называется базисом

А=[B,N], где В-матрица, состоящая из линейно-независимых столбцов

N-все остальные.

число базисов

x=,

Опр.Переменные, являющиеся компонентаминазываются базисными переменными

Переменные , не являющиеся компонентаминазываются небазисными переменными

Опр.Решение системыназывается базисным решением.

Каждому базису соответствует базисное решение, но базисное решение может соответсвовать немкольким базисам.

Утв.является базисным решением<=> множество столбцов, которые образуют базис ({}) являются линейно-независимыми.

Опр.Базисным допустимым решением называется любой элемент мн-ва

Утв.является базисно-допустимым решением (бдр) <=> когдаявл. крайней точкой

Опр.Симплекс-таблица называется прямо допустимой, если,i=1..m

Опр.Симплекс-таблица называется двойственно допустимой, если,j=1..n

Утв.Если ЗЛП разрешима, то существует прямо и двойственно допустимая симплекс-таблица

(ЗЛП разрешима, если х не и ф-ия ограничена снизу)

Утв.(достаточное условие оптимальности) если симплекс-таблица явл прямо и двойственно допустимой, то соответствующее базисное решение оптимальное.

Опр.Базисное решение называется вырожденным, если, для которого

Утв.Пусть базисно допустимое решение х невырожденное,,, то тогда существует другое б.д.р., у которого целевая ф-ия меньше

Опр.ЗЛП называется вырожденной, есливырожденное б.д.р.

Утв.В случае невырожденной ЗЛП прямой симплекс-метод является конечным, а если ЗЛП вырожденная, то зацикливание возможно

Лексографический вариант

Опр.Пусть задан вектор=(), тогда векторлексиграфически положительный,если первый отличный от нуля компонент вектора положительный. (0,0,0,1,-1,0…) , т.е. если

Утв.Пусть заданы 2 вектора,, тогда, если.

Если задано множество таких векторов, то среди них всегда можно найти вектор, который будет лексикографическим минимумом : lexmin

Опр.Симплекс-таблица называется нормальной, если все её строки лексографически положительны

Утв.Прямую с.-т. всегда можно преобразовать в нормальную с.-т. путем переобозначения переменных и изменения порядка расположения столбцов

Лексикографический вариант прямого симплекс-метода алгоритма:

0.построить нормальную симплекс-таблицу

1.если с.-т. является двойственно допустимой (т.е. ,j=1..n), то решение оптимальное и конец, иначе переход к шагу2

2.определяем ведущий столбец, т.е. находим такое j=s, что(если их несколько, то выбираем любой из них)

3. если , то конец (ЗЛП решения не имеет), иначе определяем ведущую строкуr:(если 2 одинаковых, то любой)

4.преобразуем симплекс-таблицу с ведущим элементом .(Заменяем соответствующую базисную переменную на небазисную) и переходим к шагу1 (в результате с.-т. остается всегда прямо допустимой)

Утв.Если ЗЛП вырождена, то алгоритм будет конечным (всегда)

Геометрическая интерпретация симплекс-метода.

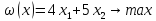
Решение лежит на границе области

25