1. Числовые ряды

1. Понятие числового ряда

Даны члены числовой последовательности u₁, u₂, …, u_n, … . Выражение u₁+u₂+…+u_n+… называется числовым рядом. Числа u₁, u₂, …, u_n, … называются членами ряда. u_n – общий член ряда. Сокращенно ряд записывают .

Запишем суммы S₁ = u­₁, S₂ = u₁+u₂, S₃ = u₁+u₂+u₃, … , S_n = u₁+u₂+…+u_n, … Их называют частными или частичными суммами ряда. Частные суммы образуют бесконечную числовую последовательность S₁, S₂, S₃, …, S_n, … .

Если существует конечный предел последовательности частных сумм , то ряд называютсходящимся. Число S называют суммой ряда и записывают .

Если предел последовательности частных сумм не существует или равен бесконечности, то ряд называется расходящимся.

Пример1.

Задан ряд:

Запишем частную сумму ряда:

Члены ряда представим следующим образом:

Ряд сходится, и его сумма равна 1.

Пример 2.

Ряд называется рядом геометрической прогрессии со знаменателемq. Этот ряд сходится только при |q| < 1 и его сумма равна .

Пример 3.

Ряд называется гармоническим. Он является расходящимся.

1.2. Ряды с положительными членами

Ряд u₁ + u₂ + … + u_n + … называется рядом с положительными членами, если при всех значениях n выполняется неравенство u_n > 0.

Пусть даны два ряда с положительными членами

, (1)

. (2)

Если при всех значениях n выполняется неравенство , то ряд (2) называетсямажорантным по отношению к ряду (1), а ряд (1) называется минорантным (т. е. рядом с меньшими членами).

Теорема (признак сравнения). Из сходимости ряда (2) следует сходимость ряда (1). Из расходимости ряда (1) следует расходимость ряда (2).

Пример 1.

Исследовать сходимость ряда: .

Данный ряд можно сравнить с гармоническим рядом , т. к.. Гармонический ряд расходится, значит, данный ряд расходится.

Пример 2.

Исследовать сходимость ряда: .

Члены данного ряда не больше соответствующих членов ряда

, т. к. . Рядявляется рядом геометрической прогрессии со знаменателем<1. Такой ряд сходится, следовательно, рядсходится.

Пример 3.

Исследовать сходимость ряда: .

Члены данного ряда не меньше соответствующих членов гармонического ряда , т. к.. Гармонический ряд расходится, значит, по признаку сравнения рядов данный ряд расходится.

1.3. Признак Даламбера

Дан ряд с положительными членами u₁ + u₂ + … + u_n + … .

Пусть .

1. Если l < 1, то ряд сходится.

2. Если l > 1, то ряд расходится.

3. Если l = 1, то признак вопроса не решает.

Пример 1.

Исследовать сходимость ряда: ,,.

<1. Ряд сходится.

Пример 2.

Исследовать сходимость ряда: ,,.

. Ряд расходится.

Пример 3.

Исследовать сходимость ряда: ,,.

Ряд сходится.

Пример 4.

Исследовать сходимость ряда: ,,.

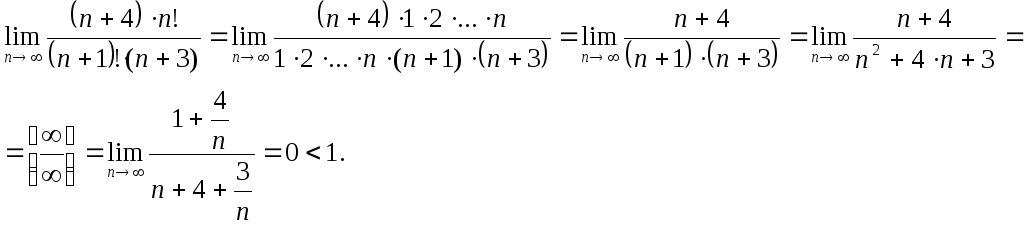
Ряд сходится.

1.4. Интегральный признак Коши сходимости ряда

Дан ряд с положительными членами u₁+u₂+…+u_n+… , члены которого монотонно убывают, т.е. u_n+1 < u_n.

Составим непрерывную невозрастающую положительную функцию f(x), заданную на такую, что приx = 1,2,3,…,n,… значение функции равно соответствующему члену ряда. Функция f(x) называется производящей функцией данного ряда.

Теорема. Если члены данного ряда монотонно убывают (u_n+1 < 0 u_n , n = 1,2, 3, …) и если функция y = f(x) при непрерывна, положительна и монотонно убывает, иf(n)=u_n, тогда

1. если 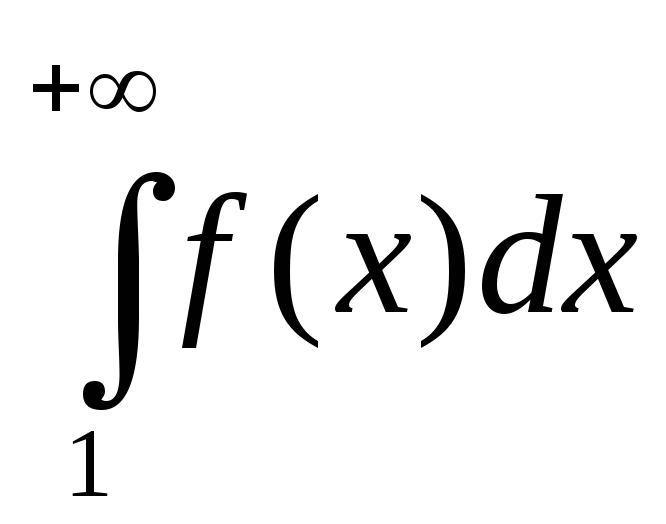сходится, то сходится и данный ряд;

2. если расходится, то расходится и данный ряд.

Пример 1.

Исследовать на сходимость ряд: .

Составим производящую функцию ряда . Вычислим несобственный интеграл этой функции:

.

Несобственный интеграл сходится, сходится и данный ряд.

Пример 2.

Исследовать сходимость числового ряда: .

Составим производящую функцию ряда . Вычислим:

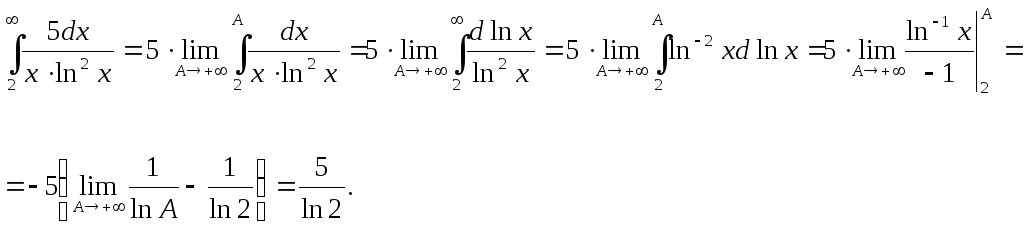
Несобственный интеграл сходится, сходится и данный ряд.

Пример 3.

Исследовать сходимость ряда: .

Составим производящую функцию ряда . Вычислим:

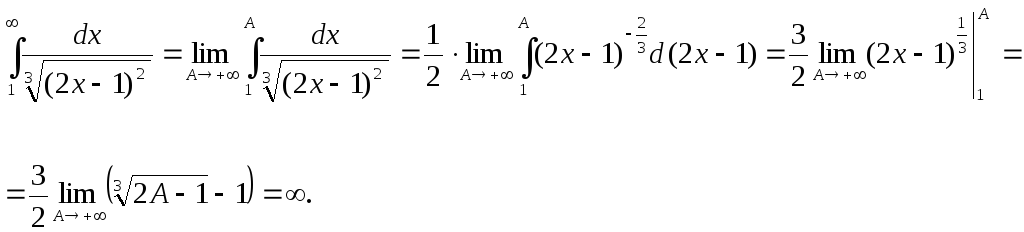
Несобственный интеграл расходится, расходится и данный ряд.