1.Я.С.Бугров, c.М. Никольский. Высшая математика: - т.2. Дифференциальное и интегральное исчисление. М., Наука (Дрофа). 2007.

Лекция 41. Ортогональные системы функций. Примеры ортогональных систем.

Основные понятия: ортогональные системы функций, ортогональный ряд, тригонометрическая система.

Из курса линейной алгебры известно, что если в линейном пространстве E конечной размерности выбрать базис, то любой элемент пространства E можно единственным образом разложить по выбранному базису и затем характеризовать конечным набором чисел - коэффициентами разложения, называемых координатами элемента в данном базисе. Если, кроме того, линейное пространство является евклидовым (это означает, что для элементов линейного пространство введено понятие скалярного произведения), то базис можно выбрать ортогональным.

Наиболее важными следствиями введения базиса являются два факта: 1) линейные операции или линейные преобразования над элементами линейного пространства эквивалентны линейным операциям (преобразованиям) над наборами координат элементов; 2) зная базис и координаты элемента легко восстановить сам элемент суммируя произведения координат на базисные векторы.

Эта идея – разложение элементов заданного множества по некоторой выбранной системе элементов – берется за основу при представлении сигнала, описываемого какой-то функцией, в виде ряда Фурье. Однако, те множества функций, которые ниже рассматриваются, будут бесконечномерными. Поэтому вместо конечных сумм возникают бесконечные, что делает теорию рядов Фурье, имеющую аналогии с разложениями в конечномерных евклидовых пространствах, более сложной.

Основным множеством функций, рассматриваемым ниже, будет множество функций кусочно-непрерывных на заданном отрезке Т. Напомним, что кусочно-непрерывной функцией на сегменте Т называется функция, которая непрерывна на нем всюду, за исключением конечного числа точек, в которых она имеет разрывы первого рода. В точке разрыва функции f считается (если не оговорено особо), что , где пределы функции f в точке справа и слева соответственно.

Множество кусочно-непрерывных функций образует линейное простанство со стандартно определенными операциями сложения функций и умножения функций на число. Кусочно-непрерывные функции интегрируемы. Интегрируемы их произведения и, в частности, квадраты функций.

В пространстве кусочно-непрерывных функций можно ввести понятие скалярного произведения. Скалярным произведением двух функций f(t) и g(t) называется число

.

Оно удовлетворяет всем аксиомам скалярного произведения. Таким образом, получаем евклидово пространство кусочно-непрерывных функций (но только бесконечномерное).

Определим норму (длину) элемента f как

.

Норма обладает следующими основными свойствами:

1. тогда и только тогда, когда во всех точках отрезка, за исключением, быть может, конечного числа точек;

2. , где α действительное число;

3. (неравенство треугольника).

Скалярное произведение позволяет определить понятие ортогональности функций. Две функции называются ортогональными, если их скалярное произведение равно нулю.

Система функций называется ортогональной на Т, если входящие в эту систему функции попарно ортогональны, т.е.

(1)

Если для всех n, то система называется ортонормированной.

Важность ортогональных систем определяется следующим обстоятельством. Пусть ряд

(2)

сходится на отрезке Т к функции f(t). Зафиксируем число n и умножим данный ряд на функцию . Если допустимо почленное интегрирование ряда, то, учитывая ортогональность системы , получим

.

Таким образом, коэффициенты ряда (2) вычисляются по формулам

, (3)

Наиболее простой вид формулы (3) имеют в случае, когда система ортонормирована. В этом случае

, (3^′)

Числа , найденные по формулам (3) или (3^′), называются коэффициентами Фурье функции f(t).

Как известно из курса математического анализа, почленное интегрирование ряда возможно лишь при выполнении определенных условий. Вместе с тем, формулы (3) имеют смысл для любой кусочно-непрерывной функции. Тем самым, для любой кусочно-непрерывной функции может быть записан ряд

~, (4)

где коэффициенты вычислены по формулам (3) или (3^′). Ряд (4) называется рядом Фурье функции f(t) по ортогональной системе функций .

Знак «~» в (4) означает, что числа являются коэффициентами Фурье функции f, то есть этот знак означает лишь определенную связь коэффициентов ряда с функцией. Сходимость ряда, тем более к функции f, заранее не предполагается.

Основные проблемы теории ортогональных рядов состоят в следующем: 1) при каких условиях ряд Фурье функции представляет ее (например сходится к ней); 2) в какой мере операции над функциями можно заменять операциями над ее коэффициентами Фурье?

Примерами ортогональных систем являются тригонометрическая система функций, система многочленов Лежандра, системы функций Радемахера, Уоллша и другие. Выбор конкретной системы зависит от решаемой задачи.

Литература к лекции 41

1. Я.С.Бугров, C.М. Никольский. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. –М.: Дрофа, 2007.

Лекции 43-45. Тригонометрические ряды. Разложение функций в ряды Фурье. Сходимость. Ряды Фурье для четных и нечетных функций. Преобразование Фурье.

Основные понятия: коэффициенты Фурье, ряд Фурье, преобразование Фурье, спектр функции, свертка функций.

Если функция имеет период , то тригонометрическим рядом Фурье функции на интервале называется ряд вида: , где , .

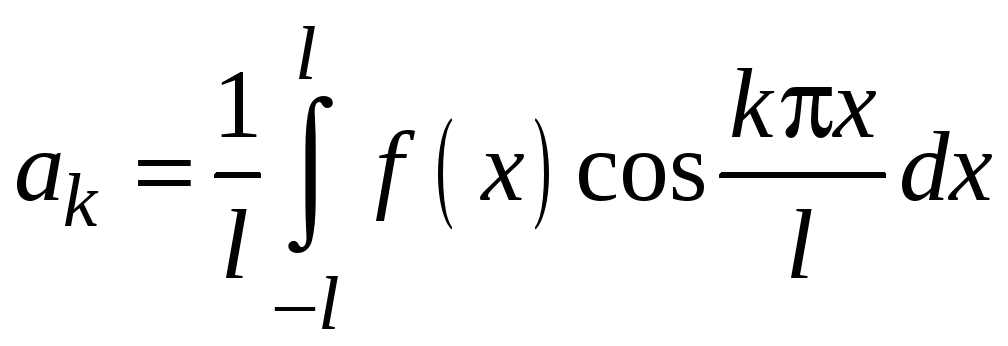При разложении в ряд Фурье следует учитывать, что для нечетной функции ( ) на симметричном интервале , а для четной функции () на симметричном интервале . Поэтому при разложении в ряд Фурье на симметричном интервале для нечетной функции имеем , а для четной функции имеем . Если функция общего вида, то нужно находить все коэффициенты. Кроме того, следует учесть, что , , .

Преобразование Фурье. Для абсолютно интегрируемой на всей прямой функции обозначим прямое преобразование Фурье. Если положить , то - обратное преобразование Фурье.

Заметим, что в литературе существует различие в определениях прямого и обратного преобразований Фурье, однако соответствующей заменой переменной их все можно свести к одному.

Косинус- преобразование Фурье определяется следующим образом:

.

Синус-преобразование Фурье определяется следующим образом:

.

Свертка Фурье двух абсолютно интегрируемых на всей прямой функций определяется следующим образом:.

Литература к лекциям 43-45.

1. Я.С.Бугров, C.М. Никольский. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. – М.: Дрофа, 2007.

12