18. Адреса. Доменная организация адресного пространства. Понятие о поддоменах и сверхдоменах.

IP-адреса нужны как для подключения новых пользователей к cети, так и для размещения информационных ресурсов. Количество задействованных в национальном сегменте интернета адресов и их географическое распределение характеризует степень проникновения интернет-технологий в повседневную жизнь страны.

В настоящее время в интернете используются два стандарта адресов: IPv4 и IPv6. В России второй стандарт по состоянию на конец 2005 года использовался только для построения опытных сетей. Поэтому мы сосредоточимся на распределении адресного пространства IPv4.

 Доменные зоны бывают как закрепленными географически, так и общемировыми. Сейчас мы с вами рассмотрим основные географические и мировые зоны доменов первого уровня.

   Дело в том, что каждое государство имеет закрепленное за ней доменное имя, а иногда этих зон за страной зарегистрировано две: одна – обозначение латиницей, другая – обозначение буквами национальных алфавитов. Доменное имя состоит их двух символов, которые представляют собой сокращение названия страны. К примеру, в России зарегистрировано две доменных зоны – .ru и .рф.

Домен — это адрес сайта в интернете. 

42. Статистические гипотезы. Нулевая и конкурирующая гипотезы. Проверка гипотезы о равенстве дисперсий двух нормально распределенных генеральных совокупностей по их оценкам. Параметрический критерий Стьюдента.

Пусть в (статистическом) эксперименте доступна наблюдению случайная величина X, распределение которой Р известно полностью или частично. Тогда любое утверждение, касающееся P, называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:

• Статистическая гипотеза, однозначно определяющая распределение P, то есть H:{P=P0}, где P0 какой-то конкретный закон, называется простой.

• Статистическая гипотеза, утверждающая принадлежность распределения P к некоторому семейству распределений, то есть вида H:{P∈р}, где р — семейство распределений, называется сложной.

На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу H0. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза H1, называемая конкурирующей или альтернативной. Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу. В большинстве случаев статистические критерии основаны на случайной выборке (X1,X2,..Хn) фиксированного объема ≥ 1 из распределения P. В последовательном анализе выборка формируется в ходе самого эксперимента и потому её объем является случайной величиной.

Проверка гипотезы о равенстве дисперсий двух нормальных генеральных совокупностей

Рассмотрим две случайные величины Х и У, каждая из которых подчиняется нормальному закону с дисперсиями. Пусть из этих генеральных совокупностей извлечены две выборки объёмами n1 и n2 . Проверим гипотезу Н0 о том

, что относительно альтернативной гипотезы Н1 , заключающейся в том, что

Однако, мы располагаем только выборочными дисперсиями

=и=Задача проверки гипотезы Н0 сводится к сравнению выборочных дисперсий. Для построения критической области с выбранной надёжностью необходимо исследовать совместный закон распределения оценок

и . Таким законом распределения является распределение Фишера – Снедекора (или F- распределение). Рассмотрим случайную величину х , распределённую нормально с математическим ожиданием Х и с дисперсией. Произведём две независимые выборки объёмами n1 и n2 . Для оценкииспользуют выборочные дисперсии. Случайную величину, определяемую отношением

, называют величиной с распределением Фишера-Снедекора. Имеются таблицы для дифференциального закона распределения Фишера-Снедекора, которые зависят лишь от объёма выборки и уровня значимости

, где k1=n1-1, k2=n2-1.

Вернёмся снова к задаче проверки гипотезы о равенстве дисперсий. Сначала нужно вычислить выборочные дисперсии. Найдём отношение , причём в числителе поставим большую из двух оценок дисперсии. Выберем уровень значимости a(альфа) и из таблиц находим число F

которое сравнивается с вычисленным F. Если окажется, что

, то проверяема гипотеза Н0 отвергается, в противном случае делается вывод о том, что наблюдения не противоречат проверяемой гипотезе.

t-критерий Стьюдента — общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках. t-статистика строится обычно по следующему общему принципу: в числителе случайная величина с нулевым математическим ожиданием (при выполнении нулевой гипотезы), а в знаменателе — выборочное стандартное отклонение этой случайной величины, получаемое как квадратный корень из несмещенной оценки дисперсии. Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями. Требование нормальности распределения данных является необходимым для точного t-теста. Однако, даже при других распределениях данных возможно использование t-статистики. Во многих случаях эта статистика асимптотически имеет стандартное нормальное распределение — N(0,1), поэтому можно использовать квантили этого распределения. Однако, часто даже в этом случае используют квантили не стандартного нормального распределения, а соответствующего распределения Стьюдента, как в точном t-тесте. Асимптотически они эквивалентны, однако на малых выборках доверительные интервалы распределения Стьюдента шире и надежнее.

43. Генеральная и выборочная совокупности. Объём выборки, репрезентативность выборки. Точечные оценки параметров распределения. Характеристики положения: среднее арифметическое, медиана, мода, наибольший и наименьший элемент выборки.

Генеральной совокупностью называется множество всех мыслимо возможных наблюдений, которые могли бы быть сделаны при данном реальном комплексе условий или более строго: генеральной совокупностью называется случайная величина x и связанное с ней вероятностное пространство {W,Á,Р}. Распределение случайной величины x называют распределением генеральной совокупности (говорят, например, о нормально распределенной или просто нормальной генеральной совокупности). Например, если производится ряд независимых измерений случайной величины x,то генеральная совокупность теоретически бесконечна (т.е. генеральная совокупность - абстрактное, условно - математическое понятие); если же проверяется число дефектных изделий в партии из N изделий, то эту партию рассматривают как конечную генеральную совокупность объема N. Выборочной совокупностью или просто выборкой объема n называется последовательность х1, х2, …, хn независимых одинаково распределенных случайных величин, распределение каждой из которых совпадает с распределением случайной величины x(Выборочной совокупностью называют часть отобранных объектов из генеральной совокупности). Например, результаты n первых измерений случайной величины x принято рассматривать как выборку объема n из бесконечной генеральной совокупности. Полученные данные называют наблюдениями случайной величины x, а также говорят, что случайная величина x "принимает значения" х1, х2, …, хn.

Объём выборки — число случаев, включённых в выборочную совокупность. Из статистических соображений рекомендуется, чтобы число случаев составляло не менее 30—35.

Модой случайной величины называется её наиболее вероятное значение. Термин «наиболее вероятное значение», строго говоря, применим только к прерывным величинам; для непрерывной величины модой является то значение, в котором плотность вероятности максимальна. Условимся обозначать моду буквой М . На рис.показана мода соответственно для прерывной и непрерывной случайных величин.

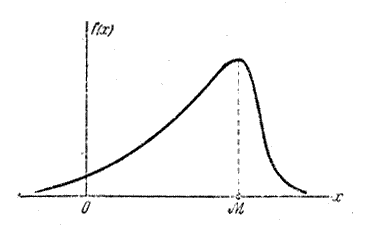
Медиана - возможное значение признака, которое делит ранжированную совокупность (вариационный ряд выборки) на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана.Медиана является важной характеристикой распределения случайной величины,может быть использована для центрирования распределения. При нечетном количестве вариантов медиана рассчитывается по формуле , а при четном

сре́днее арифмети́ческое — одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех зафиксированных значений, деленную на их количество.

наибольший(наименьший) элемент выборки - это такой элемент выборки, который принимает наибольшее(наименьшее) значение из всех элементов.

Рассматривая значения количественного признака как независимые случайные величины, можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения - это значит найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра. Итак, статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям: оценка должна быть несмещенной, эффективной и состоятельной.Поясним каждое из понятий.

Несмещенной называют статистическую оценку Q*, математическое ожидание которой равно оцениваемому параметру Q при любом объеме выборки, т. е.M(Q*) = Q.

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки п) имеет наименьшую возможную дисперсию.

Состоятельной называют статистическую оценку, которая при п->¥ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при п->¥ стремится к нулю, то такая оценка оказывается и состоятельной. Рассмотрим точечные оценки параметров распределения, т.е.оценки, которые определяются одним числом Q* =f( x1, x2,…,xn), где x1, x2,…,xn- выборка.

44. Характеристики рассеяния: размах вариации, среднее абсолютное отклонение, выборочная дисперсия, исправленная дисперсия, стандартное (среднеквадратичное отклонение), их соответствие параметрам генеральной совокупности.

Вариа́ция — различие значений какого-либо признака у разных единиц совокупности за один и тот же промежуток времени.

Размах вариации -разница между максимальным и минимальным значением.

. Размах вариации показывает только крайние отклонения признака и не отражает отдельных отклонений всех вариантов в ряду.Он характеризует пределы изменения варьирующего признака и зависим от колебаний двух крайних вариантов и абсолютно не связан с частотами в вариационном ряду, т.е. с характером распределения, что придает этой величине случайный характер.

Среднее абсолютное отклонение, или просто среднее отклонение (MAD – mean absolute deviation) — величина, используемая для оценки прогнозных функций.Этот показатель характеризует меру разброса значений совокупности данных вокруг их среднего значения.Абсолютным оно является потому, что суммируются отклонения по модулю, так как в противном случае сумма всех разбросов была бы равна нулю.

m(X)- одно из средних значений совокупности данных; это может быть среднее арифметическое (х, сверху черточка), но чаще всего в качестве среднего значения берется медиана.

xi- элемент совокупности данных

n – количество значений в анализируемой совокупности данных

∑-сумма

Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения , вводят сводную характеристику- выборочную дисперсию. Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .Если все значения признака выборки различны, то

если же все значения имеют частоты n1, n2,…,nk, то

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равноДля исправления выборочной дисперсии достаточно умножить ее на дробьполучим исправленную дисперсию S2( в квадрате). Исправленная дисперсия является несмещенной оценкой. В качестве оценки генеральной дисперсии принимают исправленную дисперсию.

Для оценки среднего квадратического генеральной совокупности используют исправленное среднее квадратическое отклонение Замечание: формулы для вычисления выборочной дисперсии и исправленной дисперсии отличаются только знаменателями. При достаточно больших n выборочная и исправленная дисперсии мало отличаются, поэтому на практике исправленной дисперсией пользуются, если n<30.

45. Числовые характеристики непрерывной случайной величины. Нормальное статистическое распределение случайных величин. При введении понятия математического ожидания воспользуемся понятием элемента вероятности р(х)(треугольник дельта) х.Предположим, что все возможные значения случайной величины Х принадлежат отрезку [а, b]. Разобьем произвольным образом этот отрезок точками а=x0<x1<x2<…<x_n=b на n частичных отрезков. В каждом таком частичном отрезке, длина которого (дельта треугольник)х, произвольно возьмем точку h_i, где i=l, 2, 3, ..., n. Известно, что вероятность попадания значения непрерывной случайной величины на отрезок (дельта)х приближенно равна р(х)(дельта)x (элемент вероятности) и поэтому приближенно будем считать, что случайная величина Х может принять n значений h_i на отрезке [а, b] с вероятностями р(h_i) (дельта)x_i. Теперь можно воспользоваться формулой, задающей математическое ожидание для дискретной случайной величины. В результате будем иметь.

Переходя к пределу в правой части равенства, имеем:

Математическим ожиданием M(X) непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называется определенный интеграл

Если возможные значения случайной величины распределены по всей оси Ох, то

Здесь предполагается, что несобственный интеграл сходится абсолютно, т. е. существует.

Т.к. дисперсия случайной величины есть математическое ожидание квадрата отклонения случайной величины от своего математического ожидания, то: дисперсией непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называется определенный интеграл

При вычислении дисперсии НСВХ также можно пользоваться формулой

Среднее квадратическое отклонение равно корню квадратному из дисперсии :

Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами А и , если ее плотность вероятности имеет вид:

где параметр μ — математическое ожидание, медиана и мода распределения, а параметр σ — стандартное отклонение (σ² — дисперсия) распределения. Кривую нормального закона распределения называют Нормальной или Гауссовой кривой.На рис. приведены нормальная кривая Р(Х) с параметрами А и и график функции распределения случайной величины Х, имеющей нормальный закон

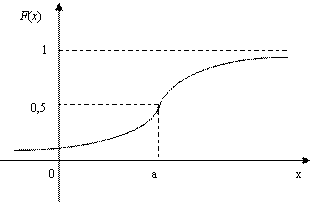
Характеристическая функция нормального распределения имеет вид:

Для вычисления вероятности того, что нормально распределенная случайная величина X будет принимать значения в промежуткеиспользуется формула

Ф₀ - функция Лапласа(значения берутся из таблиц)

48. Общие понятия теории вероятности и математической статистики. Случайные события и случайные величины, их классификация. Ожидаемые события. Частоты и относительные частоты ожидаемых событий. Вероятность. Классическое и статистическое определения вероятности.

Теория вероятностей изучает объективные закономерности массовых случайных событий. Она является теоретической базой для математической статистики, занимающейся разработкой методов сбора, описания и обработки результатов наблюдений. Путем наблюдений (испытаний, экспериментов), т.е. опыта в широком смысле слова, происходит познание явлений действительного мира. В своей практической деятельности мы часто встречаемся с явлениями, исход которых невозможно предсказать, результат которых зависит от случая. Случайное явление можно охарактеризовать отношением числа его наступлений к числу испытаний, в каждом из которых при одинаковых условиях всех испытаний оно могло наступить или не наступить.Теория вероятностей есть раздел математики, в котором изучаются случайные явления (события) и выявляются закономерности при массовом их повторении. Математическая статистика - это раздел математики, который имеет своим предметом изучения методов сбора, систематизации, обработки и использования статистических данных для получения научно обоснованных выводов и принятия решений. При этом под статистическими данными понимается совокупность чисел, которые представляют количественные характеристики интересующих нас признаков изучаемых объектов. Статистические данные получаются в результате специально поставленных опытов, наблюдений.Статистические данные по своей сущности зависят от многих случайных факторов, поэтому математическая статистика тесно связана с теорией вероятностей, которая является ее теоретической основой.

Одним из основных понятий теории вероятностей является понятие события. Под событием понимают любой факт, который может произойти в результате опыта или испытания. Под опытом, или испытанием, понимается осуществление определённого комплекса условий.Примеры событий:

– попадание в цель при выстреле из орудия (опыт — произведение выстрела; событие — попадание в цель);

– выпадение двух гербов при трёхкратном бросании монеты (опыт — трёхкратное бросание монеты; событие — выпадение двух гербов);

Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия заданному, отказ одного из звеньев автоматизированной системы управления.Случайные величины могут принимать дискретные, непрерывные и дискретно-непрерывные значения. Соответственно случайные величины классифицируют на дискретные, непрерывные и дискретно-непрерывные (смешанные). На схеме испытаний может быть определена как отдельная случайная величина (одномерная/скалярная), так и целая система одномерных взаимосвязанных случайных величин (многомерная/векторная).Пример смешанной случайной величины — время ожидания при переходе через автомобильную дорогу в городе на нерегулируемом перекрёстке. В бесконечных схемах (дискретных или непрерывных) уже изначально элементарные исходы удобно описывать количественно. Например, номера градаций типов несчастных случаев при анализе ДТП; время безотказной работы прибора при контроле качества и т. п. Числовые значения, описывающие результаты опытов, могут характеризовать не обязательно отдельные элементарные исходы в схеме испытаний, но и соответствовать каким-то более сложным событиям.Событием называется любой факт, который в результате опыта может произойти или не произойти. Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи. С событиями связываются некоторые числа, характеризующие степень объективной возможности появления этих событий, называемые вероятностями событий.

Определение и классификация случайных величин.

Под случайной величиной понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение. Возможные значения случайной величины образуют множество Ξ, которое называется множеством возможных значений случайной величины. Обозначения случайной величины: X, Y, Z; возможные значения случайной величины: x, y, z.В зависимости от вида множества Ξ случайные величины могут быть дискретными и недискретными. СВ Х называется дискретной, если множество ее возможных значений Ξ – счетное или конечное. Если множество возможных значений СВ несчетно, то такая СВ является недискретной.

Достоверным называется событие W, которое происходит в каждом опыте.Невозможным называется событие Æ, которое в результате опыта произойти не может.Несовместными называются события, которые в одном опыте не могут произойти одновременно. Суммой (объединением) двух событий A и B (обозначается A+B, AÈB) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.Произведением (пересечением) двух событий A и B (обозначается A×B, AÇB) называется такое событие, которое заключается в том, что происходят оба события A и B вместе.

Классическое определение вероятности: вероятность события определяется по формуле

где n - число элементарных равновозможных исходов данного опыта; m - число равновозможных исходов, приводящих к появлению события.

49. Статистические гипотезы. Нулевая и конкурирующая гипотезы. Непараметрические критерии: знаков, Ван-дер Вардена, Уилкоксона. Пусть в (статистическом) эксперименте доступна наблюдению случайная величина X, распределение которой Р известно полностью или частично. Тогда любое утверждение, касающееся P, называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:

• Статистическая гипотеза, однозначно определяющая распределение P, то есть H:{P=P0}, где P0 какой-то конкретный закон, называется простой.

• Статистическая гипотеза, утверждающая принадлежность распределения P к некоторому семейству распределений, то есть вида H:{P∈р}, где р — семейство распределений, называется сложной.

На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу H0. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза H1, называемая конкурирующей или альтернативной. Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу. В большинстве случаев статистические критерии основаны на случайной выборке (X1,X2,..Хn) фиксированного объема ≥ 1 из распределения P. В последовательном анализе выборка формируется в ходе самого эксперимента и потому её объем является случайной величиной.

ВАН ДЕР ВАРДЕНА КРИТЕРИЯ

непараметрический критерий однородности двух выборок  основанный на ранговой статистике

где - ранги (порядковые номера) случайных величин в общем вариационном ряду из  и , функция определяется заранее выбранной подстановкой 

- обратная функция нормального распределения с параметрами (О, 1). Выбор подстановки определяется тем, что для заданной альтернативной гипртезы мощность критерия должна быть наибольшей.

Т-критерий Вилкоксона — непараметрический статистический тест (критерий), используемый для проверки различий между двумя выборками парных измерений. Впервые предложенФрэнком Уилкоксоном

Критерий предназначен для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить не только направленность изменений, но и их выраженность, то есть способен определить, является ли сдвиг показателей в одном направлении более интенсивным, чем в другом.

U=R-(n1(n1+1)/2) формула уинкинсона