Задание № 2. Определить вид отношения между понятиями. Выразить в логической форме и изобразить в круговой схеме

1) Строитель - житель города.

2) Плоская замкнутая геометрическая фигура - треугольник - прямоугольник - треугольник

Задание № 3. Произвести обобщение понятий: циркулярная коммуникация, рекламный текст

Для того чтобы произвести обобщение понятия, необходимо исключить его видовые признаки и оставить родовые. Тем самым, в конечном итоге обобщения у нас остается большой объем этого понятия, но с меньшим содержанием. Итак,

1) Циркулярная коммуникация коммуникация передача информации информация.

2) Рекламный текст текст.

Задание № 4. Определить вид деления, и какое правило нарушено, если нарушено

1) Социальные революции могут быть мирными и не мирными.

Вид деления - дихотомия. Правила не нарушены.

2) Приговор бывает справедливым, несправедливым и обвинительным.

Нарушено правило «соразмерность в делении». В данном нет полного деления, оно с остатком. Верное деление будет звучать примерно так: Приговор бывает справедливый и несправедливый, обвинительный и оправдательный. Вид такого деления - политомия.

Заключение

Изучение законов и форм мышления помогает человеку сознательно применять их в процессе познания с целью воздействия на окружающий мир и его преобразования.

Значение науки логики заключается в том, что она является основой формирования научного аппарата - системы понятий в сфере научных исследований на уровне теоретического мышления, а также и в учебном процессе для раскрытия сущности изучаемых общих понятий различных дисциплин, для осуществления преемственности понятийного аппарата изучаемых наук.

Мыслить логично - это значит мыслить точно и последовательно, не допуская противоречий в своих рассуждениях, уметь вскрывать логические ошибки. Эти качества мышления имеют большое значение в любой области юриспруденции, требующей точности мышления, обоснованности выводов. Так, например, приговор суда должен основываться на тщательно проверенном фактическом материале. Для правильного судебного решения важное значение при разбирательстве дела имеет также убедительность, логическая стройность речи прокурора и защитника.

25. Семантические таблицы истинности.

Семантические таблицы для классической логики. От таблиц истинности к семантическим таблицам

Рассмотрим построение таблицы истинности пропозициональной формулы ( A ? B ? C ) ? ( A ? B ) ( см. табл. 9.1). Анализируя таблицу, можно отметить, что большинство информации в ней избыточно. Таблицу можно значительно сократить, пользуясь следующими правилами: для истинности дизъюнкции достаточно истинности одного из членов; для ложности конъюнкции достаточна ложность одного из членов; истина следует из всего что угодно; из лжи следует все что угодно. Сокращенная таблица истинности показана на табл. 9.2 .

A	в	с	в v с	Л =>¦ В V с	л=> в	Формула
1	1	1	1	1	1	1
1	1	0	1	1	1	1
1	0	1	1	1	0	0
1	0	0	0	0	0	1
0	1	1	1	1	1	1
0	1	0	1	1	1	1
0	0	1	1	1	1	1
0	0	0	0	1	1	1

Таблица 9.1: Полная таблица истинности

При таком сокращении самым тонким местом является проверка того, что ни один случай не упущен. Можно создавать много способов сокращения таблиц истинности, но в некотором смысле все это будет изобретением велосипеда, поскольку, базируясь на правилах сокращения, голландский логик Бет (Е. W . Beth ) создал в 50-х годах формализм, гарантирующий полноту разбора и выполняющий все прямые сокращения. Он основан на необходимых и достаточных условиях истинности и ложности формул. Начнем с примера для той же формулы.

Л	в	с	в v с	Л =>¦ В V с	л =>¦ в	Формула
0	—	—	—	1	1	1
1	1	—	1	1	1	1
1	0	0	0	0	0	1
1	0	1	1	1	0	0

Таблица 9.2: Сокращенная таблица истинности

Ищем все возможные случаи, когда формула ложна. Если таковых не найдется, то она истинна. Наша формула представляет собой импликацию, импликация ложна, если ее посылка истинна, а заключение ложно. Получаем следующее преобразование:

=| ( А => • В V С )=> • ( А => • В ) |=А => В V С (9.1)Ч ( Л ^ В )

После применения аналогичного преобразования к третьей формуле получаем

=| ( А => В V С )=> ( А => В ) |=А => В V С =|( А => В ) (9.2)\=А =\ В

Теперь приходится рассматривать условия истинности импликации. Бет оптимально подобрал два случая, исчерпывающих все возможности, когда импликация истинна: необходимо и достаточно, чтобы A было ложно либо B истинно. То, что мы разбираем два независимых случая, отражается разбиением таблицы на подтаблицы, в которых общее лишь то, что было получено до разделения. После разбиения импликации аналогично разобьется и дизъюнкция.

Здесь в двух из трех образовавшихся подтаблиц встретились проти­воречия; такие подтаблицы называются закрытыми и отмечаются двойной чертой. Оставшаяся подтаблица выдала тот единственный набор значений, при котором формула ложна: A истинно, B ложно и C истинно. Итак, мы получаем следующий метод проверки истинности форму­лы либо построения контрпримера. Предполагаем, что формула ложна. Строим семантическую таблицу и, если все ее подтаблицы закрылись, приводим предположение о ложности формулы к абсурду и делаем вывод, что она истинна. Иначе незакрытая подтаблица дает контрпример.

Правила разбиения формул в семантических таблицах

Просуммируем правила разбиения для связок логики высказываний.

Если в правиле нижняя часть не разделена, результирующие формулы остаются в той же подтаблице, в противном случае они распределяются по двум новым подтаблицам, которые далее развиваются независимо. Значит, подтаблицы семантической таблицы образуют бинарное дерево.

Теперь остается заняться практикой и не забывать, что в любом доказательстве правильная общая структура значит не меньше, чем правильность отдельных шагов. Хорошо и то, что любая последовательность правильных шагов приводит к результату, хотя, конечно, удачный выбор порядка разбиений может сильно сократить таблицу.

Упражнения к § 9.2

9.2.1. Мы научились проверять на семантических таблицах высказывания на тождественную истинность. А как их проверять на тождественную ложность? Что в этом случае даст незакрытая семантическая таблица?

Проверить на семантических таблицах высказывания и рассуждения.

• ( А => • В У С ) => • ( А => • В ) У ( А => • С )

• ( А => • В ) У ( А => • С ) => • ( А => • В У С )

• ( А & В => • С ) => • ( А => • С ) V ( . В =>• С )

• ( А => • С ) V ( . В =>• С ) => • ( А & В => • С )

• ( ASz ( B У С )) => • ( AfcC ) V ( BSzC )

• (Afc(I? V С )) => • (AfcC) V (ASzB)

• (ASzB) V (A&C) => (Afc(I? V C))

• ((A => B) => (C => Z))) => (A => C)Sz(D => B)

• ((A => B) =^ C) => i V ( В ^> C)

• A V (B 4 C) =^ ((A => B) => C)

• (A V (B&C)) => (A V B)&(A V C)

• (A V B)&(A V C) ^> (A V (BSzC))

• (A V B ) Sz ( A У С ) => В У С

• В У С => (А У B ) Sz ( A У С )

• ( А => B)Sz(A => C)Sz(A => D) => А

• ( В => А )&( С => A)Sz(D => А ) => А

• ( А => • В V C)Sz(B => • A)Sz(C => D)Sz(D => В ) => (A => i?)

• (AfcZ) 4 В V C) 4 (A => B) V (A => C) V (Z) => B)

• (A => I? V C)&(­A =4> C) 4 В V С

• ((A => • С ) => • D)Sz­D => • A&­C

• (A => B)lk(B => С ) => (Л => C)

Майор Тронин в результате расследования установил, что два сотрудника организации п/я № 13 являются агентами. Медников — агент английский либо американский, а Иванов — английский ли­бо израильский. С присущей ему проницательностью тов. Тронин сделал вывод, что п/я № 13 находится под контролем “ Intelligence Service ”. Прав ли он?

Если в России пытаются проводить реформы, то начинается смутное время. Если начинается смутное время, то либо наступает гражданская война, либо иностранное нашествие, либо Россия теряет часть территорий. Если наступает гражданская война, то население испытывает ужасные бедствия. Не лучше приходится на­селению и при нашествии. Сейчас в России пытаются проводить реформы. Значит, российский народ ждут ужасные бедствия.

( L . Carroll *) Он никогда не поет больше часа. Если кто-то поет больше часа, он надоедает окружающим. Тот, кто не надоедает окружающим, — желанный гость. Значит, он — желанный гость.

Создайте правила разбиения для эквивалентности и на их основе постройте семантическую таблицу для (( А 43> В ) 43> С ) 43> ( А - фф- ( В - фф- С )).

( J . Venn ) Существовал клуб с такими правилами:

• Члены финансового комитета должны избираться среди членов общей дирекции.

• Нельзя быть одновременно членом общей дирекции и членом библиотечного комитета, не будучи членом финансового комитета.

• Ни один член библиотечного совета не может быть членом финансового комитета.

Упростите правила.

Семантические таблицы с кванторами

отличие от таблиц истинности, метод семантических таблиц обобща­ется на всю логику предикатов. Здесь техническое улучшение, которым казалось исключение лишних случаев из перебора, переходит в прин­ципиальное. Это — типичная ситуация в истории науки. Стремление улучшить изложение какого-то темного места гораздо чаще приводит к принципиальным открытиям, чем амбициозные попытки перевернуть науку и создать какую-либо “общую теорию всего”. Теория относительности была создана Эйнштейном в результате доводки до логического конца анализа электродинамики движущихся тел, общая теория относительности также почти как техническое улучшение интенсивно ведшихся в то время многими крупными учеными работ по применению тензорных методов к механике. А вот все его многолетние усилия со­здать общую теорию поля не привели ни к чему. Лобачевский создал неевклидову геометрию, пытаясь усовершенствовать изложение геометрии для исключительно тупого контингента слушателей, примерно соответствующего нынешнему факультету повышения квалификации 1.

Рассмотрим условия истинности и ложности всеобщности и существования. Поскольку Ух А истинна тогда и только тогда, когдаА ( с ) истинно для любого конкретного с, мы, имея |=Ух А, можем получитьA ( ci ) всякий раз, когда в таблице либо подтаблице появляется объект сне сли же =|Ух А, то мы знаем лишь, что существует такой объ­екта, для которогоА{а) ложно. Чтобы отобразить это, постулируем =|А{с п +\ ) для нового, ранее в таблице не встречавшегося, объектас п +\ (называемоговспомогательной константой). Таким образом, приходим к следующим правилам разбиения для кванторов.

|= Ух А = |Ух А

|= А ( а ) =\ А ( с п +1 ) (9.4)

| = Эх А =\ Зх А |=А ( с п +1 ) =|А { а )

• 1 Известно, что нет ничего легче, как не задумываясь ответить на вопрос. Один дурак, при наличии эрудиции либо уверенности в себе, может ответить на столько вопросов, что сто умных не смогут задать.

Рассмотрим пример: проверка формулы

Эх А ( х )$ г ; Ух В ( х ) => •Эх ( A ( x ) SzB ( x )). =\ Эх А ( х )$ г ; Ух В ( х ) => •Эх ( A ( x ) SzB ( x )) |=Эх А ( х ) кУх В ( х ) =|Эх { А ( х ) кВ ( х )) |=Эх А ( х ) |=A ( ci ) (9.5)

|= Ух В ( х ) \= В ( С 1 ) =\ ( A ( c i ) fe ^ ( c i )) = |А ( С 1 ) | = | Д ( С 1 )

В дальнейшем для единообразия вспомогательные константы обозначаются с\, с 2 , ¦¦¦ Мы ввели объектс\, рассмотрев |=Эх А ( х ), после чего подставили его в две другие кванторные формулы. Следующий пример показывает, что не всегда удается обойтись одним объектом.

=| Ух ( А ( х ) VВ ( х )) => •Ух А ( х ) VУх В ( х ) =\ Ух А ( х ) VУх В ( х ) \= Ух ( А ( х ) У В ( х ))

=\ Ух А ( х ) =\ Ма ) =\ V xВ ( х ) (9.6)

=1 вы |=A(ci) VB(ci)

1=	А ( с 2 ) VВ ( с 2 )
1 =A( Cl )	|= B(ci)
	\= А ( с 2 ) \= В { с 2 )

Здесь видно, что нам пришлось использовать |= Ух ( А ( х ) VВ{х)) дважды: дляс\ ис 2 . И именно из-за различия этих двух значений таблица не закрылась; незапертая подтаблица дает следующую опровергающую модель:

С \ с 2 А 0 1 В 1 О

Следующий пример иллюстрирует еще две особенности, возникающие в предикатных семантических таблицах: возможность бесконечного порождения констант и аномалия с первым объектом. Он заодно показывает, что незапертость подтаблицы приходится порою усматривать более или менее косвенно, а не устанавливать доведением построения до конца, и что одна и та же формула может использоваться бесконечное количество раз.

=| Ух Эу А ( х , у ) => •Эх А ( х , х ) =\ Эх А ( х , х ) \=УхЗуА(х,у) \= ЭуА ( с 1, у ) \= А ( а , с 2 ) , „ _.

=| А { с \, С \) |=Эу А ( с 2, у ) |=А ( с 2 , сз ) =\ А ( с 2, сг )

Итак, бесконечно порождаются новые константы а, для которых выполнено |= A ( ci , Ci + i ), но =|A ( ci , Ci ). Немного разобравшись с анализи­руемой формулой, мы видим, что построенная опровергающая модель отнюдь не минимальная. Достаточно было бы рассмотреть множество из двух элементов.

Упражнения к § 9.3

Проверить на семантических таблицах высказывания и рассуждения.

[ К ] Некоторые цыплята — кошки. Некоторые кошки знают французский язык. Значит, некоторые цыплята знают французский.

Эх ( А ( х ) =>Уу А ( у )) 2 .

Ух ( А VВ ( х )) => •А VУх В ( х ).

2 Р. Смальян прокомментировал это высказывание следующим анекдотом. Заходит ковбой в бар и говорит бармену: “Мне налей и всем налей. Такой уж я человек: когда я пью, все пьют”. Через некоторое время: “Мне повтори и всем повтори. Такой уж я человек: когда я пью, все пьют”. Затем кладет на стойку деньги: “С меня возьми и со всех возьми. Такой уж я человек: когда я плачу, и все платят”.

Ух {А(х) VВ ( х )) => ¦Эх А ( х ) VУх В ( х ).

Зх А(х)$г;Ух (A ( x ) VВ ( х )) => ¦Эх В ( х ).

Зх A ( x ) Sz 3 x В ( х ) => • Ух ( А ( х ) V В ( х )).

• 93.1. yxA(x)Sz3xC(x)Sz3xB(x) => • 3x(A(x)SzB(x)SzC(x)).

• Зх ( A ( x ) SzB ( x )) =>• Зх А(х)$г;Ух В ( х ).

• (ЗхА(х) =>• \/ж.В(ж)) =>• \/ж(-А(ж) =>• - В ( ж )).

• 3 x ( A ( x ) => ¦ -В ( ж )) => ¦ ЗжА(ж)&\/ж.В(ж).

• УхЗуА(х,у)&3хУуВ(х,у) =>ЭхЭу ( А ( х , у )$ г ; В ( х , у )).

• Ух(А(х) V В ( х ))&( УхА ( х ) => • ЗжС(ж))&\/ж(-В(ж) =>• С ( х )) => ЗжС(ж).

• \/ж ( А ( х ) V - В ( ж ))& Зж ( А ( ж ) V С)&Зж(С =>• - б ( ж )) => ¦ Зж-В(ж).

• Ух(А(х) \/В(х))1кЗх­А(х)1к УхУу ( В ( х ) => • С ( г /))& Зж . О ( ж ) => • 3 x ( C ( x ) SzD ( x )).

• УхЗу ( А ( х ) =>¦ B ( y )) Sz (3 xA ( x ) => С ) => ( С => 3 zB ( z )).

• УхУу ( А ( х ) => • B ( y )) Sz (3 xC ( x ) => • ЗжА ( ж ))& Зж (С ( ж ) => • - В ( ж )) => Зж - В ( ж ).

• (3 xA ( x ) => УуВ(х,у)) УУх­А(х).

• УхЗу ( А ( х ) => ¦ В ( у )) => • (\/ж-А(ж) =>• Зж-В(ж)).

• \/ж(Л(ж) => 5( ж ))& Зж (. В ( ж )&С ( х )) => • Зж (. В ( ж )&А ( ж )).

• (Зж-В(ж) V ЗжС ( ж ))& Ух(С(х) => В{х)) => ЗхВ(х).

• Ух ( С ( х ) => • B ( x ) SzD ( x )) Sz Зх(А(х)кС(х)) => Зх ( А ( х ) кВ ( х )).

• [ К ] Некоторые птицы, гордящиеся своим хвостом, не могут петь. Ни одна птица, кроме павлина, не может гордиться своим хвостом. Значит, некоторые павлины не могут петь.

• [ K ] Все львы свирепы. Некоторые львы не пьют кофе. Следовательно, некоторые из тех, кто пьет кофе, не свирепы.

• [ K ] Ни одно ископаемое животное не может быть несчастно в любви. Устрица может быть несчастна в любви. Следовательно, некоторые устрицы — не ископаемые животные.

• [ K ] Золото тяжелое. Ничто, кроме золота, не может заставить его замолчать. Следовательно, ничто легкое не может заставить его замолчать.

• Некоторые лампочки плохо светят. Лампочки предназначены для того, чтобы светить. Следовательно, некоторые вещи, предназначенные для того, чтобы светить, светят плохо.

• [ K ] Некоторые подушки мягкие. Ни одна кочерга не мягкая. Следовательно, некоторые кочерги — не подушки.

• [ K ] Лишь тот, кто храбр, достоин славы. Некоторые хвастуны — трусы. Следовательно, некоторые хвастуны недостойны славы.

• [ K *] Необразованные люди обо всем судят поверхностно. Среди студентов Удмуртского университета есть и образованные люди. Значит, некоторые студенты УдГУ не судят обо всем поверхностно.

• [ K *] Все козлята прыгают. Ни одно молодое животное не прыга­ет, если оно не здорово. Следовательно, все молодые козлята здоровы.

• Некоторые козы любят сено. Ни одна собака сена не любит. Значит, некоторые собаки — не козы.

• Те, кто что-то учил, решили некоторые задачи. Андрей не решил ни одной. Значит, он не учил ничего.

• Все рыбаки любители приврать. Все священники соблюдают заповеди. Никто не может и соблюдать заповеди, и вместе с тем врать. Значит, ни один рыбак не священник.

• Не все политики мошенники. Все мошенники умны. Значит, некоторые политики глупы. Сокращенные семантические таблицы

Рассмотрим случай, когда часть компонент в формуле избыточна. Построим таблицу для формулы

( A ? B ) & ( B ? D ) & ( D ? E ) ? ( B ? E ).

Студенты — любители покушать. Некоторые студенты худые. Не все те, кто любит покушать, студенты. Значит, некоторые лю­бители покушать не являются худыми студентами.

Все мафиози жестоки. Некоторые чеченцы жестоки. Следовательно, некоторые чеченцы — мафиози.

Все шутки для того и предназначены, чтобы смешить людей. Ни одно постановление Думы не является шуткой. Значит, ни одно такое постановление не предназначено для того, чтобы смешить людей.

Здесь видно, что разбор вариантов по первой импликации ничего не дал, иможно было начать сразусовторой, получив гораздо более приличную таблицу.

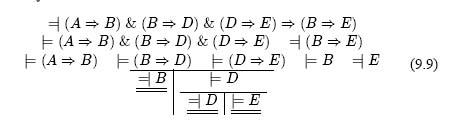
Но как это усмотреть в самой таблице? В таблице ( 9.8 ) еще до ее разбиения появилась формула |= B , которая получилась во втором варианте первого разбиения. Значит, в этом варианте ни одной новой формулы не появилось, и мы сделали пустой шаг3.

Определение 9.4.1. Шаг построения таблицы называется избыточным, если хотя бы в одной из получающихся подтаблиц не появляется новых формул, либо если разбивается формула |=Эх А ( х ), а в таблице уже имеется формула |=A ( cj ), либо разбивается = \ Ух А ( х ), ав таблицеуже имеется = \ A { ci ). Подтаблица называется финальной, если в ней не может быть сделано ни одного неизбыточного применения правил.

Избыточные разбиения просто не нужно делать. Более того, понятие избыточного разбиения позволило нам дать точный ответ на вопрос, когда же можно переходить к построению контрпримера: когда нашли финальную подтаблицу

На рассмотренных практических примерах видно, что иногда разбор при помощи семантических таблиц можно сократить далее. Например, если в подтаблице встречаются формулы |= А => В и |=А , то подтаблица с =|А сразу же закрывается, и нетривиальна лишь таблица с |=В .

Здесь без нарушения строгости и общности можно обойтись без раз- делениятаблицыи просто добавить |= B . Это правило сокращения формулируется следующим образом:

Modus Ponens — название этого правила в традиционной логике. Аналогично устанавливаются следующие правила сокращения:Modus Ponens — название этого правила в традиционной логике. Аналогично устанавливаются следующие правила сокращения:

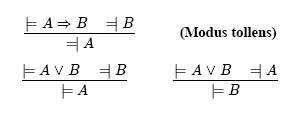
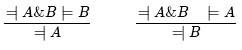
• 3 На самом деле ничуть не лучше и формула =| A , появившаяся в первом варианте, поскольку элементарная формула A больше нигде не встречается.

Еще один класс правил сокращения, применимых менее часто, это контрприменения, или обращения правил, не разбивающих таблицу. Например, имея |= А и |=В, можно заключить |=AlkB . Эти правила целесообразно применять для того, чтобы избежать разбиения таблицы по сложной формуле в ситуации, подобной следующей:

В отличие от предыдущих правил сокращения, которые являлись полностью безопасными, следующие правила сокращают лишь поиск опровержения, а при поиске доказательства заводят в тупик. Они основаны на наблюдении, что семантическая таблица с кванторами не всегда дает минимальную опровергающую модель. Избежать этого можно, разрешив подставлять в кванторные правила, в которых требуется новая константа, константу имеющуюся. Если при такой попытке подта-блица не закрылась, то мы находим опровергающую модель, если же закрылась, то попытка наша неудачна и нужно вернуться к стандартным правилам. Рассмотрим, как с помощью этого приема упрощается построение последней таблицы предыдущего параграфа.

=| УхЗу А ( х , у ) =>ЗхА(х, х ) =\ЗхА(х,х) \=\/хЗуА(х,у) \=3у А{с\,у) |=А{с\,С2) =\ А{с\,с\) (9.12)

|= Зу А ( с 2, у ) |=A ( c 2, ci ) Н ^( е 2 , е 2 )

А вот если взять в предпоследней строке с 2 вместо с\, наша таблица “закроется”.

Подытожим :

Если мы ищем доказательство, то нужно обязательно рас­сматривать все варианты, брать новые константы, но подстановки констант можно искать самые многообещающие, а не перебирать все подряд.

Если мы ищем опровержение, можно ограничиваться одним, самым бесперспективным с точки зрения противоречий вариантом, иногда брать старые константы вместо новых, но подстановки обязательно проделать все.

Работая в одном направлении (доказательство либо опровержение), нельзя слишком увлекаться приведенными выше послаблениями, поскольку и Ваша первоначальная оценка формулы как истинной либо опровержимой может оказаться неверной, и сама формула в реальных задачах может быть видоизменена, так как никакая формализация не отражает полностью содержания реальной задачи.

При оформлении готового решения эти послабления можно использовать вовсю.

Чаще всего разумно до разделения таблицы проделать все действия, которые можно выполнить без разделения.

В случае, если разбор случаев может быть заменен на пра­вило сокращения, это целесообразно сделать.

Избыточное разбиение формул делать не нужно.

Если в некотором варианте все разбиения избыточны, он готов для построения по нему опровергающей модели.

Упражнения к § 9.4

Проверить на семантических таблицах высказывания и рассуждения. Если заключение частично опущено, восстановите его сами.

9.4.1. (( А => •BSzC ) => •D ) Sz ( C => •В ) => •( А => • С).

9.4.2. ( А V В => • DSzC)Sz((A => • С ) => • E)Sz((A => D) => H)Sz(B => F) => E&zH&F.

9.4.3. ((A => В ) V ((A => В ) => С ) => D) => D.

9.4.4. (AvB=^ DSzC) => (A => C)Sz(A => D)Sz(B => D).

9.4.5. (A => C)Sz(A => D)Sz(B => D) => (A\/ В => DSzC).

9.4.6. (AvB=^ DSzC)Sz­A => B V С V D.

9.4.7. A V С V .D => (Afc­B => C)Sz(DSzB => C).

9.4.8. (ASzB => • D V С ) => • D V (C&A => • Z3).

9.4.9. (A V -B => • DSzC)Sz((A => C) => E)Sz((B => • Z)) => • ZZ)& (ESzH => • i* 1 ) => • i* 1 .

9.4.10. ((A => • D) => • E)Sz((D => A) => H)Sz(E \/ H =$¦ G \/ F) =$¦ G.

9.4.11. ( AvB =^ D )&( A У С => E )$> c (A =5- В У С ) => E У D .

9.4.12. (­A V ­-B V С У D) => (A => Z)) V (Z? => Z)) V (C => Z)).

9.4.13. (A => Z)&C)&((A => Z)) => Z?)&((A => C) => H)Sz(E У H => G) => G.

9.4.14. ((A => BSzC) => Z))&(A => Z3)&(Z?&A => C) => (E => Z)).

9.4.15. ((A => BSzC) => Z))&(AfcZ? => Z3)&(­Z?&A => C) => D.

9.4.16. ( ASzH => Z 3)&(HSzA => C )&(A =>D ) = з - В У С У D .

9.4.17. ( А => В У С У D ) Sz (( A =>D ) => Z ?)&(( A => С ) => Z ?) => Z?.

9.4.18. А => BSzC ) Sz ( B =>DSzE ) Sz ( C =>F ) Sz ( ESzF =>G ) Sz ( GSzD => ZZ ) => ( А => ZZ ).

9.4.19. \/ ж ( А ( ж )& В ( ж ))& Зж ( А ( ж )=> С ( ж ))& Зж (?>( ж )=> Z )(: r ))&

Уж ( С ( ж )&1)( ж )=>??( ж )) => Зж ?( ж ).

9.4.22. Зж ( А ( ж ) =>¦ Z 3( x ))& Vx ( A ( x ) V С )& Зж ( С ^ В ( ж )) => ЗжБ ( ж ).

9.4.23. ( Vi А ( ж ) =>¦ 3 xZ 3( x ))& Ух ( С ( х ) =>¦ А ( ж ))&\/ ж ( С ( ж ) V Z ?) =>

3 xZ 3( x ) V Z ).

9.4.24. \/ ж (- А ( ж ) => • Зж 5( ж ))&\/ ж ( С ( ж ) V А ( ж ))& Зх ( С ( х ) => • - В ( ж )) =>¦ 3 xZ 3(x).

9.4.25. УхЗу ( А ( х , у ) У В ( у , х ))$ г ; УхУу ( А ( х , у ) =>¦ С ( ж ))&

ЗхУу ( В ( х , у ) => • С ( ж )) =>¦ ЗжС ( ж ).

9.4.26. УхЗуА ( х , у ) кУхЗуА ( х , y ) kNxiy { A { x , у ) =? В { х )) к

УхУу {А ( х , у )^­{ х )) => Ух { Н ( х )^ В { х ) кС { х )).

9.4.27. УхЗуА ( х , у ) кЗхУу ( А ( х , у ) кВ { х ) =>С ( х , у )) к VzB ( z )=> ЗхЗуС ( х , у ).

9.4.28. УхЗуА ( х , у ) кУхЗу ( А ( х , у ) кВ ( х ) =>С ( х , у )) к УгВ ( г ) => ЗхЗуС ( х , у ).

9.4.29. Ух ( А ( х ) => 3y(B(y)kR(x,y)))kyx(A(x) => Vy(Q(y) =>

R{x,y)))k3xA(x) => 3x{­Q{x)kB(x)).

9.4.30. 3x(Q(x)kyy(B(y) => R(x,y))) => (Vx(Q(x) => - В ( ж )) =>¦ Зж ( Б ( ж )& Д ( ж , ж ))).

9.4.31. Зж (<5( ж ) & Зу { В { у ) к R ( x , y ))) к \/ г /( А ( г /) => • \/ ж (<5( ж ) =>¦R ( x , y ))) => • Зж(3( ж ).

9.4.32. \/ ж ( А ( ж ) => Vy ( Q ( y ) =? R { x , y ))) k 3 x { A { x ) k

Уу ( В ( у ) => R ( x , y ))) => Зх­Жх ) кВ ( х )).

9.4.33. Ух ( А ( х ) =>( ЗуВ ( х , у ) =>ЗуС ( х , у ))) к Ух ( ЗуВ ( х , у ) => В ( х , х )) к­ЗхВ ( х , х ) к

УхУу ( С ( х , у ) =>В ( у , х )) => Ух ( А ( х ) => Уу­В ( х , у )).

9.4.34. Ух ( Р ( а , х ) =>Q ( x , b )) k (3 yQ ( y , b ) =>3 yQ ( b , y )) =>

(3 zP ( a , z ) ^ Зж <3(6, ж )).

9.4.35. Ух ( А ( х ) =>yy ( Q ( y ) =>R ( x , y ))) к Ух ( А ( х ) =>Уу ( В ( у ) => Д ( ж , г /))) => ­\/ ж (- В ( ж ) => А ( ж )).

9.4.36. Если ездить на работу на автобусе, то приходится висеть на подножке или рискуешь опоздать. Если не ездить на нем, то надо ходить пешком. Если ходишь на работу пешком, то никогда не висишь на подножке, но можешь простудиться. Следовательно, если не рисковать опоздать, то надо висеть на подножке либо рисковать простудиться.

Если пойдешь в лес весной, тебя укусит клещ. Те, кого кусает клещ, заболевают энцефалитом или им делают укол. Тех, кто заболел, кладут в больницу. В больнице всегда делают уколы. Значит, если весной пойдешь в лес, ...

Будешь есть много хлеба, потолстеешь. Толстяки больны и вялы. Больные не могут добиться успеха, если им не повезет. Вялым людям никогда не везет. Значит, чтобы добиться успеха, необходимо.

Старательные люди добиваются успеха. Лишь тот может считаться старательным, кто работает не менее десяти часов в сутки. Нельзя одновременно работать и отдыхать по десять часов в сутки. Легкомысленные люди отдыхают не менее десяти часов в сутки. Следовательно, легкомысленные люди.

Розовая вода приятно пахнет. Ни одно лекарство не пахнет приятно. Если человек болен, он должен принимать лекарство либо соблюдать режим. Соблюдать режим и не принимать лекарство нельзя. Следовательно, если человек употребляет розовую воду, он не болен.

Если по телевизору не идет интересное кино, то в общежитии собирается веселая компания. Веселая компания всегда шумна. При шуме готовиться к занятиям невозможно. Если по телевизору идет интересное кино, невозможно не смотреть телевизор. Смотреть телевизор и готовиться к занятиям нельзя. Значит, в общежитии ...

Известно, что убийца — Джон, Билл или Джек. Если Джон или Джек—убийца, то убийство было после полуночи. Если убийство было до полуночи, то Джон лжет или Билл — убийца. Если Джон не лжет, то убийца — Билл. Следовательно, Билл — убийца или убийство было после полуночи.

Коля и Вася никогда не бывают вместе. Маша придет на вечеринку только вместе с Колей, Вася — только вместе с Глашей. Вечеринка веселая, только если на ней присутствуют и Маша, и Глаша. Значит, веселых вечеринок не бывает.

9.4.44. Все парни самолюбивы. Ни один самолюбивый студент не аккуратен. Некоторые студенты аккуратны. Значит, некоторые студенты — не парни.

Исчисления традиционного типа

Исчисление — еще одно важнейшее понятие, наряду с формальным языком и семантикой введенное в число базовых математических конструкций математической логикой. ИсчислениеX опирается на некоторый формальный языкС и задает подкласс синтаксически правильно по­строенных объектов этого языка, порождаемых, или выводимых, вX . Для описания таких объектов и действий с ними используется новый класс синтаксических конструкций —выводы (часто называемые в конкретных исчисленияхпорождениями либодоказательствами). Выво­ды включают в себя формулы, термы либо другие объекты языкаС , организованные в систему таким образом, что каждый из них связан с ограниченным числом других согласно четким и проверяемым прави­лам, а глобальная структура вывода также подчинена четким и проверяемым условиям.

Пример 9.5.1. Исчисление, порождающее подстановки порядка п .

Выводимые объекты — векторы а вида { i \ , ¦ ¦ ¦ ,г п ), все г^ попарно различны и находятся в диапазоне 1 :п . Как известно, такие кортежи задают перестановки чисел 1,• • • ,и .

Выводы—циклические ориентированные графы с к пронумерованными вершинами, такие, что вершина i +1следует за i при i < к , первая следует за к-той, каждой вершине i сопоставлена подстановка O i , подстановка С в вершине, следующей за г , является произведением о\ и а^ . Например, следующий граф есть вывод в исчислении подстановок 4-го порядка:

Простейшим подклассом исчислений являются исчисления традиционного типа. Такое исчисление X задается описанием языкаС , акси­ом, являющихся выражениями языкаС , и правил вывода, каждое из которых имеет фиксированное конечное число посылок и одно заключение. Правила вывода обычно записываются в следующей форме:

Примененный здесь способ записи правил вывода является традиционным в математике. Над чертой стоят посылки, или аргументы, правила: формальные объекты, выведенные ранее, к которым разрешается применить правило. Под чертой стоит заключение, илирезультат: объект, который будет выведен после применения правила 4 . Рядом с правилом написано его имя (например,Zevs ). В соответствии с этим возникает следующее индуктивное определение выводимых (или порождаемых) объектов.

Определение 9.5.1. ЕслиЕ — аксиома, то S— выводимый объект.

Если Si , • • • , S n— выводимые объекты, Sполучается из них применением правила вывода, то S— выводимый объект.

Процесс порождения объекта согласно данному индуктивному определению представляется деревом, как доказано в § 6.1.

Определение 9.5.2. Вывод в исчислении I традиционного типа — конечное нагруженное дерево, листьям которого сопоставлены аксиомы, ребрам — положительные натуральные числа, остальным вершинам — пара из имени правила и объекта, получающегося применением данного правила к объектам, сопоставленным вершинам, непосредственно следующим за данной, взятым в порядке, соответствующем числам, приписанным ребрам, ведущим в эти вершины, причем количество вершин, непосредственно следующих за данной, равно количеству посылок в соответствующем правиле (обозначим его п), а ребра, в них ведущие, взаимно-однозначно занумерованы числами от 1 доп.

Таким образом, правила в исчислении, в отличие от правил в алгоритме или предложений в программе, лишь дают возможность совершить какие-то преобразования, но не обязывают нас сделать это. Как говорят, исчисление порождает объекты.

Пример 9.5.2. Рассмотрим исчисление для порождения палиндромов, или перевертышей (слов типа ‘кабак'), в алфавите А. Пусть ? — переменная, значениями которой являются буквы в алфавите А . Аксиомами являются пустое слово, обозначаемое (для того, чтобы его увидеть) А , и любая буква ? . Правило вывода единственное и с одной посылкой. менная, значениями которой являются буквы в алфавите А . Аксиомами являются пустое слово, обозначаемое (для того, чтобы его увидеть) А , и любая буква ? . Правило вывода единственное и с одной посылкой.

4 Удвоение терминов имеет здесь смысл для того, чтобы, с одной стороны, подчеркнуть сходство как с импликацией, так и с процедурой, и, с другой стороны, избегнуть путаницы при рассмотрении правил, относящихся, например, к импликации.

Вывод перевертыша ‘потоп' имеет вид (здесь последовательные применения правил мы не станем полностью разворачивать в дерево):

т

ото

потоп

Предложение 9.5.1. Объект S выводим в исчислении I тогда и только тогда, когда он встречается как корень в некотором дереве вывода.

Следствие теоремы 6.1.

На самом деле выводимым оказывается любой объект, встречающийся в некотором выводе. Таким образом, исчисления традиционного типа позволяют порождать и использовать лишь абсолютно правильные конструкции; если они имеют дело с формулами, то они не позволяют применять никаких гипотез, допущений и т. п. С точки зрения современной теории творческого мышления они формализуют полностью рутинный стиль мышления, когда человек не может даже допустить ничего, кроме того, что он считает истинным. Но с чисто математической точки зрения такое свойство традиционных исчислений часто полезно для доказательства точных результатов. Строго сформулировав исчисление, необходимо исследовать для него проблемы корректности и полноты. Корректность означает согласованность исчисления с семантикой выводимых объектов (в частности, для исчисления традиционного типа тождественную истинность всех доказуемых объектов). Корректность, безусловно, необходима для применения исчисления. Полнота означает возможность вывести любой семантически правильный объект в нашем исчислении. Полнота не является столь обязательным свойством, а зачастую и просто теоретически недостижима. Но уж если она возможна, иметь ее стоит.

Пример 9.5.3. Рассмотрим исчисление E равенств натуральных чисел, представленных в следующей форме: п как

п раз

SS ^~ S 0 .

Легко видеть, что это исчисление полно и корректно относительно обычной интерпретации равенств.

Пример 9.5.4. Немного изменим определение натурального числа из прошлого примера, отбросив 0. После этого, наряду с исчислением, получающимся из предыдущего заменой аксиомы на‘-, можно сформулировать исчисление Е\ , которое кажется более эффективным, добавив правило ?

n = m I =к

nl = тк

, умножение. Тем не менее можно доказать, что ни одно дерево вывода в расширенном исчислении не содержит меньше правил, чем в исходном .

Этот пример ставит важный и тонкий вопрос, связанный с представлением данных. Вывод представлен как дерево. Но дерево плохо тем, что его ветви абсолютно независимы, и получив однажды n = n , мы должны на другой ветви получать его вновь. Нельзя ли перейти к более эффективному представлению, не заставляющему копировать множество раз одни и те же куски вывода?

Таким представлением является сеть вывода . Ниже дана сеть вывода формулы 8 = 8, более короткая, чем соответствующее дерево.

SSSSSSSS = SSSSSSSS

vv

SSSS = SSSS

vv

SS = SS (9.14)

v S = S v

Сеть часто представляется в другом виде, более удобном для использования в математическом тексте. Это последовательность объектов. Каждый объект в этой последовательности является либо аксиомой, либо получается по одному из правил вывода из объектов, стоящих ранее. Известно, что при преобразовании сети в дерево количество объектов в выводе порою растет экспоненциально, т. е. пропорционально с • а п , гдеа > 1, и — количество объектов в выводе, с — константа.

Если исчисление содержит правила вывода, то возникает еще одно важное понятие.

Определение 9.5.3. Правило Пдопустимо в исчислении!, если множество выводимых объектов не изменяется после добавления П.

Например, правило Щ допустимо в исчислении ? из примера 9.5.3.

Упражнения к § 9.5

Что получится, если опустить требование конечности дерева в определении вывода?

Верно ли, что в рассмотренном выше исчислении для подстановок порядка k любая подстановка, встретившаяся в выводе, является выводимой?

Докажите, что в расширенном исчислении из примера 9.5.4 п=п выводится не менее чем за и применений правил.

Пусть задано исчисление традиционного типа, в котором языком является множество всех слов в алфавите { abc }, аксиомой — а, правилами вывода

XaY XaY Xe 66 Y XabY XcY XbbdY

Здесь X , Y — произвольные слова.

Вывести в этом исчислении ЪЪсЪ.

Построить граф выводимых слов не более чем из пяти букв; слова X , Y связаны ребром, если Y переводится правилом в X .

Привести пример слова, имеющего два существенно различных вывода.

Привести пример невыводимого слова

9.5.5. Пусть задано исчисление S традиционного типа, в котором языком является множество всех слов в алфавите {аЪ}, аксиомой —Ъ, правилами вывода

X X

аКа Ха

Показать, какие выражения выводимы в исчислении S .

Дать семантику, относительно которой данное исчисление было бы полным.

Показать, что правило

X6Y Y6Z X6Z

допустимо в исчислении S.

9.5.6. Рассмотрим теорию АА над языком слов в алфавите { S +=} с ак сиомой += и правилами вывода

X + Y =Z X + Y =Z

XS +Y = ZS X +YS = ZS

Вывести SS+SSS=SSSSS.

Доказать, что правило

X +Y = Z Y +X = Z

допустимо в исчислении АА.

3. Доказать, что АА полно и корректно для сложения натуральных чисел.

9.5.7. Рассмотрим исчисление в алфавите {()}. Аксиома: Л. Правила вывода:

(S) ! Е ! Ф

Охарактеризовать выводимые объекты.

Доказать полноту исчисления.

9.5.8. Видоизменим второе правило предыдущего исчисления на

S Ф

( НФ ) Чем это исчисление отличается от предыдущего? 9.5.9. Рассмотрим исчисление в языке выражений в алфавите

Qirbct ".

Аксиомы его

Правила вывода:

{ г , г , Ь , с } .

R — I P— D

Здесь ? — произвольное слово,Т — слово из букв t . Вывод — конечный граф, начальными вершинами которого являются акси­омы,Т в каждом применении правилаI отлично от использованных в остальных применениях этого правила, в каждом цикле применяется хотя бы одно правилоP . Выводимые объекты — встречающиеся в выводе.Т определено в выводе? , если оно является заключением правилаI .

Показать, что все Т , встречающиеся в любом выводе, определены.

Показать, что если сопоставить нашим выражениям типы Паскаля по принципу: г integer ;г > real ;Ъ > boolean ;с char ; (? i ...? та ) >> recorda l : end;

" >> " x ; (здесь T — идентификатора , определенный описаниемtype a = x ; x — тип, сопоставленный выражению? ,Гц — произвольные неповторяющиеся идентификаторы), то наше исчисление может рассматриваться как способ вывода корректных описаний типов языка Паскаль.

3. Показать, что, если убрать требование, чтобы в каждом цикле было правило P , наше исчисление становится некорректным.

Сформулировать полное и корректное исчисление для равенств постоянных выражений, составленных из натуральных чисел при помощи операций сложения.

Сформулировать полное и корректное исчисление для равенств постоянных выражений, составленных из натуральных чисел при помощи операций сложения и умножения.

Секвенции и формализация семантических таблиц

Для того, чтобы доказать корректность и полноту аппарата семантических таблиц для классической логики, необходимо прежде всего полностью формализовать этот термин, превратить его в математическую структуру.

Как обычно, точная формализация требует введения вспомогательных понятий, выявляющих многое из того, что скрыто за “общепонятными” словами в нестрогом описании. Важнейшее из них — секвенция. Прежде чем определить секвенцию, дадим неформальные пояснения.

Секвенция отображает некоторую стадию построения подтаблицы и состоит из всех результатов, полученных в ней в данный момент. Эти результаты, как мы уже видели, не просто формулы, а формулы с дополнительными спецификациями. Далее, при интерпретации секвенции необходимо учесть, что в некотором смысле метод семантических таблиц — метод доказательства от противного. Стремясь убедиться, что формула — тавтология, мы предполагаем, что она ложна, и старательно выискиваем все возможности, чтобы это нежелательное предположение оправдалось. Лишь неудача всех возможных попыток опровергнуть формулу заставляет нас принять, что она тождественно истинна. Данные соображения лежат в основе “парадоксального” определения истинности секвенции ниже.

Определение 9.6.1. Если задано множество спецификаций S , и a € S, а А — формула, то olA — специфицированная формула. Секвенция — набор специфицированных формул. Классическая секвенция — секвенция, где Sесть {|=, =| }, а формулы являются формулами логики предикатов.

Мы специально дали достаточно общее определение, поскольку секвенции используются и для неклассических логик. Большими греческими буквами Г ,А ,Л (возможно с индексами) будем обозначать произвольные (возможно пустые) наборы специфицированных формул. Аксиомы исчисления секвенций — секвенции вида Г ф {|=Л , =\ Л}. Вид­но, что аксиомы соответствуют закрывшимся подтаблицам, содержащим противоречия. Теперь правила для семантических таблиц могут быть переформулированы в правила исчисления секвенций. Нам достаточно показать технику переформулировок на примере правил для => и V .

I Г ф { 1=В }Г ф { =1А }| Г ф { =1В }ф {1= А }

1=^ Г ф {|= А ^ В } =1 ^ ГФНА ^ В }

1_ w Г ф {| =Ух А ( х ) } , у Г ф = |Ух А ( х )

Г ф {|=Ух А ( х )} ф {|=А ( а )} Г ф {|=A ( c n -\- i )} (9.15)

Правила для всеобщности требуют пояснения. Там, где берется старая константа, мы сохраняем |= Ух А{х) с тем, чтобы его можно было использовать и для других констант. Если же введена новая константа, мы уже выжали из квантора все, что возможно, и сохранять его смысла нет.

Исчисление секвенций — традиционного типа. Для нашего конкретного случая семантических таблиц (секвенций) нежелательные эффекты традиционного определения в значительной степени нейтрализуются тем, что нас интересует не столько вся секвенция как целое, сколько отдельные специфицированные формулы, входящие в нее. Еще одной приятной особенностью исчисления секвенций является то, что каждое правило вывода преобразует в результате лишь одну формулу; говорят, что оно применяется к этой формуле. Далее, формула, к которой применяется правило, собирается из своих подформул (возможно, с подставленными значениями свободных переменных). Таким образом, в дереве вывода в исчислении секвенций встречаются лишь подформулы формул, входящих в полученную секвенцию. Это свойство подформульности является чрезвычайно ценной особенностью секвенций и семантических таблиц, делающей их мощным инструментом в исследовании логических систем.

Исчисление секвенций создано немецким логиком Г. Генценом ( G . Gentzen ) в 1934 г. 5 Сам Генцен, и вслед за ним большинство логиков применяют другую систему обозначений: секвенция представляется как фигура Г — > А, где Г и А — наборы формул.

• 5 Его судьба была трагична. Он стал членом нацистской партии и ректором Пражского университета во время немецкой оккупации. За это он был расстрелян в 1945 г.

Г соответствует формулам, специфицированным как истинные, а А — как ложные. Пример дерева вывода в исчислении секвенций:

|= А , |=В , =\ А |=А , |=В , =\ В \ /

|= А , |=В , =\ ASzB

ж (9.16)

|= А , =\ ( В =>ASzB )

t =|А => ( В => АкВ )

В связи с локальной структурой дерева вывода появляется еще одно важное понятие. Если секвенция А находится в дереве выше секвенции Г, то для каждой из формул А имеется возможность однозначно определить подформулу одной из формул Г, в которую она переходит. Например, =| В из листа 2 переходит в подчеркнутую В в исходной =|А =>( В =>ASz B ). Дадим строгие определения.

Определение 9.6.2. Для правила |==> =|А в одном из аргументов и |=В в другом являются (непосредственными) результатами разбиения |=А =>В. Они соответствуют посылке и заключению этой импликации. Для правила =\ =>(непосредственными) результатами разбие­ния являются =\ В и\= А. Соответствие определяется аналогично. Для аргумента правила |= V |=A { ci ) — (непосредственный) результат, а |=Ух А ( х ) — результат разбиения |=УхА(х) в результирующей секвенции. Первый из них соответствует подформуле А ( ж ), второй—всей формуле. Для правила =\ У =\ А{с п +\) —(непосредственный)результат разбиения =\ Ух А{х) и соответствует подформуле А ( ж ). Для остальных правил результаты разбиения и соответствия для формул, к которым применяется правило, определяются аналогично. Для всех формул из Гони сами в аргументе являются результатами разбиения их же в заключении правила.

Если А есть результат разбиенияВ, В — результат разбиения С, то А есть результат разбиенияС и соответствует той подформуле С, которая соответствует в подформулеВ', соответствующейВ в С, подформулеА', соответствующейА в В 6 . Определим истинность и ложность

Часто результаты разбиения называют предками соответствующей формулы. Но эта секвенции в интерпретации.

Определение 9.6.3. Секвенция Аистинна в интерпретации ЭДТ, если хотя бы одна из ее формул противоречит своей спецификации; она ложна, если все формулы соответствуют своим спецификациям.

Таким образом, предполагая в начале построения семантической таблицы =| А, мы стремимся вывести секвенцию { =|А}, истинность которой означает истинностьА.

Теорема 9.1. (Теорема корректности для исчисления секвенций)

Если секвенция выводима, то она истинна в любой интерпретации.

Доказательство. Индукцией по числу секвенций в дереве вывода.

Базис. Пусть вывод состоит из одной секвенции. Тогда она является аксиомой. Значит, в ней есть формула, которая специфицирована и как истинная, и как ложная. Один из ее экземпляров и противоречит спецификации.

Шаг. Пусть корректность доказана для всех выводов с числом секвенций < и. Докажем ее для секвенций, выводимых за и шагов. Разберем случаи, когда результирующая секвенция получается по правилам для =4>и\/. Остальные рассматриваются аналогично. Пусть последним применялось правило =| =>, получена Г ф { =|А =>В } из Г ф { =|В } ф {|=А}. По предположению индукции, исходная секвенция истинна в любой интерпретации ШТ. Докажем более сильное, чем непосредственно требуется, утверждение: аргумент и результат правила одновременно истинны либо ложны в любой интерпретации 7 . Если аргумент ложен, то все формулы из Г удовлетворяют своей спецификации,В ложно,А истинна. По таблице истинности для =>, ложноА =>В. Обратно, если результат ложен, то все формулы из Г специфицированы правильно, и ложноА=? В. По таблице истинности, тогда истиннаА и ложноВ. Значит, и аргумент тоже ложен. Поскольку условия ложности аргумента и результата эквивалентны, эквивалентны и условия их истинности.

Для правила =| => установим эквивалентность истинности обоих аргументов и результата или, что эквивалентно, ложности хотя бы одного из аргументов и ложности результата. Если ложен результат правила, терминология зависит от точки зрения. Если рассматривать исчисление секвенций, то они скорее предки, а если рассматривать таблицы, они — потомки (конечно, измельчавшие).

• 7 Если бы у нас было возможно применять операцию ? к секвенциям, можно было бы сказать: секвенции в посылке и заключении эквивалентны.

То все формулы из Г специфицированы правильно, и истинно А =>В. По таблице истинности, тогда ложноА или истинноВ. Значит, хотя бы одна из посылок истинна. Наоборот, если ложен один из аргументов правила, то все формулы из Г специфицированы правильно, и лож­на посылка импликации либо истинно ее заключение. В любом из этих случаевА=? В истинна. Теперь рассмотрим правило |= V . Если ложен аргумент, то соответствуют своим спецификациям все формулы из результата, поскольку все они входили в аргумент. Если истинен результат, то он полностью входит в аргумент,а A ( ci ) истинно, поскольку истинноУх А ( х ).

И наконец, рассмотрим =| V . Здесь уже не выполнена эквивалентность истинности посылки и заключения в любой интерпретации. A ( cn + i ) может быть истинно в интерпретации ЭДТ, хотяУхА(х) ложно в ШТ. Но: из истинности аргумента влюбой интерпретации следует истинность результата влюбой интерпретации8.

В самом деле, возьмем произвольную интерпретацию ШТ сигнатуры секвенции Г ф { =| УхА ( х )}. В ней нет интерпретации для е та +ь поэтому ей соответствует целое семейство (ШТ а ) а6 и интерпретаций аргумента, отличающихся от ШТ лишь тем, чтос п +\ имеет значениеа € U . В каждой из ШТ а аргумент истинен по предположению индукции. Если для некоторого о€ U противоречит своей спецификации одна из формул Г, то поскольку она не содержитс п +\, она сохранит то же значение и в ШТ, и результат будет истинен. Если же ни для какогоа € U ни одной такой формулы из Г не найдется, то в любой ШТ а =|А{с п +\) противоречит своей спецификации, и, значит, A ( e re + i ) истинна при любом значении c n + i из U . По определению истинности, тогда в ШТ истиннаУхА(х), эта формула противоречит своей спецификации и результат истинен. ?

Итак, мы установили, что замкнутая семантическая таблица доказывает тождественную истинность проверяемой формулы. Более того,

Таким образом, данное утверждение имеет логическую форму

Vm 2 t ( m ) => VmQ 3( m ).

для логики высказываний преобразования при построении семантических таблиц оказываются эквивалентными.

Упражнения к § 9.6

• Определить правила исчисления секвенций для всех остальных связок классической логики.

• Перестроить в дерево секвенций семантические таблицы из предыдущих параграфов.

• Сравните число символов в таблице и в дереве секвенций. А число формул?

Семантические таблицы с равенством и для теорий

Исчисление предикатов с равенством характеризуется наличием выделенного двуместного предиката =, всегда интерпретируемого как совпадение, т. е. С (а =а ) = 1;С (а =6 ) = 0 для различающихсяа ,Ъ . Совпадение интерпретаций равных объектов гарантирует эквивалентность всех их свойств, согласно определению равенства, данному Лейбницем. Согласно теореме о замене эквивалентных, это означает, что Subst ( A ,х , t ) может быть заменено на Subst ( A ,ж , г), если |=t = г . Анализируя, где целесообразно проводить такую замену, видим, что она играет роль лишь там, где взаимодействуют две формулы, т. е. при выявлении противоречий, закрывающих подтаблицу Кроме того, необходимо учесть, чтоt = t всегда истинно. Это выражается следующими дополнительными правилами закрытия таблиц: если |=t = г либо |=г =t , то |= Subst ( A ,x , t ) и =| Subst ( A ,х , г ) составляют противоречие.=\ t = t есть противоречие само по себе.

Пример 9.7.1. Докажем утверждение У x i у {х = у => у = х).

=| УхУу ( х = у => у = х ) =|У у ( с = у =>у = с )

\= с = d =\ d = с =\ d = d

Семантические таблицы для равенства являются частным случаем семантических таблиц для теории. Пусть нам надо установить, являет­ся ли А теоремой Th . Тогда построим вывод секвенции |= Thф { =|А}.

Здесь |= Th означает совокупность всех аксиом Th , специфицированных как истинные. В семантической таблице это означает возможность в любой момент выписать формулу |= В, гдеВ ? Th . Поскольку аксиом может быть бесконечно много, нецелесообразно требовать обязательно выписывать их все в самом начале.

Правила для логики с равенством можно проинтерпретировать как применение теории со следующими аксиомами: обычная аксиома Ухх = х и две схемы аксиом

УхУу ( у = xSzSubst(A, z, х ) => Subst(A, z, у ));

\/ х \/ у ( х = ySzSubst ( A , z , х ) => Subst ( A ,z , у ));

где А — произвольная формула, не содержащая других свободных переменных, кромеz .

И наконец, рассмотрим случай, когда в сигнатуре теории присутствуют функции. Здесь действует очень простой закон. Выражения с, /( с ), /(/( с )), ... считаются различными, если в таблице не установлено равенство каких-либо из них, но ни одно из них не годится как новое, даже если оно еще никуда не подставлялось. Новой может быть лишь вспомогательная константа а. Когда появляется одна такая константа, то в таблице с функциональными символами она порождает бесконечно много выражений, которые требуется подставлять там, где правило использует старые объекты.

Упражнения к § 9.7

Проверить истинность следующих формул и рассуждений в логике с равенством и/или функциональными символами.

• Ух А ( х , f ( x )) => • Эх А ( х , х )

• Ух А ( х , /( ж ))& УхУу ( х = у ) => • Эх А ( х , х )

• ЭхУух = ySz Эх ( А ( х )&B ( x ))& Эх А ( х ) =>¦ ЭхВ ( х )

• Ух А ( х ) V Ух А ( х ) =>¦ ЭхУу ( х = у )

• Эх ЭуУг ( х = z V у = z ) Sz Эх ( В ( х )$? А ( х ))$? Эх ( В ( х )&А ( х )) =>¦ Уж В ( х )

• Ух Эу ( х = f ( y )) Sz Ух У у Уг ( х = yVx = zVy = z ) =>¦ y X f ( f ( x ))= x

• УхЗу ( х = /( у ))& Ух f { f { x )) = х => \/ ж УуУг ( х = у V х = z V у = z )

• \/ ж f ( f ( x )) = х => Ух Зг /( ж = f ( y ))

• \/ ж \/ г /( А ( ж )& А ( г /) => ж = г /)&­( а = 6) => Зж А ( ж )

• 9.7.10. УхУу { х = у =?¦ А { х ) V А ( у ))& Зж (. В ( ж )& А ( ж ))&\/ ж ( С ( ж ) => ­4( ж ))& ж ( С ( ж ) => Б ( ж )) => УхВ ( х )

В жизни рассуждения обычно представляют не полностью, опуская “очевидные из контекста” аксиомы либо факты, использованные в них. Такие рассуждения называются энтимемами. Проана­лизировать и пополнить следующие энтимемы. Корректность пополнения установить при помощи семантических таблиц.

Лисы умнее кур. Значит, ни одна курица не умнее лисицы.

Все тутси выше пигмеев. Значит, ни один пигмей не тутси.

Я боюсь зубных врачей. Я не желаю быть в одной компании с тем, кого боюсь. Значит, я не хочу быть в одной компании с вами.

Народы, у которых некоторые национальные герои — злодеи, воинственны. Народы, у которых некоторые национальные герои являются учеными, образованны. Аттила и фон Нейман — национальные герои Венгрии. Значит, венгры воинственны, но образованны.

Сделать выводы из посылок. Проверить их на таблицах.

Все курицы любят клевать пшено. Не все кошки жирные. Те, кто ест пшено, жиреет. Жирные не могут петь по ночам ...

Все козлята прыгают. Только здоровые молодые животные прыгают. Некоторые поросята не прыгают. На свете не более одного молодого существа, не являющегося козленком ...

Все павлины гордятся своим хвостом. Если кто-то гордится чем- то, не представляющим ценности, то он не может сделать ничего путного. Этот мост сделан павлинами. Все мосты в данной местности, кроме одного, — хорошего качества...

Те, кто любит учиться, не нуждаются в поощрениях. Для тех, кто не любит учиться, поощрение бесполезно. Следовательно... 9

Армия — школа жизни. Если жизнь бестолковая, то такова же и школа. Российская жизнь в данную пору — бестолковая. Только толковая армия может выиграть войну. Значит, ...

Чтобы проиграть войну, нужно проиграть хотя бы одно сражение. Наполеон в кампании 1812 г. выиграл все сражения. Эту кампанию он вел с Россией. Значит, ...10

Суворов во время итальянского похода выиграл все битвы и расстроил все планы противника. Если нет предательства, то расстроить планы противника достаточно для того, чтобы выигрыш битвы гарантировал победу в войне. Суворов проиграл Итальянскую кампанию. Значит, ...

(Н. Макиавелли) 11 Чтобы добиться успеха, политику необходимо выглядеть добродетельным. Кроме добродетельных и аморальных, никто не может выглядеть добродетельным. Если бы добивались успеха лишь аморальные политики, то никто не был бы добродетельным. Некоторые люди добродетельны...

9 Сделанный вывод явно софистичен. В чем обман?

Приведенные здесь исторические факты верны. Какая же посылка оказывается сомнительной?

Никколо Макиавелли — флорентийский общественный деятель и писатель. Он прославился своими книгами «Государь» и «Республика», в которых безжалостно показывал реальную, совершенно аморальную и бесчестную политику. Например, один из его принципов гласит, что пришедшему к власти в результате переворота правителю нужно опираться не на тех, кто поддержал его из идеи, а на тех, кто примкнул к нему ради выгоды, поскольку первые потребуют выполнения данных им обещаний.

Поскольку такой показ воспринимался как оправдание существующих гадостей, Макиавелли сам заслужил репутацию бесчестного человека, а неприличное поведение политиков до сих пор называют ‘макиавеллизм'. Сам Макиавелли в жизни был приличным человеком,ноего винавтом, чтоонставил личность ниже государства,что явилось корнем неисчислимых бед в истории.

Правда, стремление поставить личность выше государства приводило к не меньшим бедам, и уж во всяком случае к уничтожению народа либо цивилизации, пошедших по такому пути. Так что и здесь единственным выходом остается баланс.

Теорема полноты

Теорему полноты есть смысл доказывать не только для логики предикатов, но и для любой теории, базирующейся на классической логике, воспользовавшись сделанным в предыдущем параграфе обобщением семантических таблиц. Нам необходимо установить, что для каждой теоремы А теории Th найдется замкнутая семантическая таблица. Но здесь нужно было бы установить общий метод доказательства любой теоремы, а такового не существует, как будет доказано в разделе, посвященном теории алгоритмов. Поэтому придется действовать от противного: доказать, что незамкнутая семантическая таблица, удовлетворяющая некоторым критериям полноты, дает опровергающую модель дляА , т. е. модель Th , в которой ложноА . Далее установим, что начатую семантическую таблицу можно продолжить до полной. По контрапозиции отсюда следует, что полная семантическая таблица для любой теоремы закроется. Реализация изложенной схемы доказательства требует введения ряда важных вспомогательных понятий: полная таблица, незавершенная таблица...

Определение 9.8.1. Незавершенная семантическая таблица —дерево, каждой вершине которого сопоставлена секвенция, и секвенция в каждой вершине, не являющейся листом, получается из непосредственно следующих за ней по одному из правил вывода исчисления секвенций.

Таким образом, в незавершенной таблице снимаются требования конечности путей и того, что листьями могут быть лишь аксиомы. Содержательно говоря, незавершенная таблица является результатом нескольких разбиений, проделанных над интересующей нас формулой. Незавершенная таблица является одним из простейших примеров важного и для теории, и для приложений семейства понятий — незавершенных выводов.

Пример 9.8.1. Незавершенная таблица.

\- А , \- В , ЧASzB

t hА , Ч( В => •ASzB ) (9.17)

t ЧА => •( В => •ASzB )

Определение 9.8.2. Шаг разбиения — добавление правила тт и вершин над листом w незавершенной таблицы, не являющимся аксиомой, таким образом, чтобы w был получен по правилу тт из добавленных вершин.

Формула А пройдена в секвенции Г, если она присутствует либо в самой Г, либо в какой-нибудь секвенции на пути из корня незавершенной семантической таблицы в Г. Шаг разбиения избыточен, если хотя бы в одной из добавленных секвенций все непосредственные результаты разбиения пройдены в Г. Секвенция финальна, если она аксиома либо каждый шаг разбиения, применимый к ней, избыточен. Путь со не заперт, если он бесконечен либо заканчивается в финальной секвенции, не являющейся аксиомой.

Семантическая таблица полна, если все листья являются финальными секвенциями и для любого незапертого пути со в ней выполнены следующие три (для таблиц в теории — четыре) условия:

Если формула является конъюнкцией, импликацией, дизъюнкцией либо отрицанием, то в некоторой секвенции на пути встретятся все непосредственные результаты ее разбиения из одного из аргументов соответствующего правила.

Для любой встречающейся в некоторой секвенции пути со формулы вида =\ Ух А{х) ( |=Эх А ( х )) на со встретится формула вида =\ А ( ъ ) (|=А ( с г )).

Для любой константы а, входящей в некоторую формулу на со, и для любой встречающейся в некоторой секвенции со формулы вида |=УхА(х) (=\ ЗхА(х)) на со встретится формула \= A ( cj ) НА{а)).

(Для таблиц в теории Th) На со встречается |=А для любой А ? Th.

Лемма 9.8.1. (О построении контрпримера) В полной таблице по любому незапертому пути из корня можно построить интерпретацию, в которой истинны все встречающиеся на нем секвенции.

Доказательство. Доказательство леммы разбивается на две части: построение контрпримера и его верификация 12 .контрпримера. В качестве универса контрмодели M возьмем множество всех констант, встречающихся в секвенциях пути

• 12 В современном теоретическом программировании под верификацией понимаетсядо- казательство соответствия конструкции спецификациям, заданным при ее построении; здесь это означает истинность всех секвенций.

Каждая константа означает саму себя. ? ( P ( d ,..., с п )) есть _1_, если =|Р{с\, ...,с п ) встречается в какой-то секвенции насо; Т, если встречается |=Р{с\, ..., с п ). В остальных случаях оно определяется произ­вольным образом.

Верификация построения. То, что все секвенции путисо истинны, означает, что все встречающиеся в них формулы удовлетворяют своим спецификациям. Это утверждение доказывается индукцией по построению формулы.

Прежде всего элементарная формула, встретившаяся в некоторой се­квенции Ti на путисо, будет присутствовать и во всех последующих секвенциях, поскольку ни одно правило не может ее разбить. Поэтому на незамкнутом пути не встретится противоречащих друг другу элемен­тарных формул, и модель М определена корректно. Далее, по построению все элементарные формулы удовлетворяют своей спецификации. Базис индукции установлен.

Шаг индукции. Пусть соответствие спецификации уже доказано для всех формул с числом логических связок меньше и. ПустьА имеет и логических связок. Разберем случаи, соответствующие построению и спецификацииА.

Если рассматриваемая формула есть |= ( В => С), то, по определению полноты, на путисо найдется либо |= С, либо =|В. По предположению индукции, эти формулы удовлетворяют своим спецификациям. В каждом из этих случаев истинно( В => С). Если она есть =|( В => С), то по полноте на путисо встретятся и |=В, и =|С. Поскольку они удовлетворяют своим спецификациям,( В => С ) ложно.

Если формула имеет вид =| Ух А{х), то по условию полноты таблицы на путисо встретится =|A { ci ) для какого-тоа, иУх А{х) ложно.

Если формула есть |= Ух А{х), то по полноте насо встретится |=A ( ci ) для любой константыа, принадлежащей универсу контрмоделиМ. По предположению индукции, любая из =|A { ci ) удовлетворяет сво­ей спецификации и, значит, истинна. Но тогда по определению истинности истинно иУх А{х).

Остальные связки разбираются аналогично.

Осталось убедиться, что полную таблицу всегда можно построить. Для этой цели сформулируем стратегию корректного разбиения формул, приводящую к такой таблице. Стратегия не будет определять однозначно, какая формула должна быть разбита в данный момент. Она лишь ограничивает допустимые разбиения.

Занумеруем все константы из сигнатуры теории нечетными натуральными числами. Все вспомогательные константы занумеруем четными. Занумеруем все аксиомы теории. Введем дополнительные специ­фикации для аксиом теории и многократно используемых (МИ) формул вида |= Ух А ( х ) и =|Эх А ( х ). Аксиома может быть разрешена или за­держана. Каждой МИ-формуле сопоставим множествоа констант, по которым она уже разбивалась; кроме того, она может быть временно запрещена. Формула временно запрещается, когда происходит ее разби­ение. Корректное разбиение МИ-формулы может производиться лишь по константеа € а , при этома добавляется ка . Корректное разбиение не может производиться по временно запрещенной или задержан­ной формуле. Секвенция условно финальна, если в ней не может быть произведено ни одного неизбыточного корректного разбиения.

Стратегия корректного разбиения. Вначале задерживаем все аксиомы, кроме первой, и не запрещаем ни одной МИ-формулы. Пока формула не является условно финальной, производятся лишь корректные разбиения, причем разбиение МИ-формулы производится по константеCi , имеющей минимальный номер среди всех таких констант, встреча­ющихся в незадержанных формулах секвенции. Когда секвенция оказалась условно финальной, разрешаем первую из задержанных аксиом и снимаем все временные запрещения.

Лемма 9.8.2. В незавершенной семантической таблице для теории в любой секвенции число формул, не являющихся результатами разбиения аксиом, конечно.

Доказательство. В корне дерева такая формула всего одна. Каждый шаг разбиения увеличивает их количество не более чем на 1.?

Лемма 9.8.3. (Лемма о корректных разбиениях) Любая последовательность корректных разбиений над секвенцией, содержащей конечное число разрешенных аксиом, за конечное число шагов приводит к условно финальной.

Доказательство. Определим ранг секвенции как количество логических связок в формулах, не являющихся задержанными либо временно запрещенными. В условиях леммы ранг конечен, поскольку число таких формул конечно. При каждом разбиении ранг уменьшается на 1.?

Следствие. На любом бесконечном пути в таблице, построенной согласно стратегии корректных разбиений, имеется бесконечно много условно финальных секвенций.

Докажем теперь, что для каждой МИ-формулы А , встретившейся в секвенцииГ на незамкнутом путисо , на этом пути встречаются результаты ее разбиения по каждой константеа , встречающейся насо . Еслисо завершается финальной секвенцией, то любое разбиениеА избыточно и, соответственно, любое разбиение по любой константеа пройдено в финальной секвенции. Если же путьсо бесконечен, то в промежутке междуг -той и( г + 1)- ой условно финальными секвенциями, встретившимися насо после появленияА иа , А будет разбито поа .

Для любой обычной формулы результаты ее разбиения встретятся на со до следующей условно финальной секвенции после того, как она появилась либо стала разрешена (если формула является аксиомой).

Итак, любая таблица, построенная в соответствии со стратегией кор ректных разбиений, полна. ?

Таким образом, если полная таблица не является выводом в исчислении секвенций, то она дает модель, в которой все аксиомы Th истинны, а проверяемая формула А ложна. Комбинируя доказанное утверждение с теоремой корректности, получаем:

Теорема 9.2. ( Теорема полноты классической логики) ThЬ А тогда и только тогда, когда существует вывод секвенции |= Thф {=|А}.

Таким образом, синтаксическая доказуемость при помощи семантических таблиц совпадает с семантическим отношением логического следования. Теорема полноты (в формулировке, связанной с другой формализацией логики) была первым фундаментальным результатом математической логики, доказанным в 1930 г. великим логиком XX века К. Гёделем (К. Godel ) 13 . Теорема полноты влечет несколько важных следствий.

Определение 9.8.3. Thсинтаксически непротиворечива, если не замы­кается семантическая таблица ни для какой формулы вида A &A .

На самом деле теорему полноты (в форме теоремы существования модели) предвос­хитил, но не сумел понятно сформулировать и доказать Лёвенгейм ( L . Lowenheim ) еще в 1915 г. Его работа осталась незамеченной и была заново открыта лишь после доказательства Гёделя.

Следствие 1. (Теорема существования модели) Если Th синтаксически непротиворечива, то она имеет модель.

Незапертый путь в полной таблице для |= Th Ф {=| A &A\ дает искомую модель.

Следствие 2. (Теорема компактности) Если Th ЬA, то найдется конечная подтеория Tho С Th , такая, что Tho ЬA.

В самом деле, найдется замкнутая семантическая таблица для A. Она использует лишь конечное число аксиом Th .

Следствие 3. (Теорема компактности, форма 2) Если любая ко­нечная подтеория Th непротиворечива, то Th непротиворечива.

Доказательство. Действуем от противного. Если семантическая таблица для |=Th U { =|A &A } замкнута, то найдется конечная Tho С Th , такая, что Tho противоречива. Значит, если теория противоречива, то противоречива некоторая ее конечная подтеория. По контрапозиции, получаем отсюда искомую форму теоремы компактности. ?

Следствие 4. (Теорема компактности, форма 3) Если любая ко­нечная подтеория Th имеет модель, то и Th имеет модель.

Комбинация следствия 3 и теоремы существования модели.

Следствие 5. (Теорема о взаимной противоречивости) Если те­ории Thi и Tli 2 непротиворечивы, а теория Thi U Th 2 противоречива, то найдется конечное число аксиом Thi и конечное число аксиом ТИг, которые противоречат друг другу.

Следствие 6. (Теорема о взаимной непротиворечивости) Если теории Thi и Th 2 непротиворечивы и любое конечное число аксиом Tli 2 не противоречит Thi , то теория Thi U Th 2 непротиворечива.

Доказательства этих следствий являются экзаменационными дополнительными вопросами на оценки 4-5.

Вы видите, сколько разнообразных форм, внешне совершенно не похожих друг на друга, может быть выведено как непосредственные следствия фундаментальной теоремы. Таким свойством обладают все принципиальные математические результаты. Но отнюдь не всегда их следствия становятся ясны сразу после их открытия. На первый взгляд (скажем) теорема компактности выглядит как тривиальное следствие теоремы полноты. Но потребовалось около двух десятилетий для формулировки теоремы компактности после того, как была полностью осознана формулировка теоремы полноты, да и первые ее доказательства были не такими простыми. Более совершенный аппарат позволяет ярче выделить взаимосвязи. Интересна и ее история. Она была доказана русским логиком А. И. Мальцевым во время II мировой войны и опубликована в Вестнике Ивановского педагогического института. Естественно, что публикация осталась незамеченной, и десятью годами позже она была “переоткрыта” Л. Хенкиным. Правда, историческую справедливость удалось восстановить, но теперь кое-кто утверждает, что она практиче­ски содержалась в уже упомянутой работе Лёвенгейма.

Упражнения к § 9.8

Доказать, что любая модель теории Th с равенством может быть преобразована в такую, в которой равенство определяется как совпадение.

Доказать, что теория без равенства, имеющая модель с и элементами, имеет и модель си + 1 элементом.

Доказать, что теория с равенством, у которой есть модели со сколь угодно большим числом элементов, имеет модель с бесконечным числом элементов.

Студент Гениалькис доказал, что все счетные модели теории с равенством R , описывающей порядок и его взаимоотношения со сложением и вычитанием на множестве рациональных чисел и имеющей перечисленные ниже аксиомы, изоморфны:

Ух X < х УхУуУг ( х < ySzy < z =>¦х < z )

Ух 0 +х =х Ух Зу 3 z ( y < x & x < z )

Ух х + 0 =х Ух Уу ( х < у => •3 z ( x < zSzz < у ))

Ух х +( —х ) = 0Ух УуУгх + ( у + г ) = ( х +у ) +z

1 > 0 Ух У у х +у = у +х

Ух У у V' z ( x +у = х +z =>у = z )

Ух Уу ( х > 0 =>х + у > х )

Доказательство занимает 121 страницу. Будете ли Вы его читать; если нет, то почему?

Известно, что если из предыдущей теории выбросить сложение, то все ее счетные модели действительно будут изоморфны. Как же согласовать это с существованием нестандартных моделей?

Какая аксиома теории R лишняя (следует из остальных)?

Сечения

Еще одним важным следствием теоремы полноты для семантических таблиц является теорема об устранении сечений.

Теорема об устранении сечений. Если семантические таблицы дляГ ф { =|А } иГ ф {|=А } закрываются, то закрывается и семантическая таблица дляГ .

Доказательство. Поскольку в любой интерпретацииА либо истинно, либо ложно, в соответствующей секвенции противоречит (по теореме корректности) своей спецификации одна из формулГ . Значит,Г тождественно истинна и по теореме полноты имеет замкнутую семантическую таблицу.?

Правило сечения

Г ф { = |А } Г ф {| =А } Г

присутствовало в исходной генценовской формулировке исчисления секвенций, и доказательство устранимости сечений было первым серьезным результатом его работ. Формула А называетсяформулой сечения либо формулой, по которой производится сечение.

Заметим, что наше доказательство, хотя и краткое, обладает одним существенным недостатком, которого лишено гораздо более длинное доказательство Генцена. Оно полностью неконструктивно, не дает никакого способа преобразования замкнутых таблиц для его посылок в таблицу для заключения, кроме тривиального указания “ищите и обрящете”. Логический статус приведенного доказательства полностью аналогичен логическому статусу следующего доказательства того, что в шахматах, правила которых видоизменены таким образом, что каждая сторона делает два хода подряд, белые проиграть не могут.

В детерминированной конечной игре обязательно имеется либо стратегия, ведущая к выигрышу одной из сторон, либо стратегия, ведущая к ничьей 14 .

14 Кажется, что оговорка о конечности здесь перестраховка, но предположение о существовании выигрышной стратегии у одного из игроков для бесконечных игр оказалось новой аксиомой теории множеств, альтернативной аксиоме выбора (т. е.несовместимой с ней, но вроде бы не противоречащей всем остальным аксиомам)!

Рассмотрим три возможных случая. Если стратегия ведет к выигрышу белых либо к ничьей, то все доказано. Пусть она ведетк выигрышу черных. Тогда, воспользовавшись тем, что есть фигура, которая может ходить в начальной позиции (а именно, прыгающий черездругие фигуры конь),сделаем ею ход, а затем вернем ее на исходную позицию (например, 1. Kg 1– f 3, Kf 3– g 1). Тогда мы передадим ход черным, и по предположению они теперь должны проиграть, что абсурдно. Итак, третий случай исключается.

Тот, кто попытается в реальной игре походить два раза конем туда- обратно, скорее всего проиграет, так что никакого способа достичь хотя бы ничьей это доказательство не дает.

Устранение сечений внешне похоже на разбор случаев A ? A , но отнюдь не сводится к нему. Оно имеет место и для многих неклассических логик, в которых закон исключенного третьего отсутствует. Оно проваливается в ряде систем, в которых закон исключенного третьего есть.

Ввиду исключительной важности данного правила мы рассмотрим и синтаксическое доказательство устранимости сечений, дающее способ перестройки таблицы без сечений в таблицу с сечениями. Более того, мы покажем, что имеется совокупность преобразований замкнутых таблиц, устраняющая из них сечения, и такая, что процесс устранения заканчивается независимо от порядка применения данных преобразований. Эти преобразования называются шагами нормализации таблицы. Шаги нормализации определяются в соответствии с главной связкой формулы сечения и с тем, созданы ли обе формулы сечения в посылках непосредственно на предыдущем шагу или же хоть одна из них передается от предыдущих секвенций без изменения.

Перед тем как их определить, докажем возможность некоторых преобразований выводов в исчислении секвенций, а именно: ослабления секвенций путем дописывания новых членов, подстановки конкретного значения вместо вспомогательной константы в заключении, т. н.обра­щения всех правил исчисления секвенций15 и сокращения нескольких экземпляров одинаковых формул в заключении вывода. Далее покажем, что эти преобразования не усложняют вывода, но при этом несколько модифицируем понятие вывода. Аксиомами теперь будут лишь противоречия из элементарных формул. Очевидно, что любое противоречие из пары сложных формул разбивается на элементарные, так что с теоретической точки зрения понятие выводимости не изменяется 16 . модифицируем понятие вывода. Аксиомами теперь будут лишь противоречия из элементарных формул. Очевидно, что любое противоречие из пары сложных формул разбивается на элементарные, так что с теоретической точки зрения понятие выводимости не изменяется 16 .

• 15 На самом деле мы уже указали на возможность обращения правил, разрешив пользоваться для сокращения семантической таблицы обратными преобразованиями.

Предложение 9.9.1. (Подстановка) Вывод секвенции Г ф{ А ( с п + \)}, где с п +\ не входит в Г, без увеличения числа применений правил и сложности встречающихся формул перестраивается в вывод Г ф{ А ( х \ t )} для произвольного терма t .

Доказательство. Начнем с частного случая подстановки — переименования вспомогательной константы. Докажем, что если q не входит в формулы из Г, то вывод Г [ ж | c n + i ] можно преобразовать в вывод Г [ ж |сЦ. В самом деле, противоречия после такой замены останутся противоречиями, и мы получаем базис индукции по длине вывода. Далее, все применения правил после такой замены остаются корректными применениями правил, кроме, может быть, двух правил, использующих17 вспомогательную константу, да и то в случае, когда эта константа совпадает сс\. Рассмотрим одно из них, например,

?

Г ф {| = А ( с {) }

Т ' ф {^ ЗуА ( у )}

Здесь, как и ниже в описаниях преобразований, ? обозначает вывод стоящей ниже его секвенции. В ? меньше применений правил, чем в исходном выводе, Г' не содержит с;. Поэтому по предположению индукции i можно переименовать везде внутри ?, например, заменив ее на д., не входящее в ? и не совпадающее с e re + i . После чегох можно повсюду заменять нас;.

Теперь проведем подстановку терма. Все константы, входящие в t и не входящие в Г, переименуем. После такого переименования все применения правил после подстановки останутся корректными. ?

Результат применения преобразования подстановки к выводу ? обозначаем, аналогично подстановке в формулу, ? [ e n + i | t ]. Проведенное ментарных компонент уже встретив ееся противоречие доказательство подчеркивает аналогию связанных переменных в формуле и вспомогательных констант в выводе: на самом деле мы занимались именно устранением коллизий.

• 16 Конечно, с практической точки зрения может быть утомительно разбивать до эле- нтарных компонент уже встрети

В терминах таблиц: вводящих.

Предложение 9.9.2. (Ослабление) Вывод секвенции Гперестраивается без увеличения числа применяемых правил и сложности формул в вывод секвенции Г ф А.

Доказательство. Сначала при помощи подстановки переименуем внутри вывода Г все вспомогательные константы, входящие в А и не встречающиеся в Г. Затем просто дописываем А ко всем секвенциям в исходном выводе. ?

Предложение 9.9.3. Вывод заключения любого из правил исчисления секвенций перестраивается в вывод любой из своих посылок без увеличе­ния числа применяемых правил и сложности формул.

Доказательство. Ведется индукцией по числу применений правил в выводе исходной секвенции.

Если примененных правил вообще нет, то исходная секвенция — аксиома, а поскольку противоречие состоит из элементарных формул, оно находится в Г, и результирующая секвенция также является аксиомой.

Пусть теперь обратимость доказана для всех выводов с числом правил не более и. Докажем для выводов с и + 1 правилом.

Проанализируем правила обращения для конъюнкции и всеобщности (остальные правила рассматриваются совершенно аналогично).

Докажем, что вывод Гф {|= А &В } без усложнения перестраивается в вывод Г ф {|=А , |=В}. Проанализируем последнее из примененных в выводе правил. Если это правило создало |=А &В, то просто отбрасываем его, если же оно его не затрагивало, то обращаем по предположению индукции выводы-посылки данного правила. Так же поступаем в случае =|А &В, но здесь в случае, если последним применялось правило =| &, отбрасываем целое поддерево вывода, поскольку нас интересует лишь одна из его посылок.

Рассмотрим перестройку вывода секвенции Г ф { =| Ух А ( х )} в вывод секвенции Г ф {=|А{с п +\)}. Опять-таки если последнее правило создало =|Ух А{х), то отбрасываем его, иначе обращаем вывод посылки. Для истинности рассуждение совершенно аналогично. ?

Предложение 9.9.4. Вывод секвенции Г ф {|=А , \= А } без увеличения числа применений правил и сложности встречающихся формул перестраивается в вывод Г ф {|=А}. Аналогично для = \ А .

Доказательство. Ведется индукцией по числу применений правил в выводе исходной секвенции.

Если она является аксиомой, то после устранения отдублированной формулы она аксиомой и останется.

Если последним применялось правило, не затрагивающее ни одного из экземпляров сокращаемой формулы, то по предположению индукции можно применить сокращение к выводам посылок и по тому же правилу получить вывод сокращенного заключения.

Если последним применялось правило к сокращаемой формуле, то рассмотрим ее вид. Пусть она имеет вид В к С . Тогда вывод выглядит следующим образом

? Г ф {|=В к С , |=В , |=С }Г ф {|=В к С , |=В к С }

Тогда по обратимости можно перестроить вывод ? без увеличения длины в вывод?' , дающий секвенцию

Г ф {|=В , |=С , |=В , |= С }.

А теперь, применив сокращение, получаем из него вывод

?" Г ф {|=В , |=С , |=С }

Длина ?" не больше длины? , и опять можно применить предположение индукции, сократив еще раз:

Е"'

Гф {|= В ,|= С }

А теперь возвращаем на место последнее правило:

Е"'

Г ф {|=В , |=С }Г ф {|=В к С

Рассмотрим случай В VС'. Тогда вывод имеет формуSi ? 2

г © {| =в v с , | =. в }г © {| =в v с , | =с }г ф {|=в v с , |=в v с }

Отсюда обращениями получаем

?' ?'

Гф {|= В ,|= В } Гф {|= С ,|= С }

Применяем имеющиеся по предположению индукции сокращения и возвращаем на место исходное правило:

Г ф {| = В } Г ф {| = С }

г ф {|=в v с }

Есть еще одно место в исчислении секвенций, где возникают трудности при нормализации. Кванторы =| 3 и |= V “бессмертны”: они не ис­чезают и дотягиваются из результата до всех аксиом-противоречий. Как Вы видели, действительно часто их нужно использовать многократно, но не бесконечное же число раз!18 Поэтому желательно было бы кое- когда от них избавляться.

Предложение 9.9.5. (Удаление последнего квантора) Если вывод имеет вид

?

Г ф { = | А [ х \ t ], =\ Эх А ( х ) У

ГфН ЭхА ( х )}

и внутри ?формула =\ Эх А{х) более нигде не разбивается, то без уве­личения длины вывода и сложности формул можно преобразовать ?в вывод Г ф { =|А [ х | ?]}. Аналогично для |= V.

Определим шаги нормализации.

Шаг 0. Если главная связка формулы сечения является пропозици­ональной и она не разбивается хотя бы в одной из его посылок, либо ее

Это нужно лишь для опровержения, но не для доказательства.

главная связка — квантор и ни в одной из посылок для него не вводится вспомогательная константа, то выполняем одно из следующих преобразований подъема сечения в зависимости от того, какое правило применялось к одной из секвенций-посылок (эта секвенция для формул с пропозициональной связкой может выбираться произвольно, а для кванторных — соответствует посылке видаГ ф {|=Зх А ( х )} либоГ ф НУхА ( х )}).

Si Г ф {| =А , = \ В , = \ С } ? 2

Г ф { =|А => В , |=С } Г ф { =|А => В , =|С }

Г ф {=|А => В }

Si ? 2

Г ф { =А , = В }

Г ф {|=А , = \ В , = \ С }Г ф {|=А , = \ В , |=С }

Г ф {=|А => В } Для двухпосылочного правила:

Г Ф { = |А , | =С }Г ф {| =В , | =С }? 5

Г ф {|=А => В , |=С }Г ф {|=А => В , =|С }

Г ф {|=А => . В }

? 4S 5

Г ф {|=В , |=С }Г ф {|=В , = \ С }

^ 3Sg

Г ф { = |А , | =С }Г ф { = |А , = |С }

р 0 г _ |_ д \ Г ф {| =. В }

Г ф {|=А => • В }

?' 2 получается обращением ?2,^' 5 ,?' 5' — два обращения? 5-

Для остальных пропозициональных связок преобразование произ­водится аналогично

Рассмотрим теперь кванторы.

Si Г ф { = |Эх А ( х ), =\ А ( х |t ), | = С } Ег

Г ф { =| Зх А ( х ) , |= С } Гф {=|Эх А ( х ), =\ С }

Г ф {=| Эх А ( х ) У

Si S 2

Г ф {=| Зх А ( х ), =\ А ( х |t ), \= С } Г ф {=|Зх А ( х ), =\ А ( х \ t ), =\ С }

Г ф { = | Эх А ( х ), =\ А ( х | i ) } Гф { Ц ЗжА ( ж )}

Для вспомогательной константы:

S3 Г ф {|= A ( c n + i ), |=С } S 4

Г ф {|= Зх А ( х ), |= С } Г ф {|= ЗжА ( х ), =\ С }

Г ф {|= Эх А ( х ) У

S 3S 4

Г ф {|= А ( сп -\-\), |= С } Г ф {|=А ( сп -\-\), =\ С }

Гф {

Гф {

А ( с п +1 ) }

ЗхА ( х )}

S 2 , S ^ получаются обращениями соответствующих выводов.

Для квантора V преобразования аналогичны.

Шаг 1. Если одна из посылок правила сечения является аксиомой, то рассматриваем следующие два подслучая.

Формула сечения не участвует в противоречии. Тогда и в результате правила сечения имеется то же противоречие и, следовательно, результат является аксиомой. Значит, правило сечения вместе с его посылками и всем, что лежит над ними, можно просто опустить.

Формула сечения участвует в противоречии. Здесь опять придется разобрать два подслучая, но они совершенно симметричны.

(а) Пусть противоречием является левая посылка. Тогда она имеет вид Г ф {=| А , |=А },

а правая, соответственно, Г ф {=|А , =\ А }.

Заключение сечения имеет вид Гф{ =| А}. Значит, его можно получить из правой посылки преобразованием сокращения (предложение 9.9.4), не увеличивая длины вывода и сложности формул.

(б) Симметрично. Связка . Для отрицания

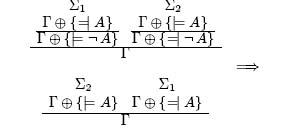
Связка V . Для кванторов

Здесь в выводе ? выделены все применения правила |= V к формуле сечения. Sj — выводы посылок таких правил, в которых имеются другие применения тех же правил, S j — выводы, в которых других применений |= V к формуле сечения нет. ?' получается из Sj устранением последнего применения кванторного правила по предложению 9.9.5, аЩ — вычеркиванием всех формул |=Ух А{х).

Связка =>. Пусть главная логическая связка формулы сечения — импликация и в обоих посылках сечения она разбирается. Тогда имеем следующее преобразование:

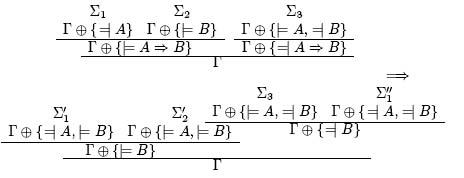
Выводы со штрихами — ослабления соответствующих исходных выводов.

Связки &, V . Для остальных бинарных пропозициональных связок преобразование определяется аналогично.

Из всех шагов нормализации обоснования требуют лишь квантор- ные. Достаточно заметить, что после устранения первых применений кванторного правила последующие за ними также становятся первыми, и т. п. Это легко оформляется индукцией.

Теорема 9.3. (Сильная теорема нормализации) Любая последователь­ность шагов нормализации за конечное число шагов приводит к выводу без сечений.

Доказательство. Для обоснования этого достаточно приписать любому сечению высоту, которая будет уменьшаться на каждом шаге нормализации и оценивается в единицах, множество которых удовлетворяет свойству бесконечного спуска. Натуральными числами оценить не получается из-за того, что слишком часто при нормализации одно сечение заменяется на несколько; приходится оценивать ординалами. А изобретение такой оценки можно рассматривать как задачу на ‘отлично' для студента (подсказка: удобнее всего воспользоваться сложением по Куратовскому и возведением в степень).

Упражнения к § 9.9

(Для тех, кто хорошо знает официальные правила шахмат и играл в турнирах) Приведенное в примечании на стр. 254 доказательство ошибочно. Найдите неточность и исправьте ее19.

В японских шахматах ничьей нет. Тот, кто сделал ход, ведущий к троекратному повторению позиции, считается проигравшим. Ко­ролю не запрещено ходить под шах, так что при возникновении ситуации, которая в европейских шахматах считалась бы патом, король обязан пойти под бой и пасть смертью храбрых20. В начальной позиции многие фигуры 21 могут походить и затем вернуться назад. Можно ли перенести наше доказательство на модифицированные японские шахматы? А может быть, Вы придумаете для них другое?

Если не отказываться от неэлементарных противоречий, какой из пунктов доказательства теоремы об устранении сечений провали­вается? Как можно было бы спасти его, изменив меру сложности вывода?

Студент Гениалькис принес Вам доказательство того, что каждый вывод секвенции Г ф {=|Эх А ( х )} можно перестроить в вывод секвенцииГ ф {=|А ( х |t \), ...,=(А ( х |t n )} для некоторыхti , ... , t n , не увеличивая число шагов в выводе, но Вы тетрадь с доказательством потеряли. Как Вы ответите на вопрос Гениальки- са, верно ли его доказательство? 22

Ошибка возникает лишь при взаимодействии с полной системой правил шахматной игры в официальных соревнованиях.

На самом деле там такая ситуация может возникнуть лишь теоретически, поскольку взятые фигуры (кроме, естественно, короля) переходят на сторону противника и воюют против бывших своих. Но это уже не имеет отношения к математическому содержанию задачи.

Правда, на сей раз кроме коня, поскольку пешки стоят в третьем ряду, а конь ходит только вперед. Но это также не имеет отношения к задаче.

Поскольку студент гениальный, все доказательства верных теорем, которые он дает, правильны, а поскольку человеку свойственно ошибаться

26. Отношения между сложными суждениями. Понятие логического следования

Отношения между сложными суждениями те же самые, что и между простыми, она также могут быть сравнимыми и несравнимыми, а сравнимые могут быть совместимыми и несовместимыми. Соответственно, отношения между совместимыми сложными суждениями те же: эквивалентность, подчинение, частичная совместимость (субконтрарность). А между несовместимыми: противоположность и противоречие.

Несравнимые сложные суждения – это суждения, которые не имеют общих пропозициональных переменных (простых суждений). Например, суждения «p V q» и «a & b» являются несравнимыми.

Сравнимые суждения – это суждения, имеющие одинаковые пропозициональные переменные (простые суждения) и отличающиеся логическими связками, включая отрицание. Например, «Либо Москва, либо Одесса являются морским портом», или в символической форме: «p V q» и «Москва не является морским портом, а Одесса является морским портом», или: « p & q».

Мы не будем полностью рассматривать отношения между сложными суждениями, а лишь некоторые из них.

Начнем с эквивалентности. Как мы помним, эквивалентные суждения – это такие, которые принимают одни и те же значения, т.е. являются одновременно истинными или одновременно ложными.

Отношение эквивалентности интересно тем, что оно позволяет выражать одни сложные суждения через другие, например, конъюнкцию через дизъюнкцию, импликацию через дизъюнкции и т.д., и получать в итоге так называемые законы логики.

Приведем четыре известные эквивалентности (законы логики):

1. Выражение конъюнкции через дизъюнкцию:

(a Λ b) ≡  a V  b

2. Выражение дизъюнкции через конъюнкцию:

(a V b) ≡  a Λ  b

Эти две эквивалентности называются законами де Моргана.

3. Выражение импликации через конъюнкцию:

(a → b) ≡ (a Λ  b)

4. Выражение импликации через дизъюнкцию:

a → b ≡  a V b

Отношения между сложными суждения записываются с помощью тех же таблиц истинности, но несколько иначе. Например, отношения эквивалентности выглядят так:

А ≡ В

и и и лл и л л

1-я и 4-я строки таблицы показывают, что суждения А и В одновременно принимают одинаковые значения; а перечеркнутые строки 2 и 3 говорят о том, что эквивалентные суждения не могут принимать различные значения.

Если мы вспомним, что частично совместимые суждения могут быть одновременно истинными, но не могут быть одновременно ложными, то таблица примет такой вид:

А V В

и и и л л и л л

Подчинение имеет место тогда, когда при истинности подчиняющего подчиненное тоже истинно. Для подчинения таблица будет выглядеть так:

А → В

и и и л л и л л

Отношение логического подчинения, позволяющее по истинности подчиняющего суждения определить истинность подчиненного составляет основу фундаментального для науки логики понятия логического следования, которое регулирует все виды рассуждений.

Что касается несовместимых суждений, то надо вспомнить, что такие суждения не могут быть одновременно истинными. Совместимость имеет те же два вида – противоположность и противоречие.

Противоположность – отношение между суждениями, которые могут быть одновременно ложными, но не могут быть одновременно истинными. В табличной форме противоположность выглядит так:

А Λ В

и и и л л и л л

Противоречие – отношение между суждениями, которые не могут быть одновременно ни истинными, ни ложными:

А  В

и и и л л и л л

Чтобы получить сложное суждение, противоречащее исходному, исходное суждение надо подвергнуть отрицанию, например, для р противоречащим будет  р, а для p V q, соответственно,  (p V q).

В заключение следует сказать, что отчетливое представление об отношениях, в которых могут находиться суждения, позволяет логически грамотно анализировать высказывания участников дискуссий. Бывают ситуации, когда логический анализ показывает совместимость различных по структуре суждений. Нередко это случается с частными суждениями. Пропонент утверждает, что «Некоторые S есть Р», а оппонент настаивает, что «Некоторые S не есть P». На поверку же выходит, что эти суждения не исключают друг друга, а являются частично совместимыми (субконтрарными) и оба могут оказаться истинными.

ВЫВОДЫ по 2 вопросу:

1. Суждения, как и понятия, делятся на сравнимые (имеют общий субъект и предикат) и несравнимые.

2. Сравнимые суждения делятся на совместимые и несовместимые. Суждения совместимы, если они могут быть одновременно истинны, т.е. если они выражают одну и ту же мысль полностью или лишь в некоторой части. Отношения совместимости бывают трех видов: эквивалентность, подчинение и субконтрарность.

3. Суждения несовместимы, если они не могут одновременно быть истинными. Они делятся на два вида: отношения противоположности (контрарности) и противоречия (контрадикторности).

4. Отношения между суждениями типа А, I, E, О изображают с помощью логического квадрата.

5. Отношения между сложными суждениями аналогичны отношениям между простыми суждениями.

27. Законы логики и логические противоречия

Закон противоречия. Законы логики

В логике, как и во всякой науке, главное – законы. Логических законов бесконечно много, и в этом ее отличие от большинства других наук. Однородные законы объединяются в логические системы, которые тоже обычно именуются логиками.

Без логического закона нельзя понять, что такое логическое следование и что такое доказательство. Правильное, или, как обычно говорят, логичное, мышление – это мышление по законам логики, по тем абстрактным схемам, которые фиксируются ими. Законы логики составляют тот невидимый каркас, на котором держится последовательное рассуждение и без которого оно превращается в хаотическую, бессвязную речь.

Формулировка закона противоречия

Из бесконечного множества логических законов самым популярным является закон противоречия. Он был открыт одним из первых и сразу же объявлен наиболее важным принципом не только человеческого мышления, но и самого бытия.

И вместе с тем в истории логики не было периода, когда этот закон не оспаривался бы и когда дискуссии вокруг него совершенно затихали бы.

Закон противоречия говорит о противоречащих друг другу высказываниях, т. е. о таких высказываниях, одно из которых является отрицанием другого. К ним относятся, например, высказывания «Луна – спутник Земли» и «Луна не является спутником Земли», «Трава – зеленая» и «Неверно, что трава зеленая» и т.п. В одном из противоречащих высказываний что-то утверждается, в другом – это же самое отрицается.

Если обозначить буквой А произвольное высказывание, то выражение не-А, будет отрицанием этого высказывания.

Идея, выражаемая законом противоречия, кажется простой и даже банальной: высказывание и его отрицание не могут быть вместе истинными.

Используя вместо высказываний буквы, эту идею можно передать так: неверно, что А и не-А. Неверно, например, что трава зеленая и не зеленая, что Луна спутник Земли и не спутник Земли и т.д.

Закон противоречия говорит о противоречащих высказываниях – отсюда его название. Но он отрицает противоречие, объявляет его ошибкой и тем самым требует непротиворечивости – отсюда другое распространенное имя – закон непротиворечия.

Мнимые противоречия

Большинство неверных толкований этого закона и большая часть попыток оспорить его приложимость, если не во всех, то хотя бы в отдельных областях, связаны с неправильным пониманием логического отрицания, а значит, и противоречия.

Высказывание и его отрицание должны говорить об одном и том же предмете, рассматриваемом в одном и том же отношении. Эти два высказывания должны совпадать во всем, кроме одной единственной вещи: то, что утверждается в одном, отрицается в другом. Если эта простая вещь забывается, противоречия нет, поскольку нет отрицания.

В романе Ф. Рабле «Гаргантюа и Пантагрюэль» Панург спрашивает Труйогана, стоит жениться или нет. Труйоган как истинный философ отвечает довольно загадочно: и стоит, и не стоит. Казалось бы, явно противоречивый, а потому невыполнимый и бесполезный совет. Но постепенно выясняется, что никакого противоречия здесь нет. Сама по себе женитьба – дело неплохое. Но плохо, когда, женившись, человек теряет интерес ко всему остальному.

Видимость противоречия связана здесь с лаконичностью ответа Труйогана. Если же пренебречь соображениями риторики и, лишив ответ загадочности, сформулировать его полностью, станет ясно, что он непротиворечив и может быть даже небесполезен. Стоит жениться, если будет выполнено определенное условие, и не стоит жениться в противном случае. Вторая часть этого утверждения не является, конечно, отрицанием первой его части.

Можно ли описать движение без противоречия? Иногда отвечают, что такое описание не схватило бы самой сути движения – последовательной смены положения тела в пространстве и во времени. Движение внутренне противоречиво и требует для своего описания оборотов типа: «Движущееся тело находится в данном месте, и движущееся тело не находится в данном месте». Поскольку противоречиво не только механическое движение, но и всякое изменение вообще, любое описание явлений в динамике должно быть – при таком подходе – внутренне противоречивым.

Разумеется, этот подход представляет собой недоразумение.

Можно просто сказать: «Дверь полуоткрыта». Но можно заявить: «Дверь открыта и не открыта», имея при этом в виду, что она открыта, поскольку не является плотно притворенной, и вместе с тем не открыта, потому что не распахнута настежь.

Подобный способ выражения представляет собой, однако, не более чем игру в риторику и афористичность. Никакого действительного противоречия здесь нет, так как нет утверждения и отрицания одного и того же, взятого в одном и том же отношении.

«Березы опали и не опали», – говорят одни, подразумевая, что некоторые березы уже сбросили листву, а другие нет. «Человек и ребенок, и старик», – говорят другие, имея в виду, что один и тот же человек в начале своей жизни – ребенок, а в конце ее – старик. Действительного противоречия в подобных утверждениях, конечно же, нет. Точно так же, как его нет в словах песни: «Речка движется и не движется... Песня слышится и не слышится...»

Те примеры, которые обычно противопоставляют закону непротиворечия, не являются подлинными противоречиями и не имеют к нему никакого отношения.

В «Исторических материалах» Козьмы Пруткова нашел отражение такой эпизод: «Некий, весьма умный, XIX века ученый справедливо тогдашнему германскому императору заметил: «Отыскивая противоречия, нередко на мнимые наткнуться можно и в превеликие от того и смеху достойные ошибки войти: не явное ли в том, ваше величество, покажется малоумному противоречие, что люди в теплую погоду обычно вхолодное платье облачаются, а вхолодную, насупротив того, завсегдатеплое надевают?» ...Сии, с достоинством произнесенные, ученого слова произвели на присутствующих должное действие, и ученому тому, до самой смерти его, всегда особливое внимание оказывалось».

Этот поучительный случай описывается под заголовком: «Наклонность противоречия нередко в ошибки ввести может». Применительно к нашей теме можно сделать такой вывод: наклонность видеть логические, противоречия там, где их нет, обязательно ведет к неверному истолкованию закона непротиворечия и попыткам ограничить его действие.

В оде «Бог» – вдохновенном гимне человеческому разуму – Г.Р.Державин соединяет вместе явно несоединимое:

...Я телом в прахе истлеваю,

Умом громам повелеваю,

Я царь – я раб, я червь – я бог!

Но здесь нет противоречия.

Противоречие «смерти подобно...»

Если ввести понятия истины и лжи, закон противоречия можно сформулировать так: никакое высказывание не является вместе истинным и ложным.

В этой версии закон звучит особенно убедительно. Истина и ложь – это две несовместимые характеристики высказывания. Истинное высказывание соответствует действительности, ложное не соответствует ей. Тот, кто отрицает закон противоречия, должен признать, что одно и то же высказывание может соответствовать реальному положению вещей и одновременно не соответствовать ему. Трудно понять, что означают в таком случае сами понятия истины и лжи.

Иногда закон противоречия формулируют следующим образом: из двух противоречащих друг другу высказываний одно является ложным.

Эта версия подчеркивает опасность, связанную с противоречием. Тот, кто допускает противоречие, вводит в свои рассуждения или в свою теорию ложное высказывание. Тем самым он стирает границу между истиной и ложью, что, конечно же, недопустимо.

Римский философ-стоик Эпиктет, вначале раб одного из телохранителей императора Нерона, а затем секретарь императора, так обосновывал необходимость закона противоречия: «Я хотел бы быть рабом человека, не признающего закона противоречия. Он велел бы мне подать себе вина, я дал бы ему уксуса или еще чего похуже. Он возмутился бы, стал бы кричать, что я даю ему не то, что он просил. А я сказал бы ему: ты не признаешь ведь закона противоречия, стало быть, что вино, что уксус, что какая угодно гадость: все одно и то же. И необходимости ты не признаешь, стало быть, никто не силах принудить тебя воспринимать уксус как что-то плохое, а вино как хорошее. Пей уксус как вино и будь доволен. Или так: хозяин велел побрить себя. Я отхватываю ему бритвою ухо или нос. Опять начинаются крики, но я повторил бы ему свои рассуждения. И все делал бы в таком роде, пока не принудил бы хозяина признать истину, что необходимость непреодолима и закон противоречия всевластен».

Так комментировал Эпиктет слова Аристотеля о принудительной силе необходимости, и в частности закона противоречия.

Смысл этого эмоционального комментария сводится, судя по всему, к идее, известной еще Аристотелю: из противоречия можно вывести все, что угодно. Тот, кто допускает противоречие в своих рассуждениях, должен быть готов к тому, что из распоряжения принести ему вина будет выведено требование подать уксуса, из команды побрить – команда отрезать нос и т.д.

Один из законов логики говорит: из противоречивого высказывания логически следует любое высказывание. Появление в какой-то теории противоречия ведет в силу этого закона к ее разрушению. В ней становится доказуемым все, что угодно, были смешиваются с небылицами. Ценность такой теории равна нулю.

Конечно, в реальной жизни все обстоит не так страшно, как это рисует данный закон. Ученый, обнаруживший в какой-то научной теории противоречие, не спешит обычно воспользоваться услугами закона, чтобы дискредитировать ее. Чаще всего противоречие отграничивается от других положений теории, входящие в него утверждения проверяются и перепроверяются до тех пор, пока не будет выяснено, какое из них является ложным. В конце концов, ложное утверждение отбрасывается, и теория становится непротиворечивой. Только после этого она обретает уверенность в своем будущем.

Противоречие – это еще не смерть научной теории. Но оно подобно смерти

28. Основные законы логики

Закон в научном знании представляет собой не что иное, как необходимую связь между теми или иными явлениями. С его помощью, зная одни из них, можно предвидеть, каковы будут другие, связанные с первыми. Логические законы представляют собой необходимые, нерасторжимые связи между мыслями и с их помощью, установив истинность (или ложность) исходных высказываний, можно определить истинность или ложность других, обусловленных необходимыми связями с первыми. Или иначе: признавая какое-то высказывание за истинное, мы вынуждены признавать и многие другие, вытекающие из него высказывания, а также отвергать те, которые несовместимы с ним. Впрочем, в практике умственной деятельности чаще приходится решать обратную задачу: имея уже выполненное рассуждение, проверить, в самом ли деле оно соответствует законам логики, то есть, вытекают ли сделанные в нем выводы из тех мыслей, которые взяты в нем за исходные. Знание законов логики и умение пользоваться ими избавляет от ошибок в рассуждениях, исключает необоснованные выводы, предохраняет от путаницы.

Как и во всякой иной науке, законов и правил логики очень много, даже неохватно много. Речь в данном случае пойдет только о самых первых, тех, по отношению к которым остальные являются производными. Три из них сформулированы Аристотелем: законзапретапротиворечия,законтождества,законисключенного третьего, четвертый закон –достаточного основания– выдвинут немецким математиком и философом семнадцатого-восемнадцатого веков Лейбницем.

Существует три фундаментальных свойства логической мысли - определенность,последовательностьиобоснованность. Они являются обязательными для мышления, когда оно занимается рассуждением. Основные законы логики отражают эти специфические черты мыслительной деятельности и в этом смысле производны от них.

Определенностьозначает, что любая вещь, ставшая предметом логического анализа, обязательно должна мыслиться в совокупности одних и тех же однажды выделенных признаков; они задаются при определении понятий, и не могут бесконтрольно изменяться в рамках одного и того же рассуждения.

Под последовательностьюпринимают то, что, приняв какое-либо положение за истинное, необходимо принимать и все вытекающие из него следствия, придерживаться их неукоснительно.

Обоснованностьотражает факт взаимозависимости любых мыслей от многих других; в логике можно рассматривать только такие высказывания, которые могут быть обоснованы, выведены из других положений. Содержание обоснованности раскрывается законом достаточного основания, в то время как другие фундаментальные свойства логической мысли выражаются через комбинацию остальных законов логики.

1. ЗАКОН ТОЖДЕСТВА.Всякая мысль тождественна самой себе, т.е. субъект рассуждений должен быть строго определен и неизменен до их окончания. Нарушением этого закона является подмена понятий (часто используется в адвокатской практике).

2. ЗАКОН НЕПРОТИВОРЕЧИЯ.Два противоположных суждения не могут быть одновременно истинны: по крайней мере одно из них ложно.

3. ЗАКОН ИСКЛЮЧЕННОГО ТРЕТЬЕГО.Истинно либо суждение, либо его отрицание ("третьего не дано").

4. ЗАКОН ДОСТАТОЧНЫХ ОСНОВАНИЙ.Для истинности всякой мысли должно быть достаточно оснований, т.е. умозаключение необходимо обосновать исходя из суждений, истинность которых уже доказана.

Объекты изучения логики.

Объектами изучения логики являются формы мышления:понятие, суждениеиумозаключение.

Понятие– это мысль, в которой обобщаются отличительные свойства предметов. Т.к. язык является формой выражения мысли, то в языке термину “понятие” соответствует “слово”. Но человек не мыслит отдельными понятиями. Выражая свои мысли, он составляет слова в предложения. Предложение в языке есть суждение в мыслях.

Суждение (высказывание) –есть мысль (выраженная в форме повествовательного предложения), в которой нечто утверждается о предмете действительности, которая объективно является либо истинной, либо ложной. Правда, истинность суждения относительна. Говорят, что суждение может иметь одно из двух значений истинности: “истина” или “ложь”. СУЖДЕНИЕ ИСТИННО (имеет значение истинности – истина), ЕСЛИ ОНО СООТВЕТСТВУЕТ ДЕЙСТВИТЕЛЬНОСТИ. Критерий истинности – практика (утверждал В.И.Ленин). К числу суждений не относятся мысли, не имеющие значения истинности. Таким мыслям в языке соответствуют вопросительные и побудительные предложения. Является ли суждением фраза: “Иванов сдаст экзамен на отлично”? Да, ведь это не вопросительное и не побудительное предложение. Но значение истинности его не определено, пока не пройдет экзамен.

Суждение, значение истинности которого не однозначно, называется гипотезой. Отношение к гипотезе среди ученых тоже было неоднозначным. Например Исаак Ньютон утверждал: “Hypotheses non fingo” – “Гипотез не измышляю”. М.В.Ломоносов же, напротив, писал, что гипотезы “дозволены в философских предметах и даже представляют собой единственный путь, которым величайшие люди дошли до открытия самых важных истин. Это – нечто вроде порыва, который делает их способными достигнуть знаний, до каких никогда не доходят умы низменных и пресмыкающихся во прахе...” Правда, была и оговорка: “Я не признаю никакого измышления и никакой гипотезы, какой бы вероятной она ни казалась, без точных доказательств”.

И, еще одно определение: закон науки– это суждение, истинность которого доказана.

Теорема– это предложение, истинность которого доказывается на основе аксиом или ранее доказанных теорем. Теоремы часто формулируются в виде импликаций (следования). Импликативная структура наиболее удобна для выделения условия и заключения теоремы (того, что дано, и того, что необходимо доказать). Если импликация А => В выражает некоторую теорему, то основание импликации А выражает условие, а следствие В – заключение теоремы. Условие или заключение в свою очередь может не быть элементарным высказыванием, а иметь определенную логическую структуру, чаще всего конъюнктивную(и, обозначается &) или дизъюнктивную (или, обозначается V). Рассмотрим примеры:

1. Теорема “Если диагонали параллелограмма взаимно перпендикулярны или делят его углы пополам, то этот параллелограмм - ромб” имеет структуру АVВ=>C, гдеА– “диагонали параллелограмма взаимно перпендикулярны”;В– “(диагонали параллелограмма) делят его углы пополам”;С– “этот параллелограмм - ромб”.

2. Теорема о средней линии трапеции имеет структуру: А=>В&С, гдеА– “четырехугольник – трапеция”;В– “его средняя линия параллельна основаниям”; С– “(его средняя линия) равна полусумме оснований”.

Часто в формулировках теорем используется выражение “необходимо и достаточно” (признак). В логике это выражение соответствует эквиваленции, которая, как известно, представима в виде конъюнкции двух импликаций. Одна из этих импликаций выражает теорему, доказывающую необходимостьпризнака, другая выражает теорему, доказывающуюдостаточностьпризнака. Например, признак перпендикулярности двух плоскостей:

“Для того чтобы две плоскости были перпендикулярны, необходимо и достаточно, чтобы одна из них проходила через прямую, перпендикулярную к другой”, может быть сформулирован и так: “Две плоскости перпендикулярны, ЕСЛИ И ТОЛЬКО ЕСЛИ одна из них проходит через прямую, перпендикулярную к другой”:

А <=> ВилиА => B & B =>A.

Умозаключение –это мысль, в ходе которой из одного или нескольких суждений выводится новое суждение.

При этом исходные суждения называются посылками, а полученное суждение –заключениемилиследствием. Аристотель приводил такой пример умозаключения: “Все люди смертны.” и “Сократ – человек.” - посылки. “Сократ смертен” – заключение. Переход от посылок к заключению происходит по правилом вывода и законам логики.

ПРАВИЛО 1: Если посылки умозаключения истинны, то истинно и заключение.

ПРАВИЛО 2: Если умозаключение справедливо во всех случаях, то оно справедливо и в каждом частном случае. (Это правило ДЕДУКЦИИ – переход от общего к частному)

Приведите пример дедуктивного вывода. С именем какого литературного героя связано понятие дедукции?

ПРАВИЛО 3: Если умозаключение справедливо в некоторых частных случаях, то оно справедливо во всех случаях. (Это правило ИНДУКЦИИ – переход от частного к общего.)

Всегда ли такой вывод справедлив? Приведите примеры верной и ошибочной индукции.

Цепи умозаключений складываются в РАССУЖДЕНИЯ и ДОКАЗАТЕЛЬСТВА, в которых заключение предшествующего умозаключения становится посылкой следующего. Условием правильности доказательства является не только истинность исходных суждений, но и истинность каждого входящего в его состав умозаключения. Доказательства должны быть построены по законам логики.

Познакомимся с некоторыми интересными видами умозаключений: умозаключение необходимо обосновать исходя из суждений, истинность которых уже доказана.

Паралогизм– умозаключение, содержащее непреднамеренную ошибку.Софизм– умозаключение, содержащее преднамеренную ошибку с целью выдать ложное суждение за истинное.

Попробуем, например, доказать, что 2 · 2 = 5:

4/4 = 5/5

4(1/1) = 5(1/1) – ошибка!

4 = 5.

Парадокс- это умозаключение, доказывающее как истинность, так и ложность некоторого суждения. Например: Генерал и брадобрей. Каждый солдат может сам себя брить или бриться у другого солдата. Генерал приказал выделить одного специального солдата-брадобрея, у которого брились бы только те солдаты, которые себя не бреют. Кто должен брить солдата? Кто должен брить солдата-брадобрея?

Аналогия

Аналогия в переводе с греческого означает сходство, подобие. Первоначально древние математики обозначали им пропорцию, однако со временем его смысловое значение расширилось. Помимо известных числовых соотношений аналогией стали называть отношения подобия у предметов самой различной природы. В настоящее время при нестрогом употреблении оно может означать всякое сходство вообще. Допустимо, например, говорить, что внутреннее строение атома аналогично устройству планетной системы, потому что в атоме электроны, подобно планетам, обращаются вокруг тяжелого ядра. Поведение пчелы, когда она вернулась с плодоносного участка, нередко уподобляют танцу; возможно, и в самом деле в нем выражается неудержимое удовлетворение, какое бывает и у людей, готовых, как говорится, плясать от восторга, и одновременно тем самым дается знать и другим пчелам о результатах поисков. Всякая модель, представляя собой копию оригинала, тоже является аналогией по отношению к нему.

В литературе и научных текстах аналогия иногда используется как художественный образ для придания наглядности тем или иным сообщениям.

Аналогия представляет собой вид умозаключения, в котором знания об одном предмете переносятся на предмет другой природы на основании наличия сходства между ними.

В логике, однако, при проведении аналогии не ограничиваются указанием на сходство. Оно становится основой для получения новых выводов о таких объектах, познание которых по каким-либо причинам затруднено. В таких случаях бывает полезно обратиться к другим, похожим в каком-либо отношении на интересующий нас. Когда у двух явлений (пусть даже природа того и другого существенно различна) имеется несколько подобных признаков, то тогда можно предположить, что сходство распространяется и дальше, на другие признаки, которые есть у одного, но пока не обнаружены у другого, однако со временем может быть все-таки откроются. Так, свойства колебательных движений сначала были изучены физикой только на примере волн, распространяющихся по поверхности воды. Потом, когда стало выясняться, что звук и свет тоже представляют собой колебания, то было естественно предположить, что у них тоже должна наблюдаться так называемая дифракция (огибание препятствий), причем формулы для ее расчета могут быть получены по аналогии с формулами для поверхностных волн. В дальнейшем это предположение полностью подтвердилось; проведенное уподобление одних волн другим оказалось, следовательно, эвристически продуктивным.

Доказательство

Доказательство как логическая ступень вбирает в себя все предыдущие формы мышления и в этом смысле оно является итоговой для всей науки о законах правильного мышления. И сама эта наука, собственно говоря, для того и создается, чтобы можно было с ее помощью строить доказательные рассуждения или проверять уже выполненные доказательства. Остальные ее разделы играют с этой точки зрения подчиненную, подготовительную роль. Определенность и последовательность в качестве фундаментальных свойств логической мысли (о них говорилось в разделе о законах логики) делают ее понятной, способной быть воспринятой другими, хотя этим еще не гарантируется, что с ней обязательно согласятся. Следующее же свойство, обоснованность, воплощаемое в доказательстве, превращает ее в единственно приемлемую для всех, принудительно принимаемую всяким, кто знаком с законами мышления. Правда, при непременном условии, что обоснование проведено без нарушений. Доказанное положение становится общепризнанной истиной, ее нельзя отклонять. По крайней мере, непризнание такого обоснованного всем предыдущим знанием положения обязывает к тому, чтобы подобное отношение к истине подкреплялось правильно построенным опровержением. Доказательство есть логическое действие, которое с помощью совокупности логических операций над понятиями, суждениями, умозаключениями показывает истинностное значение тех или иных высказываний.

Обоснование своим мыслям приходится давать каждому и ежедневно. В домашнем обиходе мы чаще всего опираемся на непосредственные наблюдения: “Ночью прошел дождь, потому что асфальт мокрый”, “Издание иллюстрированное, ведь это журнал мод”, “Раз растения на этом поле цветут колосками, значит оно засеяно злаковыми”. Такое подтверждение своих слов эмпирическими фактами и простейшими обобщениями тоже можно считать элементарной формой доказательства. Намного сложнее оно в научном познании, где надо вырабатывать теоретически обоснованные выводы и положения. Доказательство пронизывает науку, составляет ее ткань. В некотором смысле научная деятельность – одно большое доказательство. В ней постоянно проверяются и уточняются старые и новые истины. Без этого наука не была бы наукой. Само собой понятно, процессы доказательства в научном познании чрезвычайно усложняются. К общелогическим правилам и процедурам, которые изучаются в курсах логики, добавляется множество специфических, используемых только в конкретных отраслях знания.

Кроме того, научные истины часто идут вразрез с обыденным опытом. Так, благодаря долгим астрономическим наблюдениям было доказано, что движение Солнца по небу не более чем иллюзия. А физика после тщательного изучения явлений микро- и макромира пришла к удивительному, парадоксальному открытию: течение времени зависит от скорости движения. И в настоящее время в физической науке считается общепризнанным, что всякая новая теория должна быть достаточно “сумасшедшей” в том смысле, что она должна обязательно расходиться с так называемым здравым смыслом, и это является критерием ее новизны и научности.

Дело здесь в том, что наше сознание вместе со всеми привычными для него представлениями о пространстве, времени, причинности и прочем сформировалось под влиянием практики, которая, как сказал однажды В.И. Ленин, миллиарды раз приводила мышление к повторению одних и тех же фигур, дабы они приобрели значение аксиом. Но этот привычный для нас мир, сформировавший наш здравый рассудок, теперь уже – вчерашний день для большой науки. Началось проникновение в миры неизведанные, стало быть, и законы в них иные, “странные”, к которым наше сознание должно будет долго приноравливаться. Сказанное относится не только к естествознанию. Было бы более чем нелепо, если бы, например, хирург вынужден был доказывать пациенту, что без его вмешательства, скажем при аппендиците или какой-нибудь тяжелой травме, тот просто-напросто расстанется со своей жизнью. Ведь доказательство в подлинном смысле слова может опираться только на основательные познания, а подчас к ним надо еще и добавить опыт работы по данной медицинской специальности. Тем, у кого их нет, в общем-то, приходится полагаться на квалификацию специалистов и не более того. Да и в других областях знания, скажем в политике или делах общественного устройства, далеко не всегда можно полагаться на очевидность. Каких-то запредельных, неведомых миров здесь, конечно, нет. Тем не менее, то, что понятно рядовому обывателю, порой не выдерживает критики при более внимательном изучении. Не то, чтобы его взгляды насквозь ошибочны. Просто истины, непосредственно лежащие на поверхности, именно поэтому давным-давно воплотились в жизнь, а то, что может ее еще дальше улучшить, уже не является столь очевидным для всех и именно поэтому с трудом открывается и пробивает себе дорогу. Вообще многим часто кажется, что истина в качестве отражения действительности навязывается сама собой, в то время как заблуждение – плод чьих-то искажающих эту действительность усилий. На самом деле легко впасть именно в заблуждение. Доказательство же истины всегда сопряжено с поисками, подчас трудными и долгими.

Структура доказательства

В любом доказательстве имеется три компонента: тезис – положение, которое собираются доказать, аргументы – утверждения, из которых тезис выводится по правилам логики (их называют также основаниями), и демонстрация (или форма доказательства) – само рассуждение, показывающее связь между аргументами и тезисом.

Правдоподобные рассуждения

Согласно логике высказываний, можно утверждать, что

Из АследуетВ

Аистинно

_____________

Вистинно

В обратной ситуации, когда мы знаем об истинности В и его следствии из А, однозначно утверждать, что А также истинно нельзя.

и

Из АследуетВ

Вложно

_____________

Аложно

В обратной ситуации, когда мы знаем об истинности В и его следствии из А, однозначно утверждать, что А также истинно нельзя.

29. Рассуждение, умозаключение

Учение о рассуждении, о логическом выводе является основой формальной логики. Убеждения присущи каждому человеку, они сопровождают его на протяжении всей жизни. С одной стороны, это достаточно устойчивая категория и многие люди сохраняют свои убеждения в неизменном виде, а кто-то легко расстается со своими убеждениями. Примеров в истории человечества достаточно. Сотни, тысячи, а иногда и миллионы людей удавалось убедить в том, что те или иные их действия приведут к искомому результату. И эти люди шли на любые лишения, безоговорочно ориентируясь на свои убеждения. Есть и противоположные примеры, когда люди с каким-то ожесточенным упорством не желают признавать простейшие истины. И тот, и другой результат достигается с помощью рассуждений по тому или иному вопросу. К рассуждению относится любое устное выступление, любая статья, зафиксированная на каком-либо носителе информации.

Рассуждение – это акт коммуникации, состоящий в планомерном преобразовании определенных структур языкового мышления некоторого субъекта с целью изменения соответствующих структур другого субъекта.

В рассуждении выделяют:

• наличие объекта, т. е. рассуждение о чем-то, предметность;

• опора на запас знаний субъекта, его навыки, его психологические особенности, т. е. доступность, активность адресата, при­емлемость для него, учет его особенностей;

• эвристичность, т. е. обнаружение новых неизвестных характеристик или обоснование сомнительных характеристик объекта, отсюда, доказательность, нацеленность, тезисность рассуждения;

• информативность, т. е. приобретение новых знаний, интерес, новизна;

• взаимодействие анализа и синтеза, т. е. соучастие в процессе мышления, ведение за своей логикой;

• планомерность влияния на адресата.

Главными характеристиками рассуждений являются убедительность и доказательность:

• недоказательная убедительность – характеристика рассуждений, не удовлетворяющих логическим стандартам доказа­тельности, но, тем не менее, признаваемых приемлемыми в рамках некоторой теории или культурной парадигмы;

• неубедительная доказательность – характеристика рассуждений, которые внешне удовлетворяют логическим стандартам доказательности и в то же время слишком сложны (запутанны, длинны) для того, чтобы субъект познания на данном уровне логической компетенции мог оценить их правильность;

• убедительная доказательность – характеристика рассуждений, которые имеют доказательство с прозрачной, эффективной структурой;

• доказательная убедительность – характеристика рассуждения, в котором снижается сложность первоначального высказывания при помощи «локальных» преобразований его структуры и в результате доказательство исходного высказывания.

Основное требование к рассуждениям – это соблюдение формально-логических законов и правил мышления.

Исследованием способов изменения убеждений занимается теория аргументации. Приемы, с помощью которых могут формироваться и изменяться убеждения, разнообразны и разнородны. Наиболее распространенные способы убеждения делятся на универсальные, применимые во всякой аудитории, и контекстуальные, эффективные лишь в некоторых аудиториях. К универсальным относятся эмпирические и теоретические аргументы, к контекстуальным – ссылки на традицию, здравый смысл и т. п.

Эмпирические способы аргументации опираются по преимуществу на опыт. Теоретическая аргументация основывается на рассуждении.

Эмпирические способы обоснования называются также подтверждением.

Оно подразделяется на прямое и косвенное.

Прямое подтверждение – это непосредственное наблюдение тех явлений, событий, о которых говорится в проверяемом утверждении.

Косвенное подтверждение — это подтверждение в опыте логических следствий обосновываемого положения.

Прямое подтверждение возможно лишь в случае утверждений о единичных объектах или ограниченных их совокупностях. Теоретические положения обычно касаются неограниченных множеств предметов.

В науке непосредственное наблюдение того, о чем говорится в проверяемом утверждении, редкость. Более важным и универсальным способом подтверждения является выведение из обосновываемого положения логических следствий и их последующая опытная проверка. Подтверждение следствий оценивается при этом как свидетельство в пользу истинности самого положения. Чем большее число следствий нашло подтверждение, тем выше вероятность проверяемого утверждения. Поэтому важно выводить из выдвигаемых и требующих надежной основы положений как можно больше логических следствий с целью их проверки.

Способы теоретической аргументации разнообразны и разнородны. Один из них – это выполнение условия совместимости.

Согласно условию совместимости обоснованное утверждение должно находиться в согласии с принятыми в рассматриваемой области общими положениями, принципами, концепциями и т. п. Принцип простоты требует использовать при объяснении изучаемых явлений как можно меньше независимых допущений, которые должны быть возможно более простыми. Принцип привычности рекомендует избегать неоправданных новаций и стараться, насколько это возможно, объяснять новые явления с помощью известных законов.

Другим способом теоретического обоснования является анализ утверждения с точки зрения возможности эмпирического его подтверждения и опровержения. Новые положения должны допускать принципиальную возможность опровержения и использования определенных процедур своего подтверждения.

Обоснование всегда носит системный характер. Включение нового положения в систему других положений, придающую устойчивость своим элементам, является одним из наиболее важных способов в его обосновании. Подтверждение следствий, вытекающих из теории, одновременно подкрепляет и саму теорию. Включив анализируемое положение в теорию, мы, тем самым, распространяем на него ту эмпирическую и теоретическую поддержку, какой обладает теория в целом. Поскольку теория сообщает входящим в нее утверждениям дополнительную поддержку, совершенствование теории, укрепление ее эмпирической базы и прояснение ее общих, в том числе философских, предпосылок одновременно является вкладом в обоснование входящих в нее утверждений. К способам теоретического обоснования относится также проверка выдвинутого положения на приложимость его к широкому классу исследуемых объектов.

Объяснение и понимание являются универсальными операциями человеческого мышления, применимыми во всех областях.

Объяснение – это рассуждение, посылки которого содержат информацию, достаточную для выведения из нее рассматриваемого факта или события.

Наиболее развитая форма научного объяснения – это объяснение на основе теоретических законов. Законы обеспечивают не только объяснение наблюдаемых фактов, но служат также средством предсказания новых, еще не наблюдавшихся фактов. Предсказание факта – это, как и объяснение, выведение его из уже известного закона.

Другой операцией мышления является понимание, связанное с усвоением нового содержания, включением его в систему устоявшихся идей и представлений. Понимание – универсальная операция. Как и объяснение, оно имеется во всех науках. Понимание разных вещей имеет разную ценность для человека. Поэтому понимание можно определить, как оценку на основе некоторого образца, стандарта или правила. Если объяснить – значит вывести из имеющихся общих истин, то понять – значит вывести из принятых общих ценностей.

Универсальная аргументация, о которой шла речь, не исчерпывает всех способов. Контекстуальная аргументация может быть убедительной для тех, кто придерживается тех же верований, признает те же авторитеты или традиции и одновременно кажется неубедительной для людей других убеждений, опирающихся на иные авторитеты и традиции.

Из всех контекстуальных аргументов наиболее распространен аргумент к традиции. Внимание людей к приводимым аргументам определяется теми традициями, которые они разделяют. Традиция имеет отчетливо выраженный описательно-оценочный характер. Она представляет собой анонимную, стихийно сложившуюся систему образцов, норм, правил и т. п., которой руководствуется в своем поведении достаточно большая и устойчивая группа людей. Обращение к традиции для поддержки выдвигаемых положений – это обычный способ аргументации в обществах, где традиция и традиционализм ставятся если не выше разума, то, по меньшей мере, наравне с ним. Обращение к традиции – это обычный способ аргументации в морали. Повседневная жизнь во многом ориентируется на традицию, и обращение к ней – это стандартный прием практической аргументации.

Аргумент к авторитету – это ссылка на мнение или действие лица, признанного в данной области своими суждениями или поступками.

Ссылка на авторитет, на сказанное или написанное кем-то не относится к универсальным способам обоснования. Авторитеты нужны, в том числе в научной сфере. Возможности отдельного человека ограничены, он не в состоянии все самостоятельно проверить и проанализировать. Но полагаться на мнения и рассуждения других людей нужно не потому, что это сказал именно этот человек, а потому, что сказанное является правильным.

Здравый смысл можно охарактеризовать примерно как общее, присущее каждому человеку чувство истины и справедливости, приобретенное жизненным опытом. Здравый смысл проявляется в рассуждениях о правильном и неправильном и применяется он в общественных и практических делах. С изменением общественной жизни меняется и представление о здравом смысле.

Интуицию определяют как прямое усмотрение истины, постижение ее без всякого рассуждения и доказательства. Для интуиции характерны неожиданность, неверостность, неосознанность ведущего к ней пути. Она всегда является результатом большой предварительной работы ума и души человека. В этом смысле интуитивное познание доступно лишь людям одаренным, трудолюбивым и целеустремленным.

Вера – это глубокое, эмоционально насыщенное убеждение в справедливости какого-либо положения.

Она всегда субъективна. Человек принимает какие-то положения за доказанные без обсуждения.

Аргументация к вкусу – это обращение к чувству вкуса, имеющемуся у аудитории и способному склонить ее к принятию выдвинутого положения.

Вкус касается только совершенства каких-то вещей и опирается на непосредственное чувство, а не на рассуждение. Вкус – это не простое своеобразие подхода человека к оцениваемо­му им явлению. Вкус всегда претендует на общую значимость. Это проявляется чаще всего в феномене моды, тесно связанном со вкусом. Мода касается быстро меняющихся вещей, явлений и воплощает в себе не только вкус, но и определенный, общий для многих способ поведения.