Конспект лекций Высшая математика (Басканова)

329

Далее следует отметить, что вычисление линейного интеграла с помощью неопределенного по формуле Ньютона-Лейбница на практике не всегда возможно. Во-первых, первообразная может не выражаться через известные элементарные функции, т.е. не берется соответствующий неопределенный интеграл, либо первообразная не выражается через известные неэлементарные (специальные) функции. Во-вторых, найденная первообразная может оказаться очень громоздкой. И, наконец, функция, которую надо проинтегрировать, может быть задана не формулой, а например, таблицей значений или графиком. Во всех этих случаях линейный интеграл вычисляют приближенно с помощью численного интегрирования. Существует много различных способов и формул для приближенного вычисления линейного интеграла. Мы здесь рассматривать их не будем.

3.7.3. Интегрирование по частям в линейном интеграле

Нахождение первообразной методом интегрирования по частям в линейном интеграле проводят по той же формуле, что и в неопределенном интеграле:

b b

ud u b du.

Разница заключается лишь в том, что для линейного интеграла находят не саму первообразную, а ее приращение на интервале интегрирования [α,b].

2

Пример 6. Вычислить интеграл xcos xdx .

0

Решение. Разобьем на части подынтегральное выражение

		u x;	d cos xdx
2 xcos xdx							xsin x				0 2		2 sin dx
		du dx;		sin x
0													0
2 xcos xdx xsin x cos x						0 2 sin		cos				0sin 0 cos0
0						2	2		2
2 xcos xdx		1 3,14		1 0,57
0	2		2

В данном случае соответствующий неопределенный интеграл берется. Значение линейного интеграла найдено по формуле Ньютона-Лейбница.

3.7.4. Замена переменной интегрирования в линейном интеграле

330

Переход к новой переменной интегрирования в определенном интеграле проводят по формуле:

b		x (t)		t2
f (x)dx		dx (t)dt
		(t )			f (t) (t)dt (3.7.8)
		1		t1
		b (t2)

где функция х = φ(t) – должна быть дифференцируемой, а обратная t = ψ(х) – однозначной. Подынтегральное выражение в формуле (3.7.8) преобразуется так же, как в неопределенном интеграле. Однако очень важно подчеркнуть, что одновременно с преобразованием подынтегрального выражения, следует пересчитать пределы интегрирования, так как у новой переменной t будут другие границы изменения. Эти границы находят из уравнений:

(t1)

b (t2 )

Уравнения получают путем подстановки х = α, х = b в функцию х = ψ(t). Возвращаться к старой переменной x, как это было в случае неопределенного интеграла, здесь не нужно.

	8	x 1
	Пример 5. Вычислить интеграл:		dx .
	0	x 3

Чтобы избавиться от корня, возьмем его за новую переменную:

8	x 1		x 1 t								dx 2tdt									3				t										3 t2dt
		dx	x 1 t2								0 1 t																			2tdt 2
0																				1														1 t2 2
	x 3																1					(t2 1) 3
			x t2 1								8 1 t2
8	x 1		3	t	2		2			2					3	t	2		2					3				dt
		dx	2								dt			2							dt 4
	x 3					t	2	2									2		2								2	2
0			1												1 t									1 t
8	x 1		3					3		dt								13		4							t					3
		dx 2 dt 4											2t										arctg
	x 3									2
0			1					1 t				2									2							2				1
8	x 1					4						3									1
		dx 4						arctg							arctg
	x 3						2						2								2
0
В приведенном примере новые пределы интегрирования t1																																					0 1 1

и t2 8 1 3 определяются однозначно, так как за новую переменную t

взяты только положительные значения корня: t	x 1 , т.е. функция t =
ψ(х) – однозначна.

331

3.7.5. Несобственные линейные интегралы

Определенный линейный интеграл существует, если выполнены два условия, а именно:

1.интервал интегрирования конечен;

2.подынтегральная функция в интервале интегрирования нигде не обращается в бесконечность.

Такие определенные интегралы называют интегралами в собственном смысле этого слова, или собственными. Однако, иногда приходится иметь дело с интегралами, у которых нарушено одно из этих условий. Они получили название несобственных. Перейдем к их рассмотрению.

3.7.5.1. Линейные интегралы с бесконечными пределами (несобственные интегралы первого рода)

Дан определенный линейный интеграл:

b

f (x)dx

у которого f(x) – непрерывна на всей числовой оси ( ; ) , и интервал

интегрирования [α,b] – конечен. Пусть одна из границ интервала [α,b], или обе стремятся к бесконечности. Тогда пределы:

	b
lim		f (x)dx		f (x)dx
b
	b		b
		f (x)dx			f (x)dx
lim
	b
lim		f (x)dx			f (x)dx
b

называют несобственными интегралами первого рода, или интегралами с бесконечными границами.

Если эти пределы равны конечному числу, то в таких случаях говорят, что несобственные интегралы первого рода сходятся.

Если пределы не существуют или равны бесконечности, то несобственные интегралы расходятся (не существуют).

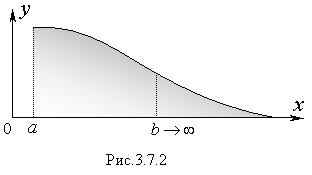
Геометрически, сходящийся несобственный интеграл первого рода, представляет собой конечную площадь фигуры бесконечной протяженности. Иллюстрировать это можно следующим образом.

332

Рассмотрим интеграл f (x)dx . График подынтегральной функции

схематически представлен на рисунке 3.7.2. При x → ∞ f(x)→ 0.

Поэтому увеличение площади при больших «b» становится ничтожно мало, в результате площадь бесконечно протяженной фигуры может

быть конечной.

Несобственные интегралы первого рода с одной бесконечной границей находят по формулам:

			b	f (x)dx lim F(b) F( )
		f (x)dx lim
			b	b
b			b		F(b) F( )
		f (x)dx	lim	f (x)dx lim

Поскольку под знаком пределов стоят определенные интегралы с конечными границами, их можно вычислять по формуле Ньютона-Лейбница (при условии, что соответствующий неопределенный интеграл берется), а затем найти предел полученного выражения.

Вычисление интеграла, у которого обе границы бесконечны, сводят к вычислению суммы двух несобственных интегралов с одной бесконечной границей:

				0
			f (x)dx f (x)dx f (x)dx
							0
Рассмотрим несколько примеров.
Вычислить несобственные интегралы:
		b		е 3х		b		1			1				1
1.	е 3хdx lim	е 3	хdx lim				lim
				3				3e	3b		3e	0			3
0	b	0	b		0		b

Интеграл сходится.			sin5x b
		b					sin5b sin 0
2. cos5xdx lim		cos5xdx lim		5			lim	5
0	b	0	b			0	b

Функция sin5b при b не имеет предела, интеграл расходится.

333

dx

lim

b dx

lim

b

ln b ln1

3.

ln x 1 lim

1 x

b

1 x

b

b

Интеграл расходится.

dx

0

dx

dx

4.

2

2

1

x

2

1

x

1

x

0

Вычислим каждый из двух интегралов с одной бесконечной границей:

0

dx

0

dx

0

lim

lim arctgx

lim (arctg0

arctga)

1 x2

1

x2

2

dx

b

dx

b

lim

lim arctgx 0

lim (arctgb arctg0)

1 x

2

1

x

2

2

0

b

0

b

b

Складывая найденные значения двух несобственных интегралов, полу-

чим:

dx

2

2

1 x

2

Данный интеграл сходится.

3.7.5.2 Линейные интегралы от разрывных функций (несобственные интегралы второго рода)

b

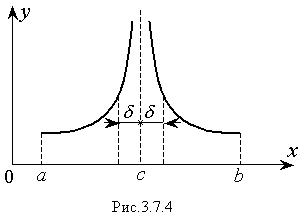
Рассмотрим интеграл f (x)dx у которого интервал [α,b] конечен, а по-

дынтегральная функция f(x) – терпит разрыв второго рода в одном из концов интервала (Рис.3.7.3).

Изолируем точки бесконечного разрыва δ – окрестностью и рассмотрим такие пределы:

	b		b
lim		f (x)dx		f (x)dx
0

334

	b		b
lim		f (x)dx		f (x)dx
0

Эти пределы называют несобственными интегралами второго рода. Разрыв в одном из концов интервала обозначен символом «–».

В случае конечных пределов, говорят, что несобственные интегралы сходятся.

Если пределы не существуют или равны бесконечности, то несобственные интегралы расходятся.

Подынтегральная функция может иметь бесконечный разрыв в промежуточной точке х = с интервала [α,b] (Рис. 3.7.4). Интеграл от такой функции разбивают на два несобственных интеграла второго рода:

b

c

b

f (x)dx f (x)dx f (x)dx, α < c < b,

c

Если оба интеграла в правой части равенства сходятся, то сходится и

b

интеграл f (x)dx; этот интеграл расходится, если расходятся хотя бы один

из интегралов справа.

Сходящимся несобственным интегралам второго рода также можно придать определенный геометрический смысл: они равны конечной площади фигур бесконечной протяженности.

Интегралы от разрывных функций вычисляют по формулам, аналогичным для интегралов с бесконечными пределами:

b		b		F(b) F( )
	f (x)dx lim		f (x)dx lim
	0		0
b		b		F(b ) F( )
	f (x)dx lim		f (x)dx lim
	0		0

Покажем на примерах применение этих формул.

335

	1	dx
	Пример 5. Вычислить несобственный интеграл		.
	0	1 x

Решение. Подынтегральная функция обращается в бесконечность при x = 1. Изолируем точку разрыва и найдем предел:

1	dx			1		dx					1
		lim					lim		1 x
	1 x					1 x		2				0
0		0		0			0
	lim		2		1 1 2			1 0		2
		0

Интеграл сходится, т.е. существует.

												1
Пример 6. Вычислить несобственный интеграл dx2 .
												0	x
							1
Решение. Функция			f (x)					терпит разрыв второго рода в начале ин-
						x2
тервала [0,1]. Отступим от точки разрыва и найдем предел:
1	dx			1	dx			lim		1 1	lim			1
	x	2 lim					2					1
0			0	0 x				0		x	0

Данный интеграл расходится, или не существует.

3.7.5.3. Признаки сходимости несобственных интегралов

В приведенных выше примерах существование несобственных интегралов определялось путем отыскания предела приращения первообразной. Как уже отмечалось, первообразная не всегда легко находится, а иногда вообще не выражается через элементарные функции. В таких случаях сходимость несобственных интегралов определяют по признакам сходимости, которые почти одинаковы для интегралов первого и второго рода.

Сформулируем сначала первый признак существования несобственных интегралов для неотрицательных функций.

Интегралы первого рода	Интегралы второго рода
Пусть две неотрицатель-	Пусть две неотрицательные
ные функции f(x) и φ(x) непре-	функции f(x) и φ(х) на интервале
рывны на интервале [α,∞).	[α,b] терпят бесконечный разрыв в
	точке b.
Если f(x) ≤ φ(х) на [α,∞), и	Если f(x)≤φ(x) на [α,b] и ин-
	b
интеграл (x)dx - сходится, то	теграл (x)dx - сходится, то схо-

	336
	b
сходится и f (x)dx.	дится и f (x)dx.
Если f(x)≥φ(x) на [α,∞) и	Если f(x)≥φ(x) на [α,b], и ин-
	b
интеграл (x)dx - расходится,	теграл (x)dx - расходится, то
	b
то интеграл f (x)dx –	интеграл f (x)dx – также расхо-
также расходится.	дится.

Признак доказывается на основании интегрирования неравенств. Чтобы пользоваться указанным признаком, нужно иметь набор функций, с которыми сравнивают подынтегральную, и сходимость или расходимость интегралов от которых известна. Для несобственных интегралов первого рода по-

дынтегральную функцию сравнивают с функцией (x)

1

, интеграл от ко-

торой:

xn

сходится при

n 1

dxn

расходится

при n 1

x

Для интегралов второго рода подынтегральную функцию, разрывную в

1

нижнем конце интервала, сравнивают с функцией (x)

, интеграл

(x )n

от которой:

b

dx

сходится

при

n 1

)

n

расходится

при

n 1

(x

Если подынтегральная функция терпит бесконечный разрыв в верхнем

1

конце интервала, то ее сравнивают с функцией (x)

, интеграл от

(b x)n

которой:

b

dx

сходится

при

n 1

x)

n

расходится

при

n 1

(b

Покажем это. Вычислим несобственные интегралы от эталонных функ-

ций.

x1 n b

dx

b1 n

1 n

xn

lim

lim

b 1 n

b 1 n

1 n

Полученный предел будет равен бесконечности, если показатель степени 1 – n > 0 или n < 1, интеграл расходится.

337

Если же 1 – n < 0 или n > 1, то выражение b1 n будет бесконечно малой величиной. Следовательно, при n >1 интеграл сходится. Осталось выяснить вопрос сходимости данного интеграла при n = 1.

dx

b

ln .

Интеграл расходится.

x

lim ln x lim ln b

b

b

1

Рассмотрим следующий интеграл от функции

(x)

:

(x )n

b

dx

(x )1 n

b

(b )1 n

1 n

lim

lim

(x )n

1 n

1 n

0

0

1 n

В правой части последнего равенства 1 n будет бесконечно малой, если 1 – n > 0, т.е. при n < 1 интеграл сходится, а при 1 – n < 0, или при n > 1 расходится. Для n = 1 интеграл также расходится:

b dx

b

b

lim

ln(x

)

lim ln

x

0

0

И, наконец, вычислим несобственный интеграл от функции

1

:

(b x)n

b

dx

(b x)1 n

b

1 n

(b )1 n

lim

lim

(b x)n

1 n

1 n

0

0

1 n

Из полученного выражения следует: если 1 – n >0, n < 1 интеграл сходится, если 1 – n < 0, n > 1 – интеграл расходится.

Рассмотрим несколько примеров на применение данного признака. Определить сходимость или расходимость интегралов.

dx

1.

; Сравним

подынтегральную

функцию

с

функцией

x

2

(1 e

x

)

1

1

(x)

,

интеграл

от

которой

dx2 сходится

(n = 2 >

1).

Так как

2

x

1

x

1

1

f (x)

, то данный интеграл также сходится.

x2 (1 ex )

x2

dx

2.

; Эталонную функцию выберем следующим образом

1 x 3 1

1

x2

, для которой n 7 1.

(x)

1

1

1

x 3

x 12 x23

x7 6

x2

6

Подынтегральная функция меньше эталонной:

338

f (x)

1

1

, интеграл сходится, или существует.

1 x 3 1 x2

x 3 x2

xdx

3.

; Сравним подынтегральную функцию:

1

1

x

f (x)

x

x

1

1

; n 1

1 интеграл расходится или не

2x 12

существует.

1 x

2x

2 x

2

1

dx

4.

;

В нижнем конце интервала подынтегральная функция

x 4x

3

0

терпит разрыв второго рода, сравним ее с функцией (x)

1

1

(x

0)n

xn

f (x)

1

1

1

, так как n

1 1, интеграл сходится.

x 4x3

x 12

1

x

2

dx

5.

; Функция,

стоящая под знаком интеграла,

обращается в

1 x2

0

бесконечность в верхнем конце интервала. Поэтому сравним ее с функцией

вида: (x)	1
	(1 x)n
f (x)	1				1		1	;	n	1	1, интеграл сходится.
		1 x2			1 x		(1 x)12			2

Как уже отмечалось, первый признак сходимости применим для несобственных интегралов от неотрицательных функций. Если подынтегральная функция меняет знак, сходимость несобственных интегралов оценивают по второму признаку. Приводим его формулировку.

		Для интегралов первого					Для интегралов второго рода
				рода
Пусть					знакопеременная	Пусть			знакопеременная
функция f(x) непрерывна на ин-						функция f(x) на [α,b] терпит раз-
тервале [α,∞).						рыв 2 рода в точке х = b.
Если сходится интеграл от						Если сходится инте-
абсолютной величины функции						b
						грал	f (x)	dx, то сходится и инте-
		f (x)		dx,	то сходится и
						b
						грал f (x)dx.