Конспект лекций Высшая математика (Басканова)

239

Лекция 2.14. ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКА

Одним из приложений производной является её применение к исследованию функций и построению графика функции.

Полное исследование функции одной переменной проводят по следующей схеме.

1.Область определения, область значений функции.

2.Непрерывность функции, точки разрыва и их род.

3.Асимптоты графика функции.

4.Симметрия графика функции (четность, нечетность).

5.Периодичность.

6.Точки пересечения графика с осями координат, промежутки знакопостоянства.

7.Интервалы монотонности, экстремумы.

8 Интервалы выпуклости и вогнутости, точки перегиба.

9 Если есть необходимость, для более точного построения графика найти значения функции в некоторых точках области определения.

Построение графика производят по результатам исследования.

2.14.1. Асимптоты графика

y

	y=f(x)
	M
	d
0	x0	x

рис. 2.14.1

lim f x , или

x x0 -0

Определение. Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремиться к нулю при неограниченном удалении от начала координат этой точки по кривой (рис. 2.14.1).

Асимптоты бывают вертикальными, наклонными и горизонтальными.

Прямая x x0 является вертикальной асимпто-

той графика функции y f x , если lim f x , или

x x0

lim f x . Иначе говоря, вертикальные асимптоты

x x0 0

расположены в точках бесконечного разрыва функции (в точках разрыва II – го рода).

	Пример. Функция					y	1			терпит разрыв в точке x 1, т.к.
							x 1				0
	1			1
lim			и lim			, то x					1 – точка разрыва II-го рода.
x 1 0 x 1			x 1 0 x 1							0
	Следовательно, прямая x 1							– вертикальная асимптота.

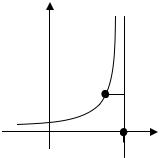
240

Если при x функция y f x неограниченно возрастает или убывает, приближаясь к прямой y kx b , то данная прямая является наклонной

асимптотой.
Найдем k и b .
Пусть M x; y	– произвольная точка кривой y f x (см. рис. 2.14.2).
y			Найдем расстояние от точки M до прямой							y kx b
			по формуле:
y=f(x)
M(x;y)			d			kx y b			.
						k2 1
d
			По определению асимптоты d 0 . Это возмож-
0		x	но лишь тогда, когда числитель дроби стремится к ну-
рис. 2.14.2			лю, т.е.							(2.14.1)
			lim kx y b 0 .
			x

1. По теореме 7 п.2.3.3 из (2.14.1) следует, что kx y b , где – бесконечно малая ( 0 при x ). Таким образом y kx b .

		Рассмотрим предел отношения						y	, при x :
								x
	y		kx b		b
lim		lim	x	lim k	x				k , т.е.
x x		x		x			x

k lim

f

x

.

(2.14.2)

x

x

2.

Предел

(2.14.1)

представим

как

сумму

пределов

lim

kx y lim b 0 , т.е. lim

kx y b 0 . Отсюда b lim

kx y или

x

x

x

x

x

b lim

f

x

kx

.

(2.14.3)

Замечание. Если хотя бы один из пределов (2.14.2) или (2.14.3) не существует или равен бесконечности, то график функции y f x наклонной

	асимптоты не имеет.	x2
	Пример. Найти наклонную асимптоту графика функции y			, если
		x	2
	она существует.
	Решение: Найдем k и b по формулам (2.14.2) и (2.14.3).

k lim

x2

lim

x

1,

x 2

x x

x x 2

x2

x2 x2 2x

2x

b lim

1 x

lim

lim

2.

x x-2

x

x 2

x x 2

241

Тогда наклонная асимптота существует и её уравнение имеет вид y x 2 .

Ответ: y x 2 .

Горизонтальная асимптота y b – прямая, параллельная оси OX ,

существует при k 0. Тогда

b lim f x .	(2.14.4)
x
Замечание. Асимптоты графика функции y f x	при x и при

x могут быть разными. Поэтому при нахождении пределов (2.14.2), (2.14.3) и (2.14.4) следует отдельно рассматривать случай, когда x и когда x .

2.14.2. Интервалы монотонности. Экстремумы функции

Теорема 1. Функция			y f x , дифференцируемая на интервале					a;b
возрастает	(убывает) на		этом интервале		тогда	и только	тогда,	когда
f x 0 f x 0		для всех точек x a;b .
Доказательство:
1. Докажем необходимость.
Пусть f x		– монотонно		возрастает на		интервале	a;b .	Точке
x a;b	зададим	приращение		x 0 .	Тогда	f x x f x		, т.е.

	f x x f x	0 . Поэтому	f x	lim	f	x x f x		0 . Ч. и т. д.
	x			x 0		x
2. Докажем достаточность.
	Пусть f x 0 при любом x a;b . Рассмотрим две точки								x1 и	x2
x1 x2 , принадлежащие интервалу				a;b .		На отрезке x1; x2 к функции
	f x применим формулу Лагранжа (п.2.12.3):
		f x2 f x1 f c x2 x1 , где x1					c x2 .
	Так как f c 0 , то		f x2 f x1 0 , т.е.				f x2 f x1 ,		значит
функция f x – возрастающая.				Ч. и т. д.
	Определение. Точка, в которой производная функции равна нулю или
не существует, называется критической точкой.
	Определение. Точка x0		из области определения функции y f x							на-

зывается точкой минимума (максимума) этой функции, если существует

такая –окрестность точки	x0 , что	для всех x из этой –окрестности вы-
полняется неравенство f x	f x0	f x f x0 (см. рис. 2.14.3, 2.14.4).

Точки максимума и минимума функции называются точками экстремума

242

функции, а значения функции в этих точках называются соответственно

максимумом и минимумом функции, или экстремумами функции.

Замечание. Из определения следует, что экстремумы функции носят

y
f(xi)		y=f (x)
f (x0)
	(	)	x
0	x0–	x0 xi x0+δ

y

f(x0) f(xi)

0

(	)	x
x0–δ	x0 xi x0+δ

рис.2.14.3

рис. 2.14.4

локальный характер – это наименьшее или наибольшее значения функции, по сравнению с ближайшими её значениями, принимаемыми в точках из - окрестности точки экстремума.

Замечание. Если функция y f x задана на отрезке a;b , то точки a

и b не могут быть точками экстремума, так как у них не существует – окрестностей, принадлежащих области определения данной функции.

Имеют место теоремы.

Теорема 2. ( Необходимое условие существования экстремума)

Если точка x0 является точкой экстремума функции y f x , то в этой точке производная f x0 равна нулю или не существует.

Доказательство:

Пусть x0 – точка максимума. Тогда по определению точки экстремума f x f x0 x , где x0 x – точка, принадлежащая -окрестности точки

	x0 . Тогда,					f x0	x f x0
	1. При x 0	x 0 . Поэтому	f x		lim			0 .
							x
			0		x 0
	2. При x 0	x 0 . Поэтому	f x0		lim	f x0	x f x0	0 .
							x
					x 0

Это возможно только в двух случаях:

–оба предела равны между собой и равны нулю, т.е. f x0 0 .

–пределы различны, а значит f x0 не существует. Что и требова-

лось доказать.

Аналогично теорема 2 доказывается для случая, когда x0 – точка ми-

нимума.

Замечание. Утверждение обратное теореме 2 не всегда верно, т.е. если f x0 0 или f x0 – не существует, то это не всегда значит, что x0 – точ-

ка экстремума.

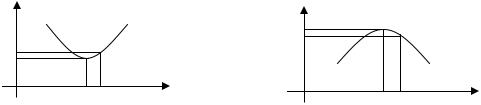
243

Пример. Для функции y x3

при x0 0

f x0 3x2

x

0 0 , но в этой

0

точке нет экстремума (см. рис. 2.14.5). А для функции y

3 x

при x 0 ,

1

0

f x0

x 0 – не существует, а экстремума также нет (см. рис. 2.14.6).

33 x2

0

y=x3

y

y 8

2

y

3 x

–8

–20 12

x

x

1

8

–8

рис. 2.14.6

рис. 2.14.5

Следовательно, точки экстремума относятся к критическим точкам, но не исчерпывают их, а являются только частью критических точек, которые поэтому называют подозрительными на экстремум.

Таким образом, теорема 2 действительно является лишь необходимым условием существования экстремума, но не достаточным, и его нельзя использовать для установления наличия экстремума функции в данной точке.

Теорема 3. ( Достаточное условие существования экстремума)

Если непрерывная функция y f x имеет производную в любой точке -окрестности точки x0 , кроме, быть может самой точки x0 и при переходе через x0 (слева направо) производная f x меняет знак с плюса на минус

(с минуса на плюс), то x0 – точка максимума (точка минимума).
Доказательство:					f x 0 при любом		x x0	; x0 и
Пусть		по условию теоремы
f x 0	при любом x x0; x0 . Тогда по теореме 1 функция							f x воз-
растает	на	интервале	x0 ; x0		и для всех	x из	этого	интервала
f x f	x0	, а на интервале		x0; x0 функция		f x	убывает, так что
f x f	x0	для всех	x из	этого	интервала, т.е.	f x	f x0	для всех

x x0 ; x0 , а значит по определению x0 – точка максимума. Ч. и т. д. Аналогично доказывается, что x0 – точка минимума.

В критических точках, где первая производная равна нулю, наличие экстремума можно установить по знаку второй производной.

Теорема 4. Если в точке x0 первая производная функции y f x равна нулю f x0 0 , а вторая производная в точке x0 существует и от-

				244
лична от нуля f x0 0 , то при				f x0 0 f x0 0				x0 – точка макси-
мума ( минимума).
Доказательство:
Пусть	f x0 0 . Так как, f x0 0 ( по условию), то								f x0 x
f x0 lim		f x0 x f x0		lim	f x0 x	0	, то			0 в
x 0		x		x 0	x				x
окрестности точки x0 .
Если x 0 , то f x0 x 0; если x 0 , то							f x0 x 0 . Следо-

вательно, при переходе через точку x0 первая производная меняет знак с минуса на плюс и тем самым x0 – точка минимума по теореме 3. Ч. и т. д.

Аналогично доказывается, что если f x0 0 , то x0 – точка максиму-

ма.

	Используя теоремы 1–3 рассмотрим алгоритм исследования функции
на монотонность и экстремумы.
	1. Найти область определения функции.
	2. Найти критические точки, подозрительные на экстремум, в которых
f x	x – не существует.

3.Убедиться, что критические точки принадлежат области определения функции (если это не так, то точки не являются точками экстремума).

4.Критическими точками разбить область определения функции на ин-

на каждом интервале.тервалы

5. По результатам исследования сделать вывод. Записать промежутки монотонности и найти экстремумы функции, если они есть.

Примеры. Исследовать функции на монотонность и экстремумы.

1. y x 2 2 x 3 3 . Проведем исследования по вышеприведенному

алгоритму.
1)	D y R .
2)	Чтобы найти критические точки решим уравнение f x 0 .
f x 2 x 2 x 3 3 3 x 3 2 x 2 2
x 2 x 3 2 2 x 3 3 x 2 x 2 x 3 2 5x.
x 2 x 3 2			5x 0 x						2, x 0,	x 3 – критические точки, подозри-
тельные на экстремум.							1		2	3
3)	Так как,			D y R , то x1, x2, x3 D y .
4)	+		–			+			+ x
	–2						3
				0

f 3 0 , f 1 0 , f 1 0 , f 4 0 .

					245
	5)	Согласно		теореме	1 функция возрастает на интервале
; 2 U 0;			и убывает на интервале 2;0 .
	По	теореме	3:	x1 2 –	точка максимума и max f x f 2 0 ;
x2 0	– точка минимума и min f x f 0 108 .

Точка x3 3 – не является точкой экстремума, так как не удовлетворяет теореме 3 (при переходе через эту точку производная не меняет знак).

2.y x 12 2

1)D y : x 2 2 0 D y ;2 U 2; .

2)f x x 22 3 ,

	f x	0	при любом x D y .
	f x	– не существует при x 2 3 0 x 2 – критическая точ-
ка, подозрительная на экстремум.
3)	x 2 D y x 2 – не является точкой экстремума (по опреде-
лению).
4)		+			–
					x
			–2

f0 0, f 3 0 .

5)Согласно теореме 1 функция возрастает на интервале ; 2 , а убывает на интервале 2; . Функция экстремумов не имеет.

2.14.3. Выпуклость и вогнутость графика функции. Точки перегиба

Теорема 5. Если функция y f x определена и непрерывна вместе со

своей производной	f x на интервале a;b и имеет внутри a;b конечную
вторую производную		f x . Тогда для выпуклости графика функции f x	в
a;b необходимо	и	достаточно, чтобы f x 0 , а для вогнутости	–
f x 0 .

Доказательство:

Докажем достаточное условие теоремы.

Пусть f x 0 для любой точки x a;b функции y f x и имеющую абсциссу x0 a;b касательную (см. рис. 2.14.7).

Запишем	уравнение
M x0; f x0 :	yкас f x0
y

yкас

y f(х0)

0

a

х0

b

	246
касательной			к	графику функции		в точке
f x0 x x0 , то				yкас f x0 f x0 x x0 .
	Тогда
	y yкас f x f x0 f x0 x x0 .
	По	теореме			Лагранжа	(п.2.12.3):
	f x f x0 f c x x0 , где					c x0; x .
	Поэтому,
	y yкас f c x x0 f x0 x x0 ,
x	y yкас		f c f x0 x x0 .

рис. 2.14.7	Разность f c f x0 преобразуем по тео-
f c f x0	реме Лагранжа:
	f c1 c x0 , где c1	x0;c .
Таким образом, y yкас f c1 c x0 x x0		.
Исследуем это равенство:

–если x x0 x x0 0, c x0 0 и f c1 0 . Следовательно, y yкас 0,

т.е. y yкас .

–если x x0 x x0 0, c x0 0 и f c1 0 . Следовательно, y yкас 0,

т.е. y yкас .

Итак, доказано, что во всех точках интервала a;b ордината касатель-

ной больше ординаты графика функции, т.е. касательная, проведенная к графику функции в любой точке с абсциссой из этого интервала расположена выше графика функции. А значит график функции выпуклый. Ч. и т. д.

Аналогично доказывается, что при f x 0 график функции вогну-

тый.				Определение. Точка графика функции, в
	y
				которой график функции меняет выпуклость на
				вогнутость или наоборот, называется точкой
				перегиба (см. рис. 2.14.8).
				В абсциссе точки перегиба вторая произ-
				водная или равна нулю, или не существует.
	а0	х0	b х	Пример. Функция y x3 при x 0 имеет
		рис. 2.14.8		точку перегиба (см. рис. 2.14.5). Действительно,
				вторая производная этой функции при x 0

247
равна нулю: y x 3x2 y x 6x x 0 0 . Функция	y 3 x также имеет

точку перегиба с абсциссой x 0 (см. рис. 2.14.6), в ней вторая производная

y		x	2		не существует.
			9 3 x5
				x 0

y

y=x4

16

Замечание. Обратное утверждение не всегда верно, т.е. если в точке x x0 вторая производная равна ну-

лю или не существует, то это не значит, что в точке с абсциссой x0 график функции будет иметь перегиб.

Пример. Для функции y x4 при x0 0 вторая

производная

обращается

в

ноль:

y 4x3 ,

-				x	y 12x2		x 0 0	. Однако для этой функции точки пере-
	2 0 1 2
рис. 2.14.9							0
					гиба нет (см. рис. 2.14.9).

Теорема 6. Если вторая производная f x при переходе через точку x0 , в которой она равна нулю или не существует, меняет знак, то точка графика функции с абсциссой x0 есть точка перегиба.

Доказательство:
Пусть f x 0 при	x x0 и	f x 0 при	x x0 , тогда, слева от

x x0 график функции выпуклый, а справа вогнутый. Следовательно, точка
x0; f x0 графика функции является точкой перегиба.	Ч. и т. д.
Аналогично доказывается, что если f x 0 при	x x0 и	f x 0
при x x0 , то точка x0; f x0 – точка перегиба.

Используя теоремы 5, 6 рассмотрим алгоритм исследования графика функции на выпуклость, вогнутость и на перегиб.

1)	Найти область определения функции.
2)	Найти точки, в которых f x 0 или	f x – не существует (точки,

подозрительные на перегиб).

3)Убедиться, что полученные точки принадлежат области определения функции (если это не так, то точки не являются абсциссами точек перегиба).

4)Точками, подозрительными на перегиб, разбить область определения

x на каж-

дом интервале.

5) По результатам исследования сделать вывод. Записать промежутки выпуклости, вогнутости. Если точки перегиба существуют, найти ординаты точек перегиба.

248

Пример. Найти точки перегиба функции y ln 1 x2 и исследовать

её график на выпуклость, вогнутость.

Решение:

Проведем исследование по выше приведенному алгоритму.

1)

D y R .

2)

Чтобы найти точки, подозрительные на перегиб, составим и решим

уравнение

x 0 :

2 x2 1 2x 2x

2x

2x2 2

f

x x2 1,

f

x

x2 1 2

x2 1 2 ,

f x 0 при

2x2

2 0 при x1

1, x2 1

f x существует при

любом x .

D y R , то x1,

x2 D y .

3)

Так как,

4)

-

+

-

-1

0

1

x

f 2 0 ,

f 0 0 ,

f 2 0 .

5)Согласно теореме 5 график функции выпуклый на интервале

; 1 U 1; , вогнутый – 1;1 .

По теореме 6 x1 1, x2 1 – абсциссы точек перегиба.

f 1 f 1 ln 2 , тогда M1 1;ln 2 и M2 1;ln 2 являются точками перегиба.

2.14.4 Наибольшее и наименьшее значения функции

По теореме 5 п.2.6.2: если функция y f x непрерывна на отрезкеa;b , то среди её значений на этом отрезке существует как наибольшее, так

и наименьшее значения.

Пусть функция y f x дифференцируема на интервале a;b , за ис-

ключением, может быть, конечного числа точек. Наибольшее и наименьшее значения функции y f x на отрезке a;b могут достигаться функцией

или в одной из критических точек, или на одном из концов отрезка a;b .

Алгоритм нахождения наибольшего (наименьшего) значения функции f x на отрезке a;b .

1) Найти критические точки функции y f x .