3. Минимизация функций алгебры логики

3.1. Некоторые понятия и определения

Под минимизацией понимается сокращение числа аргументов до минимума в заданном логическом выражении, не изменяя его значения. При синтезе схем дискретных устройств прежде всего необходимо получить логическое выражение, согласно которому должна работать электрическая схема заданного устройства. Если логическое выражение будет сложным, то электрическая схема, соответствующая этому выражению, будет содержать много элементов автоматики, а следовательно она будет дорогой и менее надежной.

Существующие методы синтеза дискретных устройств позволяют получать логические выражения, по которым должна строиться электрическая схема, только в самом сложном виде СДНФ. Минимизировать сложное логическое выражение можно путем использования законов и тождеств алгебры логики. Однако, такой путь минимизации логического выражения неэффективен.

Любой функции алгебры логики соответствует только одна СДНФ, а эта же ФАЛ может быть представлена несколькими ДНФ. Если ФАЛ может быть представлена несколькими ДНФ, то эти ДНФ называются тупиковыми. Тупиковые ДНФ могут содержать разное количество аргументов, поэтому из тупиковых ДНФ выбирается минимальная ДНФ (с минимальным количеством аргументов).

Таким образом процесс минимизации ФАЛ заключается в том, чтобы из СДНФ получить тупиковые ДНФ, а из тупиковых выбрать минимальную ДНФ. Разработаны и используются несколько методов минимизации ФАЛ как аналитических, так и табличных.

Наиболее распространенным методом минимизации функций алгебры логики, зависящих от пяти и более аргументов, является метод Квайна-Мак-Класски.

3.2. Аналитический метод минимизации фал

(Квайна-Мак-Класски)

В основу данного метода положен закон склеивания конституэнт единицы СДНФ. В результате склеивания конституэнт единицы получается сокращенная ДНФ. Сокращенной ДНФ называется такая ДНФ заданной функции, которая может содержать лишние слагаемые.

Пример 3.1. Найти сокращенную ДНФ следующего логического выражения заданного в СДНФ

Конституэнты единицы СДНФ представляют собой наборы аргументов, записанные в виде букв. Если аргумент равен нулю, то буква, соответствующая ему, имеет знак отрицания.

Алгоритм получения сокращенной ДНФ следующий:

1. Каждая конституэнта единицы, заданного логического выражения представляется двоичным числом.

2. Полученные двоичные числа разбиваются на группы по числу единиц и записываются в первый столбец в порядке возрастания числа единиц в группе.

3. Производится склеивание двоичных чисел первой группы с двоичными числами второй группы, двоичные числа второй группы с двоичными числами третей группы и т.д. Склеиваться будут только соседние двоичные числа. Два двоичных числа называются соседними, если они отличаются между собой только в одном разряде, например 110 и 100.

В результате склеивания получается сокращенное двоичное число (импликанта), где вместо аргумента, которым отличались два двоичных числа, ставится черточка. Сокращенные двоичные числа записываются во второй столбец и также делятся на группы по числу единиц. Склеенные двоичные числа первого столбца отмечаются выбранным знаком. Одно и то же число может склеиваться несколько раз, но отмечается только один раз.

Сокращенные двоичные числа второго столбца аналогично могут склеиваться между собой. В результате получаются сокращенные двоичные числа с двумя черточками и записываются в третий столбец и т.д.

Для склеивания двоичных чисел второго и последующих столбцов необходимо выполнение двух условий:

1. Чтобы склеиваемые числа были соседними.

2. Черточки в склеиваемых числах должны стоять в одинаковых разрядах.

Склеивание импликант (сокращенных двоичных чисел) продолжается до тех пор, пока выполняются эти два условия.

4. После прекращения процесса склеивания все сокращенные и не сокращенные двоичные числа всех столбцов, которые не отмечены знаком склеивания, рекомендуется обозначить латинскими буквами, сумма этих букв будет представлять собой сокращенную ДНФ. Повторно встречающиеся импликанты не рассматриваются.

Примечание.В процессе склеивания рекомендуется каждое двоичное число первого столбца обозначить его десятичным эквивалентом. Это необходимо для удобства при получении тупиковых ДНФ.

Решение примера 3.1. Выполняя вышеизложенный алгоритм получим:

Первый столбец			Второй столбец			Третий столбец
0.	0 0 0 0		0, 1	0 0 0 		0, 1, 2, 3	0 0 	A
1.	0 0 0 1		0, 2	0 0 0		0, 1, 8, 9	 0 0 	B
2.	0 0 1 0		0, 4	0 0 0		0, 2, 4, 6	0 0	C
4.	0 1 0 0		0, 8	 0 0 0		0, 4, 2, 6	0 0
8.	1 0 0 0		1, 3	0 0 1		0, 8, 1, 9	 0 0 
3.	0 0 1 1		1, 9	 0 0 1		1, 3, 9, 11	 0 1	D
6.	0 1 1 0		2, 3	0 0 1 		1, 9, 3, 11	 0 1
9.	1 0 0 1		2, 6	0 1 0		2, 3, 6, 7	0 1	E
7.	0 1 1 1		4, 6	0 1 0		2, 6, 3, 7	0 1
11.	1 0 1 1		8, 9	1 0 0 		3, 7, 11, 15	  1 1	F
15.	1 1 1 1		3, 7	0 1 1		3, 11, 7, 15	  1 1
			3, 11	 0 1 1	
			6, 7	0 1 1 	
			9, 11	1 0 1	
			7, 15	 1 1 1	
			11, 15	1 1 1	

Из результатов склеивания видно, что все числа первого и второго столбцов склеились. Не склеились только числа третьего столбца, из которых выбираем импликанты A,B,C,D,E,F, повторяющиеся отбрасываем. Таким образом, сокращенная ДНФ будет иметь вид

A  B  C  D  E  F = .

Все слагаемые сокращенной ДНФ называются простыми импликантами. Из сокращенной ДНФ можно получить тупиковые ДНФ, если они будут иметь место. Тупиковой ДНФ называется такая ДНФ ни одно слагаемое, из которой исключить нельзя, не изменяя ее значение.

Для получения тупиковых ДНФ необходимо построить импликантную таблицу, которая состоит из вертикальных и горизонтальных линий. Число вертикальных линий равно числу конституэнт единицы, которые содержаться в СДНФ заданного логического выражения. Число горизонтальных линий равно числу простых импликант сокращенной ДНФ. В рассмотренном примере 3.1. число конституэнт единицы равно 11 (0, 1, 2, 4, 8, 3, 6, 9, 7, 11, 15), а число простых импликант сокращенной ДНФ равно 6 (A,B,C,D,E,F). Импликантная таблица будет следующая

Таблица 3.1.

Импликантная таблица для примера 3.2

Простые импликанты получились в результате склеивания конституэнт единицы столбца 1. Например простая импликанта А получилась в результате склеивания четырех конституэнт единицы 0, 1, 2, 3 (см. столбец 3). В таблице 3.1. на пересечении горизонтальной линии импликанты А с вертикальными линиями конституэнт единицы 0, 1, 2, 3 стоят крестики, свидетельствующие о том, что импликанта А поглощает конституенты единицы 0, 1, 2, 3. Все остальные крестики в таблице 3.1. на пересечениях вертикальных и горизонтальных линий говорят о поглощении простыми импликантами соответствующих конституэнт единицы.

Для получения тупиковых ДНФ из таблицы 3.1. запишем следующее выражение

 = (A  B  C)(A  B  D)(A  C  E)CB(A  D  E  F)(C  E)(B  D)(E 

 F)  (D  F)F (3.1)

Выражение (3.1) представляет собой произведение сумм простых импликант, которые поглощают конституэнты единицы СДНФ. Для получения всех тупиковых ДНФ необходимо в выражении (3.1) раскрыть скобки. В результате получим сумму произведений простых импликант. Каждое полученное произведение по составу простых импликант будет представлять собой тупиковую ДНФ.

Раскрытие скобок выражения (3.1) представляет собой достаточно сложную процедуру, поэтому получить тупиковые ДНФ можно простым анализом импликантной таблицы и выражения (3.1). В выражении (3.1) в качестве отдельных сомножителей присутствуют импликанты B,C,F, которые обязательно должны войти в тупиковую ДНФ, т.к. конституэнта 4 (см. табл. 3.1.) поглощается только импликантой С, конституэнта 8 только импликантой В, а конституэнта 15 только импликантойF. Во все суммы простых импликант выражения (3.1) в качестве слагаемого входит хотя бы одна из импликантB,C,F. Следовательно, все конституэнты единицы будут поглощаться импликантамиB,C,F. Отсюда следует, что тупиковая ДНФ для заданной ФАЛ в примере 3.2. будет только одна

B  C  F=.

Эта тупиковая ДНФ одновременно будет и минимальной ДНФ.

Пример 3.2. Найти минимальную ДНФ следующего логического выражения

.

Решение

Первый столбец			Второй столбец
0.	0 0 0 0		0, 2	0 0 0	A
2.	0 0 1 0		0, 8	 0 0 0	B
8.	1 0 0 0		2, 6	0 1 0	C
6.	0 1 1 0		8, 9	1 0 0 	D
9.	1 0 0 1		6, 7	0 1 1 	E
7.	0 1 1 1		9, 13	1 0 1	F
13.	1 1 0 1		7, 15	 1 1 1	G
15.	1 1 1 1		13, 15	1 1 1	H

Произошло склеивание только соседних двоичных чисел первого столбца. Сокращенные двоичные числа второго столбца не склеиваются между собой. Следовательно, все они будут импликантами сокращенной ДНФ. Получили сокращенную ДНФ в следующем виде

A  B  C  D  E  F  G  H =000  000  010  100 

 011101111111 =

.

Для получения тупиковых ДНФ строится импликантная таблица

Т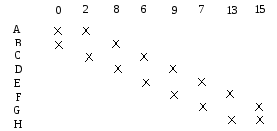аблица 3.2.

На основе импликантной таблицы 3.2., по аналогии с примером 3.1, запишем выражение

 = (A  B)(A  С)(В  D)(С  E)(D  F)(E  G)(F  H)(G  H).

Раскрыв скобки данного выражения получим

 = ABDEHABEFGABEFHACDEHACDFGADEHADGH

 ADEFGADEFHBCDEHBCDGHBCFGBCEFH.

Все полученные произведения по составу импликант являются тупиковыми ДНФ. Из полученных тупиковых ДНФ необходимо выбрать минимальную ДНФ. Так как все импликанты ABCDEFGHпо длине одинаковые, то минимальной ДНФ будет та тупиковая ДНФ, которая содержит наименьшее число импликант. Таких тупиковых ДНФ триADEH,ADGHиBCFH, которые состоят из четырех импликант. Любая из этих трех тупиковых будет минимальной.

Например BCFH=000010101111 =

= .