1) Ф_i – полином n-1 степени;

2) при x_i = x, Ф_i = 1;

3) при x = x_k, k  [1, n], k  i, Ф_i = 0.

Так как числитель

,

а знаменатель не равен нулю потому, что , ввиду условия и все x_i упорядочены по возрастанию;

4) как следствие свойств 2 и 3 L_n(x_i) = f(x_i), то есть в узле многочлен Лагранжа совпадает с приближаемой им функцией:

.

Для реализации многочлена Лагранжа удобно ввести функцию следующего вида:

При x = x_i и k  i выражение в квадратных скобках равно нулю, поэтому

.

Выражая L_n через и получим

При отладке программ целесообразно написать две процедуры-функции, с помощью которых выполняются расчеты: расчёт и

Используя эти процедуры, легко реализовать расчёт полинома Лагранжа.

Произведем оценку величины остаточного члена интерполяционного многочлена Лагранжа.

Допустим, что интерполируемая функция f(x) является гладкой, n раз дифференцируемой, тогда обозначим:

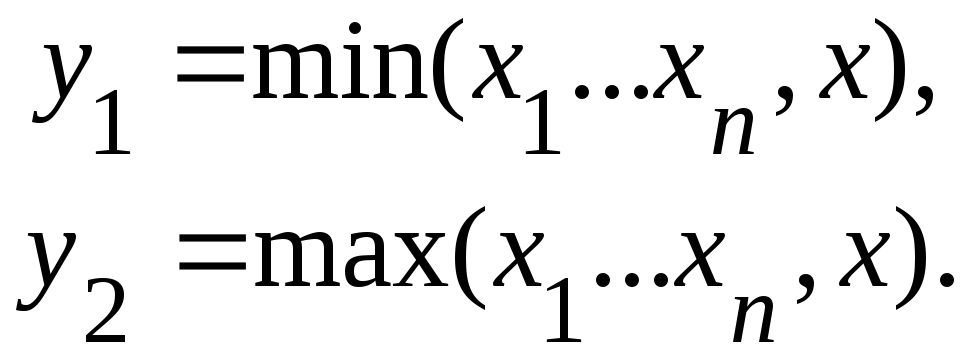
Тогда имеет место равенство [3]:

.

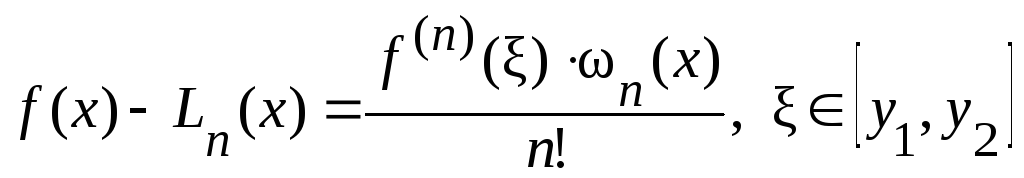3.2. Метод Ньютона

Рассмотрим систему

Определитель этой системы

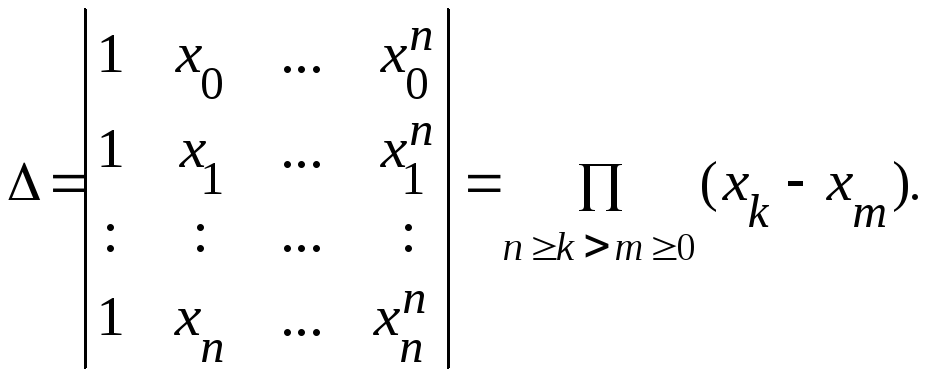(3.1)

Определитель (3.1) является определителем Вандермонда, и если значения в узлах различны, то в этом случае определитель не равен нулю, поэтому интерполяционный полином существует. Обозначается этот полином через P_n(x). Для определения P_n(x) введём понятие разделённой разности табулированной функции y(x).

Разделённые разности 1,2…n порядков дают приближённые значения производных соответствующих порядков.

Пусть P_n(x) – полином n-й степени, не содержащий кратных корней, тогда

,

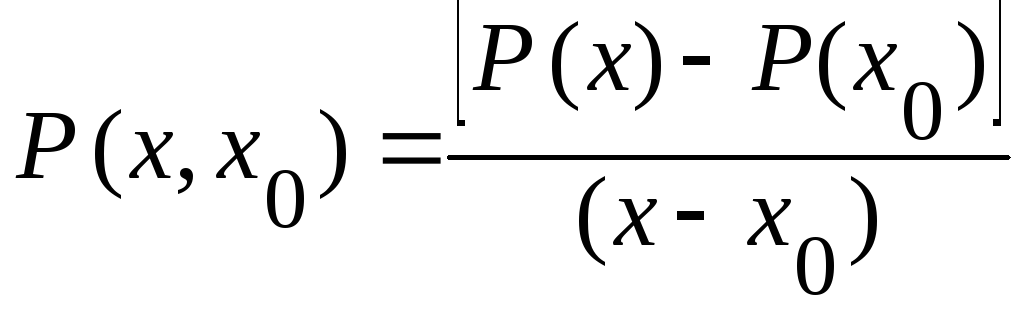полином (n-1)–й степени. Разность P(x) – P(x₀) при обращается в ноль, но P(x) – P(x₀) – полином, а поэтому по теореме Виета может быть представлен в виде

,

откуда следует утверждение о понижении порядка полинома P(x) на 1. Аналогично, вторая разность P(x, x₀, x₁) – полином степени n-2. Продолжая рассуждения, можно показать, что полином P(x, x₀…x_n-1) – полином нулевой степени, т.е. константа. Из вышеизложенного следует

Последовательно выражая P(x, x₀, x₁) через P(x, x₀, x₁, x₂), получим выражение для P(x):

.

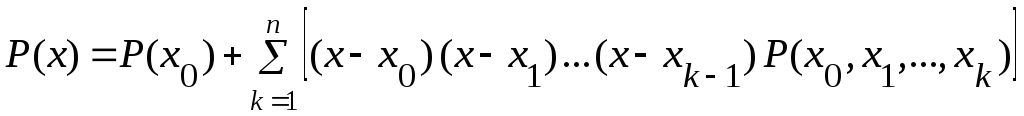Так как значения полинома P(x) в узлах x₀ … x_n равны значениям y₀ … y_n, тогда

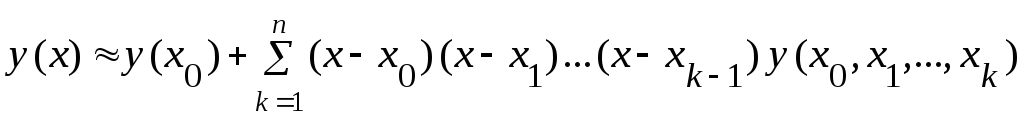. (3.2)

Для вычисления y(x₀, …, x_k) удобно воспользоваться табличной формой представления:

X0	Y(X0)
X1	Y(X1)	Y(X0, X1)	Y(X0, X1, X2)
X2	Y(X2)	Y(X1, X2)	Y(X1, X2, X3)	Y(X0, X1, X2, X3)
X3	Y(X3)	Y(X2, X3)

Примечание. За точностью удобно следить, оценивая скорость убывания разделённых разностей. Если они убывают медленно с возрастанием порядка, то хорошую точность, как правило, получить не удаётся. Для расчёта y(x) достаточно помнить информацию только верхней строки таблицы.

4. Решение нелинейных уравнений [2]

В случае уравнения с одним неизвестным задана непрерывная функция f(x) и требуется найти все или некоторые корни уравнения

f (x) = 0. (4.1)

Эта задача распадается на несколько задач:

1. Исследование количества, характера и расположения корней.

2. Поиск приближенного значения корней.

3. Выбор интересующих нас корней и вычисление их с требуемой точностью.

Первая и вторая задачи решаются аналитическими или графическими методами.

Например, многочлен имеет n корней, не обязательно различных, и все корни лежат внутри круга

Когда ищутся только действительные корни уравнения, то полезно составить таблицу значений f(x), если в двух соседних узлах лежит нечетное число корней уравнения (по меньшей мере один).

По таблице можно построить график функции y = f(x) и графически найти точки его пересечения с осью абсцисс. Этот способ дает неплохие приближенные значения корней. Приближенные значения корней уточняют различными итерационными методами.