6.1.2. Равномерное приближение.

Иногда ставится очень жесткое условие: во всех точках некоторого отрезка отклонение многочлена по абсолютной величине должно быть меньше заданной величины :

, .

При выполнении такого условия говорят, что многочлен равномерно аппроксимирует функцию с точностью на отрезке .

.

Определение. Абсолютным отклонением многочлена от функции на отрезке называется максимальное значение модуля разности между ними на данном отрезке:

(рис. 6.2а.) (6.5)

По аналогии вводится понятие среднеквадратичного отклонения при среднеквадратичном приближении функции

Рис. 6.2. К вопросу о приближениях: а – равномерное приближение, б – среднеквадратичное приближение.

Возможность построения многочлена, равномерно приближающего данную функцию, следует из теоремы Вейерштрасса об аппроксимации:

“Если функция непрерывна на отрезке , то для любого существует многочлен степени , абсолютное отклонение которого от функции на отрезке меньше ”.

В частности, если на отрезке разлагается в равномерно сходящийся степенной ряд, то в качестве аппроксимирующего многочлена можно взять частичную сумму этого ряда. (Такой подход широко используется, например, при вычислении на ЭВМ значений элементарных функций).

Имеется также понятие наилучшего приближения функции f(x) многочленом φ(x) фиксированной степени . В этом случае коэффициенты многочлена следует выбрать так, чтобы на заданном отрезке величина абсолютного отклонения (6.5) была минимальной.

В этом случае многочлен называется многочленом наилучшего равномерного приближения.

Существование и единственность многочлена наилучшего равномерного приближения вытекает из следующей теоремы:

Теорема. Для любой функции , непрерывной на замкнутом ограниченном множестве , и любого натурального существует многочлен степени не выше , абсолютное отклонение которого от функции минимально, т.е., причем такой многочлен единственный. Множество обычно представляет собой либо некоторый отрезок , либо конечную совокупность точек .

(Примером подобного разложения можно привести разложение элементарной функции в тригонометрический ряд. Мы знаем из соответствующего курса математического анализа, что наилучшим приближением функции в виде тригонометрического ряда

является ряд, где коэффициентами и являются коэффициенты Фурье).

6.2. Многочлены Тейлора.

Определение. Будем говорить, что ф-я принадлежит классу , и писать , если ф-ция (х) определена на отрезке и имеет на нем непрерывные производные до порядка включительно.

При вместо используют обозначение .

Запись означает, что ф-ция f(x) непрерывна на отрезке

В окрестности точки достаточно хорошее приближение ф-ции можно представить в виде многочлена Тейлора.

Пусть задана функция

Многочленом Тейлора степени ф-ции f(x) в точке называется многочлен . (6.6)

Многочлен (6.6) обладает тем свойством, что в точке он сам и все его производные до порядка включительно совпадают с соответствующими производными функции , т.е.

в чем легко убедиться, дифференцируя .

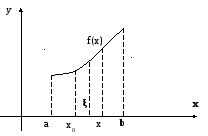
Рис.6.3. К приближению многочленом Тейлора.

Многочлен Тейлора хорошо приближает ф-цию в окрестностях точки . Погрешность, возникающая при замене функции ее многочленом , выражается остаточным членом формулы Тейлора в форме Лагранжа

, (6.7)

где - точка, лежащая строго между и при .

Так как по условию , то она ограничена на этом отрезке, т.е.

(6.8)

На основании (6.7) имеем

(6.9)

или , (6.10)

где .

Определение. Пусть - некоторая функция переменной с конечной областью определения на полуоси , причем может принимать сколь угодно малые значения. Тогда, если существуют такие положительные , что при всех , удовлетворяющих условию , выполняется неравенство

(6.11)

то пишут

(6.12)

и говорят, что есть O большое от (при ).

Согласно данному определению выполняются и следующие очевидные свойства. Если, и ,

причем области определения функций φ и ψ совпадают, т.е. D_φ= D_ψ , то

φ(h) + ψ(h), т.е. (6.13)

. (6.14)

Наконец, если, , то , где - постоянная, не зависящая от .

Определение. Аналогично, ф-ция , заданная для всех натуральных , есть O большое , если найдется такая постоянная , что при всех натуральных .

Возращаясь к остаточному члену ряда Тейлора, можем сказать, что погрешность приближения функции многочленом Тейлора есть , а неравенство (6.10) служит оценкой максимаьной погрешности на всем отрезке .

Из вышеприведенного очевидно, что погрешность аппроксимации многочленом Тейлора быстро убывает при и резко возрастает на концах . Причем особенно сильно - у наиболее удаленного от конца. Это есть основной недостаток использования ряда Тейлора при приближении функций.

Тем не менее, многочлены Тейлора широко используются на практике для приближения функций. Особенно это касается ф-ций, у которых легко находятся старшие производные, а остаточный член при . Прежде всего это функции , , , , , и другие.

Пример. Аппроксимировать функцию многочленом Тейлора на отрезке с абсолютной погрешностью, не превышающей .

Решение. Выбираем , т.е. в середине , с тем, чтобы минимизировать величину в составе оценки погрешности (6.10). Очевидно, что

, , , ,

.

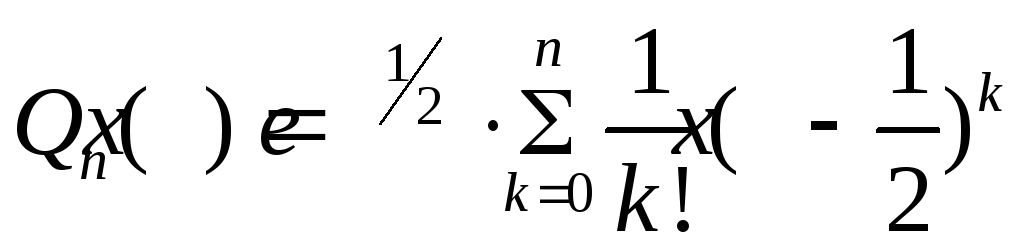Согласно (6.10) при и M_n+1 = e

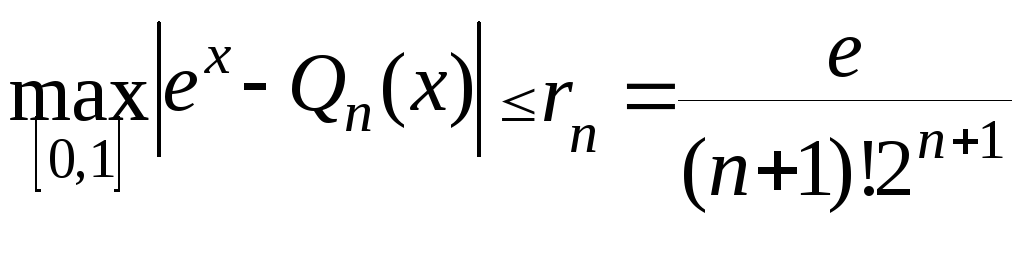
Для r_n составим таблицу:

n	3	4	5	6
rn	7,1·10^-3	7,1·10^-4	5,9·10^-5	4,3·10^-6

Видно, что .