Погрешность численного дифференцирования.

Аппроксимируем искомую функциюнекоторой приближенной функцией :

или . (12.7)

В качестве можно взять частичную сумму ряда (например, Тейлора) или

интерполяционную функцию. Тогда погрешность аппроксимации определяется остаточным членом ряда или интерполяционного многочлена.

Аппроксимированная функция может быть использована для

приближенного вычисления производной функции.

Дифференцируя равенство (12.7) последовательно можно найти значения

производных

В качестве приближенного значения производной порядка функции

можно принять соответствующее значение производной ф-ции , т.е.

.

Величина жедаёт нам погрешность аппроксимации

производной.

Для функции, заданной в виде таблицы с шагом эта погрешность зависит от , и ее записывают в виде

Показатель степени к называется порядком погрешности аппроксимации

производной (или просто порядком аппроксимации). При этом предполагается, что

значение по модулю меньше единицы.

Оценку погрешности посмотрим на примере приближения с помощью ряда

Тейлора.

Пусть функция задана в виде таблицы

Запишем ряд Тейлора для с точностью до членов порядка :

=.

Таким образом, .

Найдем производную в точке .

Данная формула совпадает с (12.3), и является аппроксимацией первого порядка, что видно по остаточному члену .

Используем этот же ряд Тейлора для оценки погрешности приближений

формулами (12.5) и (12.6).

Положив получаем .

Аналогично при имеем .

,

. (12.8)

Здесь, полагая, что - ограниченная величина,

можно написать .

Вычитая второе равенство из первого, получаем

,

, или

.

Видно, что получилось приближение второго порядка. Поэтому можно сказать, что приближение производной с помощью центральных разностей имеет более высокий порядок.

Складывая равенства (12.8), находим оценку погрешности приближения

производной второго порядка.

, или

.

Видим, что и эта аппроксимация имеет второй порядок.

Использование интерполяционных формул.

Пусть задана в виде таблицы с

постоянным шагом .

Запишем приближение функции с помощью интерполяционного

многочлена Ньютона.

… - безразмерная переменная.

Дифференцируя по , и помня, что

, можно

получить формулы для вычисления производных любого порядка.

Пример. Вычислить в точке х = 0.1 первую и вторую производные функции, заданной таблицей.

х	у
0	1.2833
		5274
0.1	1.8107		325
		5599		47
0.2	1.3606		372		2
		5971		49		0
0.3	2.9577		421		2
		6392		51
0.4	3.5969		472
		6864
0.5	4.2833

Здесь , Подставляя q в последние формулы, получим:

.

Мы видим, что интерполяционные многочлены Ньютона дают выражения для производных через разности . Но на практике проще выражать значения производных не через разности, а непосредственно через значения функции в узлах. Для получения таких формул удобно пользоваться формулой Лагранжа при постоянном шаге

Запишем интерполяционный многочлен Лагранжа и его остаточный член для случая трёх узлов интерполяции (n = 2) и найдем их производные:

Остаточный член полинома Лагранжа (см.6.26) имеет вид

.

Выше мы записывали остаточный член с использованием функции

.

Полагая, что , получаем:

.

При и, следовательно, при и, учитывая, что

, будем иметь:

. (12.8 а)

Так как во многих случаях трудно оценить, то при h малом приближенно полагают:

.

Следовательно, . (12.8 б)

Аналогично может быть найдена погрешность для второй производной

Остаточный член полинома Лагранжа (см.6.26) имеет вид

.

Так как здесь , то , где - значение производной третьего порядка в некоторой внутренней точке .

,

.

Сейчас мы можем найти значение производной в любом узле интерполяции

отрезка .

Запишем для наглядности последовательность вычисления производной

.

Проведя аналогичные вычисления, можно получить значения

:

Продолжая подобные вычисления для случая четырех узлов , получают следующие приближения производных:

,

,

(12.9)

,

.

В случае пяти узлов получают

,

,

, (12.10)

,

.

Из приведенных формул видим, что, используя значения функции в

узле, получаем приближения производных порядка.

Кроме того, обратим внимание на то, что при четных ( узлов)

наиболее простые выражения и наименьшие коэффициенты в остаточных членах получаются для производных в средних (центральных) узлах

и т. д.).

Для этих двух случаев формулы можно обобщить. Придадим номер

центральному узлу:

;

(12.11)

.

С помощью интерполяционных полиномов Лагранжа можно получить приближения и для старших производных. Приведем эти приближения.

В случае трех узлов интерполяции :

;

; (12.12)

.

В случае четырех узлов :

;

;

; (12.13)

.

В случае пяти узлов :

;

; ; (12.14)

;

.

Можно видеть, что приближение и вторых производных с помощью центральных разностей наиболее выгодны.

Улучшение аппроксимации.

Из соотношений для приближений производных очевидно, что порядок их точности прямо пропорционален числу узлов. Но с их увеличением эти соотношения становятся сложнее, объем вычислений возрастает.

Существует очень простой и эффективный способ уточнения решения при фиксированном числе узлов.

Это Метод Рунге-Ромберга.

Пусть -производная, которая подлежит аппроксимации; -конечно-разностное приближение этой производной на равномерной сетке с шагом ; -погрешность (остаточный член) аппроксимации, главный член которой можно записать в виде

.

Тогда выражение для приближения производной в общем случае можно представить в виде

. (12.15)

Запишем это же соотношение в той же точке при другом шаге .

Получим . (12.16)

Приравняем правые части последних равенств

;

;

.

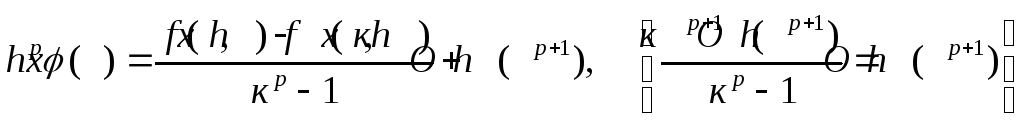Подставляя найденное выражение в равенство (12.15), получаем формулу Рунге:

. (12.17)

Эта формула позволяет по результатам двух расчетов значений производной

с шагами и порядками точности найти ее уточненное значение с порядком точности .

Пример. Вычислить производную функции в точке . (Для

оценки результатов вычислений мы заранее знаем точный ответ, так как ).

Пусть дана таблица значений ф-ции:

	0,8	0,9	1,0
	0,512	0,729	1,0

Найдем производную численно. (Из данных таблицы зависимость мы можем не знать).

Воспользуемся приближением производной с помощью левых разностей, имеющей первый порядок ().

Примем шаг равным 0,1. Потом - 0,2; т.е. .

;

.

По формуле Рунге находим уточненное значение производной:

.

Таким образом, мы убеждаемся, что формула Рунге дает более точное значение производной.

Предположим теперь, что расчеты м/б проведены с шагами Тогда уточненное решение для производной можно получить по формуле Ромберга, которая имеет вид

׃

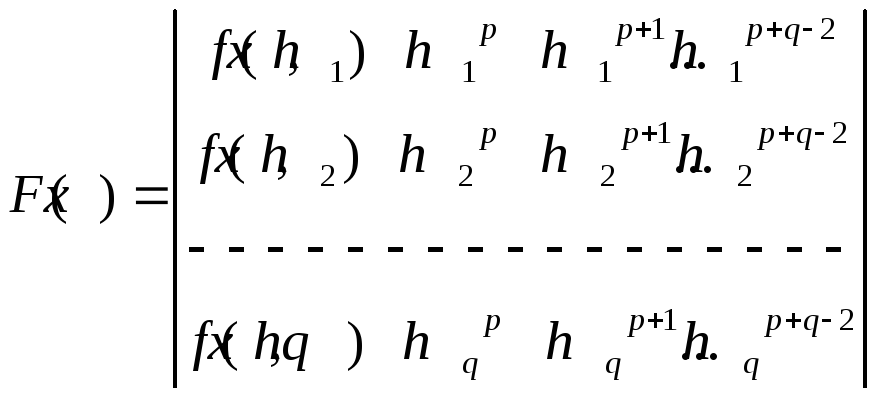Согласно последнему выражению порядок приближения возрастает на .