Применение метода Монте-Карло к вычислению определенных и кратных интегралов.)

1. Вычисление определённых интегралов.

а). Требуется вычислить интеграл .

Пусть х-равномерно распределенная случайная величина,

плотность распределения вероятности этой случайной величины:

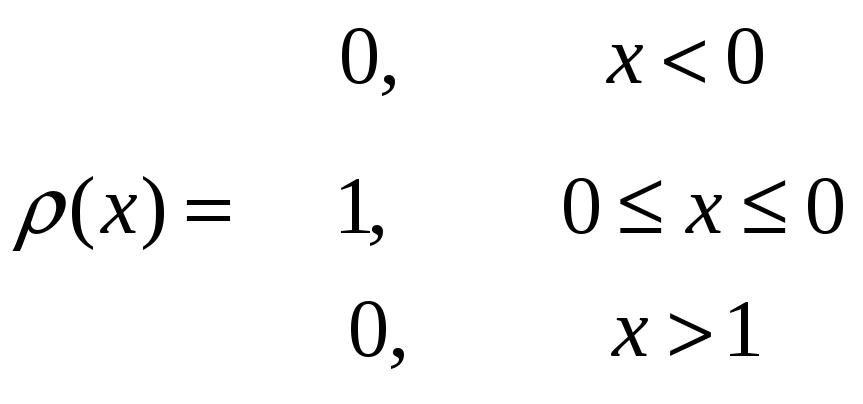
Согласно теории вероятностей математическое ожидание функции случайной величины определяется равенством

.

Поскольку , то имеем

. (13.27)

Приближенное значение математического ожидания можно найти, воспользовавшись формулой теоремы Чебышева

, (13.28)

где число испытаний, в каждом из которых получено значение случайной величины с равномерным распределением, Эти значения могут быть взяты из таблицы случайных величин (в ЭВМ есть программы генерации случайных величин с разными законами распределения). Из двух последних равенств следует формула вычисления определенного интеграла методом Монте-Карло

. (13.29)

----------------------------------------------------------

*) Данко П.Е., Попов А.Г., Кожевникова Т.Я.. Высшая математика в упражнениях и задачах. М. Высшая школа, 1980.

Пример: С помощью формулы (13.29) найти приближенное значение интеграла , взяв из таблицы случайных чисел подряд 30 значений и ограничиваясь тремя цифрами.

Решение. Расчетная таблица имеет следующий вид (для иллюстрации последовательности расчётов нет необходимости заполнять всю таблицу)

	1	2	3	4		29	30
	0,857	0,457	0,499	0,762		0,798	0,637
	0,734	0,209	0,249	0,581		0,637	0,012

Таким образом,

откуда по формуле (13.29) получаем

.

Точное значение интеграла равно

.

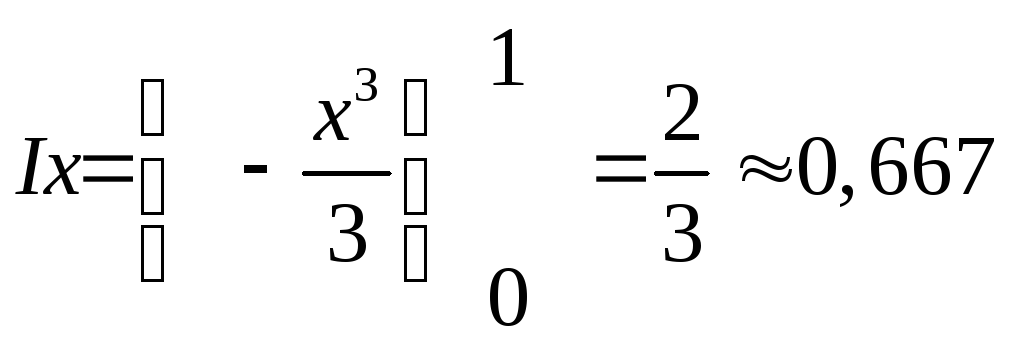Таким образом, абсолютная погрешность составила , а относительная погрешность .

б). Рассмотрим общий случай: пусть требуется вычислить .

С помощью равенства перейдем к новой переменной .

Тогда , (13.30)

где . Используя формулу (13.29) для приближенного вычисления интеграла в правой части равенства (13.30), получим

, (13.31)

где .

Расчетная таблица для вычисления определенного интеграла по формуле (13.31) имеет вид

3

1. Приближенное решение алгебраических и трансцендентных уравнений. Отделение корней.

В некоторых случаях при решении уравнений не удается аналитическим

путем найти точные решения.

Пусть дано уравнение , (14.1)

где определена и непрерывна на .

Определение. Всякое значение , обращающее функцию в нуль, т.е. такое, что , называется корнем уравнения (14.1) или нулем функции .

Приближенное нахождение изолированных действительных корней уравнения (14.1) обычно складывается из двух этапов:

1) отделение корней, т.е. установление малых промежутков , в которых содержится только один корень уравнения ;

1. уточнение приближенных корней, т.е. доведение их до заданной степени точности.

Для отделения корней полезна теорема:

Теорема. Если непрерывная функция принимает значения разных знаков на концах отрезка т.е. , то внутри этого отрезка содержится по меньшей мере один корень уравнения , т.е. найдется хотя бы одно число такое, что .

Последнее очевидно, если производная существует и сохраняет постоянный знак внутри интервала , т.е. если

.

Отделение корней начинается с установления знаков функции в граничных точках области ее существования.

Затем определяются знаки функции в ряде промежуточных точек

, выбор которых учитывает поведение функции на отрезке .

Если после нескольких операций нахождения окажется, что

то в силу теоремы 1 в интервале имеется корень уравнения .

Для отделения корней бывает достаточно провести процесс половинного деления, т.е. когда исследуемый интервал последовательно делится на 2, 4,… равных частей.

При этом каждый раз определяются знаки на концах интервалов.

Полезно помнить, что алгебраическое уравнение степени

имеет не более действительных корней. Поэтому, если для такого уравнения мы получили перемену знаков раз, то все корни его отделены.

Пример. Отделить корни уравнения . (14.2)

Решение. Составим таблицу

	-	-3	-1	0	1	3	+
	-	-	+	+	-	+	+

Из таблицы видно, что уравнение (14.2) имеет 3 действительных корня в интервалах (-3,-1), (0,1), (1,3).

Если существует непрерывная производная и корни уравнения легко находятся, то достаточно сравнить знаки функции в точках нулей производной и на концах отрезка .

Пример. Отделить корни уравнения (14.3).

Решение. Здесь , .

Имеем

	-	1	+
	+	-	+

Всего две смены знака (т.к. только одна точка экстремума).

В других точках не исследуем, поскольку в интервалах (-,1) и (1,+) не меняет знака - больше нет точек экстремума.

Видно, что в интервале (-,1) функция только убывает, в интервале (1,+)- только возрастает. Другие два оставшихся корня - комплексные.

Пример. Определить число действительных корней уравнения

. (14.4).

Решение. и . Видим, что функция только возрастающая, но имеется смена знака . Поэтому имеем всего один корень.