Вычисление значений рациональных дробей

Всякую рациональную дробь можно представить в виде отношения двух полиномов, т.е.

,

где ,

.

Если требуется определить значение R(x) в точке x = , то числитель и знаменатель дроби

можно найти, пользуясь схемой Горнера.

Приближенное нахождение сумм числовых рядов.

Пусть надо найти с заданной предельной абсолютной погрешностью  сумму S сходящегося ряда

Из сходимости ряда имеем

,

где S_n - n-я частичная сумма, R_n – остаток ряда, причем R_n  0 при n  .

Очевидно, что в поставленной задаче должно быть выполнено условие

.

В этом случае можно утверждать, что

На практике слагаемые а₁, а₂, , а_п определяются также приближенно. Кроме того, сумма S_n обычно округляется до заданного числа десятичных знаков.

Для учета всех этих погрешностей поступают так: выбирают три приближенных числа ₁, ₂ и ₃ такие, что

.

Число п членов ряда берут столь большим, чтобы остаточная погрешность удовлетворяла неравенству

.

Далее, каждое из слагаемых вычисляют с предельной абсолютной погрешностью . Тогда для суммы S_n справедливо неравенство

.

Наконец, полученный приближенный результат округляют до более простого числа с таким расчетом, чтобы погрешность округления была

.

В таком случае число является приближенным значением суммы S ряда с заданной погрешностью . Действительно, из приведенных выше неравенств имеем:

.

Чаще всего принимают

.

Если заключительное округление отсутствует, то обычно полагают

.

Для оценки остатка ряда полезны следующие теоремы.

Теорема 1. Если члены ряда представляют собой соответствующие значения положительной монотонно убывающей функции f(x), т.е. , то

0

1

2

Рисунок 5.1. Графическая иллюстрация к Теореме 1.

Теорема 2. Если ряд - знакочередующийся, т.е.

и модули его членов монотонно убывают, то

и

Пример. Найти сумму ряда

с точностью до 0,001.

Вспоминая, что

,

примем остаточную погрешность

.

Члены данного ряда представляют собой соответствующие значения монотонной функции.

.

Поэтому ;

; ; .

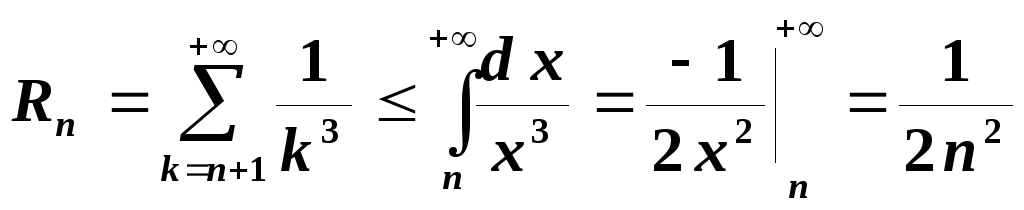Примем п = 45. Принимая предельную погрешность суммирования, равной ,

находим предельную абсолютную погрешность слагаемых а_k :

,

т.е. члены ряда а_k будем вычислять с пятью верными, в узком смысле, десятичными знаками после запятой. Опуская промежуточные вычисления, запишем, что в результате суммирования 45 членов, имеем

.

Округляя это значение до тысячных, имеем

.

Т.к. , то суммарная погрешность 

.

Т.о. .

Для сравнения: (с точностью до ).

Вычисление значений аналитической функции

Действительная функция f(x) называется аналитической в точке , если в некоторой окрестности этой точки функция разлагается в степенной ряд (ряд Тейлора):

(5.6)

Разложение f(x) в ряд Тейлора является удобным способом вычисления значений этой функции.

Если f() известно и требуется найти значение , где h – «малая поправка», то формулу (5.6) выгодно записывать в виде

(5.7),

где (0 < < 1) (5.8)

Подставляя значение h в (5.7), мы получаем задачу, решение которой подробно разбиралось выше (см. «нахождение сумм числовых рядов»).