Метод Монте-Карло для вычисления кратных интегралов
Особенно эффективно применение метода Монте-Карло для вычисления кратных интегралов. Например, двойной интеграл по области в виде единичного квадрата может быть представлен в виде
где
- это случайные числа, равномерно
распределённые на интервале
При интегрировании по прямоугольнику R, не совпадающему с единичным квадратом, необходимо сначала произвести преобразование переменных.
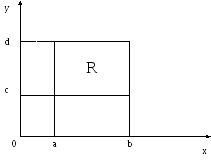
Обобщим метод
Монте-Карло на область произвольной
конфигурации. Пусть требуется вычислить
двойной интеграл по области
произвольной конфигурации.
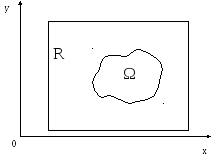
Построим прямоугольник
R
охватывающий область
и введём функцию,
совпадающую с
области
и равную нулю за пределами области
.
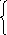
Очевидно, что искомый интеграл
Точность зависит от качества генератора, не совсем точная (равномерная плотность распределения).
Тема №7
Решение обыкновенных дифференциальных уравнений (оду)
К решению дифференциальных уравнений приводит большое число научно-исследовательских задач и задач инженерной практики, но лишь не многие из них удается решить аналитически, поэтому численные методы решения дифференциальных уравнений играют такую важную роль в инженерной практике.
Дифференциальные уравнения, содержащие одну независимую переменную и производные по ней, называются обыкновенными дифференциальными уравнениями.
Для решения дифференциального уравнения необходимо задание дополнительных условий, если дополнительные условия задаются при одном значении независимой переменной, то такие условия называются начальными, а задача решения уравнения называется задачей с начальными условиями или задача Коши.
Если условия задаются при двух или более значениях переменной, то такие условия называются граничными, а задачу называют краевой.
В задаче Коши роль
независимой переменной играет величина
(время), а дополнительное условие для
начального момента времени (
).
В краевых задачах в качестве независимой
переменной выступает координата отрезка,
а граничные условия задаются в начале
и конце отрезка.
Для решения задачи Коши и краевой принимают различные численные методы. Часто краевую задачу решают путем сведения её к задаче Коши. Отсюда следует, что обычно задачи Коши являются более легкими для численного решения.
При численном решении вводится шаг по координате, и решение находится в точках отстоящих друг от друга на величину шага. Для решения задачи Коши разработано множество методов, которые можно разделить на 2 группы:
1 группа – одношаговые методы.
В них для нахождения решения в следующей точке (удаленной на расстояние h) требуется информация лишь об одном предыдущем шаге.
2 группа – многошаговые методы.
Методы прогноза и коррекции.
В них для нахождения значения в следующей точке требуется информация из нескольких предыдущих точек.
При численном решении дифференциальных уравнений можно выделить 3 типа погрешности:
-
погрешность округления;
-
погрешность усечения, связана с аппроксимацией бесконечных рядов несколькими первыми членами, обусловлена численным методом;
-
погрешность распространения, она является результатом накопления погрешностей появившихся на предыдущих этапах счета.
Метод 28