Метод уточнения решения
Решение получается с помощью example.
……………………………
Решение полученные прямым методом содержат погрешности. В ряде случаев, особенно если объем системы велик эти погрешности могут быть значительными, рассмотрим итерационный процесс позволяющий уточнить решение на следующем итерационном шаге.
Пусть решается система
……………………………..
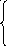
Пусть на k-ом итерационном шаге получено решение в виде ((x1)k,(x2)k, … , (xn)k)
Подставим полученное решение в левые части уравнений системы, результат вычислений этих уравнений обозначим (b1)k, (b2)k, … , (bn)k:
a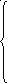
11
(x1)k+a12
(x2)k+a13
(x3)k+…+a1n
(xn)k=(b1)k
a21(x1)k +a22(x2)k +a23(x3)k +…+a2n(xn)k =(b2)k
a31(x1)k +a32(x2)k +a33(x3)k +…+a3n(xn)k =(b3)k
……………………………………………….
an1(x1)k +an2(x2)k +an3(x3)k +…+ann(xn)k =(bn)k
Вычтем из каждого уравнения первой системы соответствующее уравнений второй системы:
……………………………
–
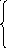
это не вязка для
уравнения с соответствующим номером.
П
олучается
система (x1)k+1
= (x1)k
+ e1
Это
соотношение уточняющее решение.
(xi)k+1 = (xi)k + ei
Преимуществом этого метода является то, что на каждом итерационном шаге решается система с одной и той же матрицей.
Метод №17
Метод Гаусса-Зейделя
Этот метод является одним из самых распространенных итерационных методов. Это связано с простотой метода. Перепишем уравнение системы, выразим х1 из первого уравнения, х2 из второго, из третьего – х3 и так далее. Получится система, которая имеет вид:
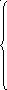
Для этого чтобы избежать проблем предварительно прежде записи системы необходимо производить перестановку таким образом, чтобы диагональные элементы не были равными нулю.
(х1)0, (х2)0, …, (хn)0 и на первом итерационном шаге с помощью первого уравнения находим (х11)\ = (b1-a12 (x2)0-…-a1n (xn)0) / a11, (x2)\ = (b2-a21 (x1)\ -…-a2n (xn)0) / a11,….
(x1)\, (x2)\, …, (xn)\, потом получаем второй итерационный шаг. Для сходимости итерационного процесса достаточно чтобы модули диагональных коэффициентов для каждого уравнения системы были не меньше суммы всех недиагональных элементов.
Тема5: Решение систем нелинейных уравнений
Метод18
Простой итеррации
Пусть требуется найти решение системы из n уравнений с t неизвестными.
…………………..
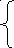
В общем случае прямых решений систем нелинейных уравнений нет.
Метод простой итерации. Преобразуем исходную систему.
…………………..
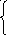
Это можно сделать всегда, причем различными способами.
Задается начальное приближение. (x1)0,…,(xn)0. Из первого уравнения находим
(x1)\ =f1((x1)0 , (x2)0, …,(xn)0)
Из второго уравнения находим:
х2=f2((x1)2, (x2)0, …,(xn)0)
При использовании метода простой итерации успех во многом зависит от удачного выбора приближения, чем больше вероятность того, что метод будет расходиться. Для системы существует область сходимости, если начальное приближение попадает в эту область, то итерационный процесс будет сходиться. Чем больше число неизвестных, тем меньше число сходимости.
Метод 19