Сплайны третьей степени

На практике широкое распространение получили сплайны третьей степени, имеющие на всем интервале (a,b) первую и вторую производные эти сплайны называются кубическими. На первом частичном отрезке сплайн можно представить в виде полинома.

- условие непрерывности для каждого узла;

- условие непрерывности для первой производной;

- условие непрерывности для второй производной.

В результате образуется система линейных уравнений, решая которую можно найти коэффициенты сплайна

Метод №4

Метод наименьших квадратов

Полином Лагранжа и сплайн в точности проходят через точки {x_i,y_i} такой подход, при построении (аппроксимации) не всегда оправданы, дело в том, что данные {x_i,y_i} полученные экспериментально имеют определенную погрешность, поэтому аппроксимируемая зависимость не обязана с точностью проходить через экспериментальные точки, а только по возможной близости к ним. Пусть аппроксимируемая зависимость имеет вид y = f(x) следовательно, ∆y = y_i - f(x_i), величина характеризует отклонение экспериментальных данных от аппроксимирующей зависимости эта величина положительна и отрицательна, что делает ее неудобно в качестве меры близости. Удобней использовать квадрат этой величины. Для того, чтобы аппроксимирующая функция была по возможности близкой ко всем экспериментальным точкам эта величина должна быть S = ∑(y_i – f(x_i))² минимальной. Метод, имеющий значение минимума и называется методом наименьших квадратов. Обычно аппроксимирующую зависимость выбирают из некоторого класса функций зависящих от определенного числа параметров y = f(a,b,c,…,x). Параметры a b c подбирают таким образом, чтобы обеспечить минимум значение S = ∑(y_i – f(x_i))². Используя значение минимума для функции, зависящей от нескольких переменных получим систему уравнений для нахождения параметров a,b,c…

…..

Мы получили систему, число уравнений которой равно числу параметров.

Наиболее часто экспериментальные функции аппроксимируют линейной функцией, в этом случае

Перепишем полученную систему:

a (∑x²_i) + b(∑x_i) = ∑y_i x_i

a (∑x_i) + bn = ∑y_i

Получили систему уравнений с двумя неизвестными a и b

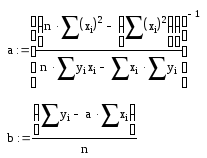
Аналогичным образом можно получить аппроксимирующую зависимость в виде полинома y = a₀+a₁x+a₂x²+…+a_mx^m, где m ≤ n – 1

Метод наименьших квадратов можно использовать так же при получении нелинейных двух параметрических аппроксимирующих зависимостей. Вид аппроксимирующих зависимостей может быть заранее известен по некоторым физическим соображениям. Часто физическая зависимость имеет экспоненциальный вид y = be^ax.

Эту зависимость можно привести к линейной: lny = ax + lnb: Y = AX + B

Используя экспериментальны данные мы строим экспоненциальные данные следующим образом:

{x_i,y_i} = {X_i,Y_i} = {x_i,lny_i}

AB = (a,b), a = A, b = e^B

Построим таблицу позволяющую получать нелинейные аппроксимирующие зависимости:

№ метода	y = f(x)	X	Y	a	B
5	y = ax^2+b	x^2	y	A	B
6	y = 1/ax +b	x	1/y	A	B
7	y = ax +b	x	x/y	A	B
8	y = be^ax	x	lny	A	e^B
9	y = be^a/x	1/x	lny	A	e^B