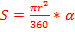-
Признаки равнобедренной трапеции: 1) если углы при основании равны; 2) если диагонали равны.
-
Свойства равнобедренной трапеции: 1) углы при основании и боковые стороны равны; 2) диагонали равны.
-
Прямоугольник — параллелограмм, у которого все углы прямые.
-
Свойство прямоугольника: диагонали прямоугольника равны.
-
Признаки прямоугольника: 1) если в параллелограмме диагонали равны; 2) если в параллелограмме угол равен 90°
-
Ромб — параллелограмм, у которого все стороны равны.
-
Свойство ромба: его диагонали лежат на биссектрисах углов и они взаимно перпендикулярны.
-
Признаки ромба: 1) Если диагональ параллелограмма является биссектрисой его угла, то параллелограмм — ромб. Если диагонали параллелограмма перпендикулярны, то параллелограмм — ромб.
-
Квадрат — прямоугольник, у которого все стороны равны.
-
Свойства квадрата: 1) все его углы прямые; 2) диагонали равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
-
Площадь фигуры — число, которое показывает, сколько единичных квадратов содержится в фигуре.
-
1)Равные многоугольники имеют равную площадь. 2) Площадь квадрата равна квадрату его стороны. 3)Если многоугольника составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
-
Площадь параллелограмма равна произведению его основания на высоту.
-
Площадь треугольника равна половине произведения его основания на высоту. Площадь прямоугольного треугольника равна половине произведения его катетов.
-
Площадь трапеции равна произведению полусуммы его оснований на высоту.
-
Площадь ромба равна половине произведения его диагоналей.
-
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
-
Теорема Пифагора. В прямоугольном △ квадрат гипотенузы равен сумме квадратов катетов.
-
Теорема обратная теореме Пифагора. Если квадрат одной стороны △ равен сумме квадратов двух других сторон, то треугольник прямоугольный.
-
Подобные треугольники — треугольники, у которых углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам второго.
-
Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
-
Отношение периметров двух подобных треугольников равно коэффициенту подобия. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
-
Первый признак подобия △: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
-
Второй признак подобия △: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами равны, то такие треугольники подобны.
-
Третий признак подобия △: если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.
-
Расширенная теорема Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
-
Средняя линия треугольника — отрезок, соединяющий середины двух его сторон.
-
Свойство средней линии треугольника: средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
-
Средняя линия трапеции — отрезок, соединяющий середины ее боковых сторон.
-
Свойство средней линии трапеции: средняя линия параллельна основаниям и равна их полусумме.
-
Среднее пропорциональное между двумя отрезками — отрезок XY называется среднем пропорциональным для отрезков AB и CD, если XY =
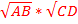
-
Первая теорема о среднем пропорциональном: высота прямоугольного △, проведённая из вершины прямого угла есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
-
Вторая теорема о среднем пропорциональном: катет прямоугольного △ есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключённого между катетом и высотой, провёденной из вершины прямого угла.
-
sin острого угла в прямоугольном треугольнике — отношение противолежащего катета к гипотенузе. cos острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе.
-
tg острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему. ctg острого угла в прямоугольном треугольнике — отношение прилежащего к противолежащему.
-
Окружность — геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
-
Касательная к окружности — прямая, имеющая с окружностью только одну общую точку.
-
Свойство касательной — касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
-
Признак касательной: если прямая проходит через конец радиуса, лежащего на окружности, и перпендикулярна к этому радиусу, то она является касательной.
-
Центральный угол — это угол с вершиной в центре окружности. Вписанный угол — это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
-
Теорема о вписанном угле: вписанный угол измеряется половиной дуги, на которую он опирается. Теорема о центральном угле: градусная мера дуги окружности равна градусной мере центрального угла, который на нее опирается.
-
Следствие из теоремы о вписанном угле: вписанные углы, опирающиеся на одну и ту же дугу, равны. Угол, опирающийся на диаметр окружности — прямой.
-
Теорема о пересекающихся хордах окружности: если две хорды окружности пересекаются, то произведения отрезков одной хорды равно произведению отрезков другой хорды.
-
Свойство биссектрисы угла: каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон, то есть равноудалена от прямых, содержащих стороны угла. Каждая точка, лежащая внутри угла и равноудалённая от сторон угла лежит на его биссектрисе.
-
Серединный перпендикуляр к отрезку — прямая, проходящая через середину данного отрезка и перпендикулярная к нему.
-
Каждая точка срединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Каждая точка равноудаленная от концов отрезка лежит на срединном перпендикуляре к нему.
-
Медианы треугольника пересекаются в одной точке.
-
Биссектрисы треугольника пересекаются в одной точке.
-
Высоты треугольника или их продолжения пересекаются в одной точке.
-
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
-
Вписанная в многоугольник окружность — окружность, которая касается всех сторон данного многоугольника.
-
Описанная около многоугольника окружность — это окружность, которая содержит все вершины данного многоугольника.
-
Теорема об описанной окружности: около любого треугольника можно описать окружность, и причём только одну. Центр такой окружности находится в точке пересечения серединных перпендикуляров к сторонам треугольника. Теорема о вписанной окружности: в любой треугольник можно вписать окружность, и причём только одну. Центр такой окружности находится в точке пересечения биссектрис данного треугольника.
-
В описанном четырёхугольнике суммы длин противоположных сторон равны. Если в выпуклом четырёхугольнике суммы длин противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.
-
В любом вписанном четырёхугольнике сумма противоположных углов равна 180˚. Если в выпуклом четырёхугольнике сумма противоположных углов равна 180˚, то около этого четырёхугольника можно описать окружность.
-
У любого четырёхугольника, вписанного в окружность, суммы пар противоположных углов равны 180о. В четырёхугольник можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны.
-
У любого четырёхугольника, вписанного в окружность, суммы пар противоположных углов равны 180о. Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равны 180 градусам.
-
Формула Геронагде S — площадь, p — полупериметр, а,b,c — стороны и
 .
.
9 Класс
-
Вектор — направленный отрезок, для которого определенно, какой из его концов — начало, а какой — конец. Модуль ненулевого вектора — длина отрезка, задающего этот вектор.
-
Коллинеарные векторы — векторы, которые либо лежат на одной прямой, либо на параллельных прямых. Коллинеарные векторы делятся на сонаправленные и противоположнонаправленные.
-
Равные векторы — векторы, у которых равны модули и они сонаправлены.
-
Теорема об откладывании вектора от точки: от любой точки на плоскости можно отложить вектор, равный данному вектору
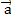 ,
и притом только один.
,
и притом только один. -
Правило треугольника: Пусть
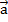 и
и 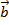 — два вектора. Отметим произвольную
точку А и отложим от нее вектор
— два вектора. Отметим произвольную
точку А и отложим от нее вектор 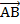 ,
равный
,
равный 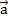 .
Затем от точки В отложим вектор
.
Затем от точки В отложим вектор 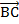 ,
равный
,
равный 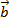 .
Вектор
.
Вектор 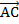 — сумма векторов
— сумма векторов 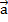 и
и 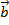 .
. -
Правило параллелограмма (сложение двух неколлинеарных векторов): чтобы сложить неколлинеарные векторы
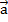 и
и 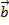 ,
нужно отложить от какой-нибудь точки
A
на плоскости векторы
,
нужно отложить от какой-нибудь точки
A
на плоскости векторы 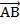 =
= 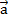 и
и 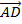 =
= 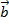 и построить параллелограмм ABCD.
и построить параллелограмм ABCD.
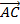 =
= 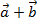 .
. -
Законы сложения векторов: 1) переместительный:
 =
= 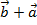 ;
2) сочетательный:
;
2) сочетательный: 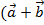 )
+
)
+ 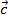 =
=  +
+  ).
). -
Вектор, противоположный данному — вектор, длина которого равна длине данного и ему противоположнонаправленный.
-
Разность векторов
 и
и 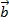 — такой вектор
— такой вектор 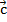 ,
что
,
что 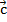
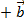 =
= 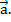
-
Свойство разности:
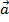 —
— 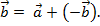
-
Первый способ вычитания векторов: откладывают на плоскости вектора от одной точки, соединяют концы этих векторов. Началом вектора разности будет конец вектора в вычитаемом, а концом вектора разности будет конец вектора в уменьшаемом.
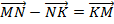
-
Второй способ: к первому вектору прибавить вектор противоположный данному.
![]() +(-
+(-![]()
-
Законы произведения вектора на число: 1) сочетательный: k,l — числа. (kl)
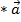 =
= 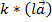 ;
2) 1-ый распределительный: (k+l)
;
2) 1-ый распределительный: (k+l)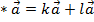 ;
3) 2-ой распределительный:
;
3) 2-ой распределительный: 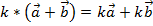 .
. -
Лемма: если векторы
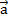 и
и 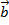 коллинеарны и
коллинеарны и 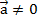 ,
то существует такое k,
что
,
то существует такое k,
что
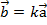
-
Любой вектор в ПСК можно разложить по двум неколлинеарным векторам, причём это разложение единственно
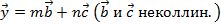
-
Координатные векторы — векторы
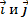 ,
длины которых равны единице. Направление
,
длины которых равны единице. Направление
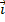 совпадает с направлением OX,
а направление
совпадает с направлением OX,
а направление 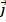 — с OY.
— с OY. -
Координаты вектора — коэффициенты разложения вектора по координатным векторам
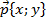 .
Равные векторы имеют равные координаты.
.
Равные векторы имеют равные координаты. -
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на число. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
-
Каждая координата вектора равна разности соответствующих координат его конца и начала.
-
Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
-
Вычисление длины вектора по его координатам. Длина вектора
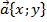 выясняется так:
выясняется так: 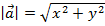 .
. -
Расстояние между двумя точками в координатах.
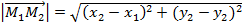
-
Уравнение окружности:
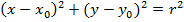 .
Частный вид — окружность с центром в
начале координат C(0;0):
.
Частный вид — окружность с центром в
начале координат C(0;0):
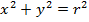
-
Уравнение прямой: ax+by+c=0.
Частные
случаи: 1) ![]() -
уравнение прямой, параллельной OX
(
-
уравнение прямой, параллельной OX
(![]() -число!);
2)
-число!);
2)![]() — уравнение прямой, параллельной OY
(
— уравнение прямой, параллельной OY
(![]() -число!);
3) уравнение оси OY
х=0, уравнение OX
у=0.
-число!);
3) уравнение оси OY
х=0, уравнение OX
у=0.
-
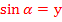 ;
;
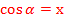 (при
(при 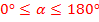 );
);
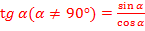
-
Координаты точки равны соответствующим координатам радиус-вектора.
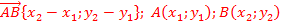 .
. -
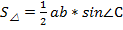 .
Площадь
.
Площадь 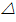 равна половине произведения двух его
сторон на синус угла между ними.
равна половине произведения двух его
сторон на синус угла между ними. -
Расширенная теорема синусов.
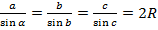 .
Стороны треугольника пропорциональны
синусам противолежащих углов.
.
Стороны треугольника пропорциональны
синусам противолежащих углов. -
Теорема косинусов:
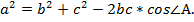 Квадрат стороны треугольника равен
сумме квадратов двух других сторон
минус удвоенное произведение этих
сторон на косинус угла между ними.
Квадрат стороны треугольника равен
сумме квадратов двух других сторон
минус удвоенное произведение этих
сторон на косинус угла между ними. -
Решение треугольника по двум сторона и углу между ними. Дано: a, b, ∠ C. Hайти: c, ∠A, ∠B.
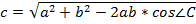 ;
;
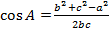 ;
∠
B=180°-
∠
A
- ∠
C.
;
∠
B=180°-
∠
A
- ∠
C. -
Решение треугольников по стороне и прилежащим к ней углам. Дано: a, ∠ B, ∠ C. Найти: ∠ A, b, c. ∠ A = 180°- ∠ B - ∠ C;
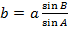 ;
;
 .
. -
Решение треугольника по трем сторонам. Дано: a, b, c. Найти: ∠ A, ∠ B, ∠ C.
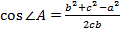 ;
;
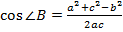 ;
∠
C=180°-
∠
B
- ∠
A.
;
∠
C=180°-
∠
B
- ∠
A. -
Скалярным произведением векторов
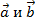 называется произведение длин этих
векторов на косинус угла между ними.
называется произведение длин этих
векторов на косинус угла между ними.
 .
. -
Скалярное произведение векторов
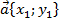 и
и 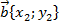 выражается формулой
выражается формулой 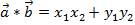 .
. -
Векторы перпендикулярны, когда скалярное произведение ненулевых векторов равно нулю.
-
Законы скалярного произведения: 1) сочетательный:
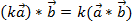 ;
2)распределительный:
;
2)распределительный: 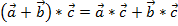 ;
3) переместительный:
;
3) переместительный: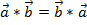 .
Свойство:
.
Свойство: 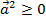 ,
причем
,
причем
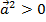 при
при
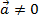 .
.
-
Правильный многоугольник — выпуклый многоугольник, у которого все углы и стороны равны.
-
Около любого правильного многоугольника можно описать окружность, и притом только одну.
В любой правильный многоугольник можно вписать окружность, и притом только одну.
-
Площадь правильного многоугольника
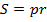 ;
;

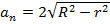 ;
;
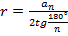 /
/ 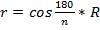 .
. -
Для правильного
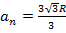 ;
для правильного четырёхугольника
;
для правильного четырёхугольника 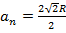 ;
;
для
правильного шестиугольника![]()
-
Дуга окружности — часть окружности, ограниченная двумя точками. Круг — часть плоскости, ограниченная окружностью.
-
Сектор — часть круга, ограниченная двумя радиусами. Сегмент — плоская фигура, часть круга, ограниченная дугой окружности и её хордой или секущей.
-
Длина окружности:
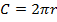 ;
длина дуги:
;
длина дуги: 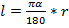 или
или 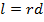 ;
Площадь круга:
;
Площадь круга: 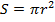 .
. -
Площадь сектора: