1.11.Автоматическое регулирование перетоков мощности

При максимальной загрузке межсистемных и внутрисистемных ЛЭП (транзитов) их надежная работа обеспечивается с помощью устройств автоматического регулирования перетоков активной мощности (АРПМ).

Наилучшие результаты достигаются при так называемом балансирующем действии АРПМ.

Рис. 1 12. Принцип балансирующего действия АРПМ на межсистемной линии электропередачи.

Если переток мощности, направленный из энергосистемы I в энергосистему II, превышает уставку устройства АРПМ, последнее воздействует одновременно на уменьшение мощности электростанций энергосистемы I и увеличение мощности электростанций энергосистемы II. При таком действии АРПМ частота в ЭЭС остается неизменной, а следовательно, остаются неизменным перетоки мощности по другим ЛЭП.

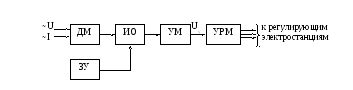
Рис. 1.13. Структурная схема АРПМ.

Основным органом устройства АРПМ является измерительный орган ИО, который подключен к датчику мощности ДМ. Измерительный орган ИО сопоставляет фактическую мощность, передаваемую по ЛЭП, с уставкой, задаваемую устройством ЗУ, и создает на своем выходе напряжение, которое пропорционально отклонению перетока мощности, а знак соответствует знаку отклонения. Выходное напряжение обычно усиливается усилителем мощности УМ.

Регулятор перетока АРПМ возвращает переток мощности к заданной уставке при его отклонении от уставки как в сторону увеличения, так и в сторону уменьшения. Однако в ряде случаев имеется необходимость регулировать переток мощности только в сторону уменьшения, т.е. ограничивать его максимальное значение. В этих случаях АРПМ выполняется для работы в режиме ограничения и соответственно называется автоматическим ограничителем перетока мощности (АОПМ). Автоматическое ограничение перетока мощности обычно осуществляется с большим быстродействием, чем регулирование перетока.

1.12. Математическая формулировка задачи оптимизации режима ээс

Математически можно сформулировать задачу оптимизации следующим образом. Имеется функция n переменных – F(x₁, x ₂, ..., x _n). Эти переменные связаны между собой k уравнениями или неравенствами связи:

(1.14)

где W₁, W₂, ..., W_k - некоторые функции переменных x_i (i = 1,2,...n).

Требуется найти минимум функции F.

Решение задачи оптимизации при ограничениях в форме неравенств требует применения весьма сложных методов оптимизации (метод Куна-Таккера и др.). Будем рассматривать более простые методы оптимизации при ограничениях переменных в форме уравнений. В этом случае число уравнений k должно быть меньше n.

1.13. Метод Лагранжа

При решении задач оптимизации режима широко применяется метод неопределенных множителей Лагранжа. При этом вместо условий экстремума функции F(х₁, х₂, ...х_n) n переменных, связанных между собой k соотношениями (1.14), ищут условия экстремума функции Лагранжа

(1.15)

где _i (i=1,2,...k) – постоянные множители, определяемые при отыскании функции F. Эти множители называются неопределенными множителями Лагранжа.

Приравняв нулю, частные производные от S по всем n переменным функциям, получим следующие n уравнений:

(1.16)

Из n уравнений (1.16) и k уравнений связи (1.14) составим всего (n+k) уравнений. Число неизвестных также равно (n+k), а именно: n искомых значений переменных - х₁, х₂,...х_n - и k множителей Лагранжа - ₁, ₂, ..._k.

Это дает возможность найти аргументы, соответствующие экстремуму функции S. Но эти же значения, как известно, характеризуют и экстремум минимизируемой функции F.

В рассмотренном методе определялись аргументы, соответствующие экстремуму минимизируемой функции F. Чтобы найденный экстремум действительно был бы минимумом, необходимо проверить знак второго дифференциала функций F или S. Если d²F  0 или d²S  0, то данный экстремум является минимумом.

Определение знака d²F или d²S очень сложно. На основании опыта исходят из ряда допущений, позволяющих считать, что найденный экстремум является минимумом.

В качестве примеров применения метода Лагранжа рассмотрим ряд упрощенных задач по оптимизации распределения мощностей.

1. При неучете влияния изменений потерь в сетях Р и суммарных нагрузок узловых точек Р_н оптимальное распределение активной мощности может быть найдено следующим образом.

Обозначим суммарные затраты, минимум которых соответствует оптимальному режиму, через Т. Искомыми переменными являются значения активной мощности отдельных агрегатов (или станций) Р₁, Р₂, ...Р_n, где n - число агрегатов (или станций).

Допустим, что суммарные затраты зависят только от величины активных мощностей, т.е.:

Т = f (Р₁, Р₂, ..., Р_n) (1.17)

Далее считаем, что станции – ТЭС.

Искомые переменные связаны одним уравнением баланса активных мощностей:

W = Р₁ + Р₂ + ... + Р_n - Р_н - Р = 0, (1.18)

где по допущению Р_н = const и Р = const.

При этом функция Лагранжа

S = T + W (1.19)

Условия экстремума соответствуют равенству нулю частных производных от S по всем n переменным:

(1.20)

Уравнения (1.20) можно записать иначе:

(1.21)

Т.к. суммарные затраты равны сумме затрат по каждому из агрегатов, т.е.

Т = Т₁ + Т₂ +...+ Тn,

то

. (1.22)

Частная производная от затрат на каком-либо агрегате по активной мощности агрегата называется удельным приростом затрат агрегата и обозначается буквой . Она зависит от величины активной мощности:

(1.23)

При этом условия оптимального распределения активных мощностей записываются следующим образом:

₁ = ₂ = ... = _n;

(1.24)

Р₁ + Р₂ + ... + Р_n = Р_н + Р.

Уравнения (1.24) определяют оптимальные значения Р₁, Р₂, ..., Р_n активных мощностей отдельных агрегатов. Таким образом, при неучете изменений суммарной нагрузки узловых точек и потерь в сетях условием оптимального распределения активных мощностей является принцип равенства удельных приростов отдельных агрегатов.

Найдем условия, при которых в данном случае получается минимум затрат. Найдем знак второго дифференциала от S

d²S = d²T +d²W, (1.25)

где

Вторые смешанные частные производные от Т всегда равны нулю, т.к. удельный прирост одного агрегата не зависит от мощности второго агрегата. Поэтому

(1.26)

Очевидно также, что

т.к.

Следовательно, условие d²S  0 имеет место, если

(1.27)

т.е. из неубывающих кривых ₁, ₂, ... _n хотя бы одна является возрастающей. Это означает, что удельные приросты не снижаются при росте активной мощности, а хотя бы у одного из агрегатов возрастают.

2. При учете влияния изменения потерь в сетях, но при неизменности активных нагрузок узловых точек оптимальное распределение активной мощности находится таким образом.

Пусть суммарные потери активной мощности в сетях Р зависят только от величины активных мощностей агрегатов, т.е.

Р = f (Р₁, Р₂, ..., Р_n)

Исходя из уравнений (1.17) – (1.19), получим условия оптимального распределения активной мощности:

(1.28)

откуда

... (1.29)

Уравнения (1.29) совместно с уравнением баланса активных мощностей решают оптимальное распределение активной мощности с учетом изменения потерь в сетях. При этом необходимо знать не только зависимости

_i = f (Р_i),

но и зависимости потерь мощности и частных производных от потерь мощности по активным мощностям агрегатов от Р₁, Р₂, ..., Р_n, т.е.

Р = Ф (Р₁, Р₂, ..., Р_n); = f_i (Р₁, Р₂, ..., Р_n).

Величина  = -  называется удельным приростом энергосистемы при учете потерь в сетях, а выражение - соответственно удельным приростом агрегата i с учетом потерь в сетях.