2.4. Ряд і теорема в.0.Котельникова. Дискретизація неперервних сигналів. Ряд Котельникова.

Як вже відмічалось, при передачі електричних сигналів завади можуть змінювати сигнал. Відновити початковий сигнал значно простіше у тому випадку якщо він дискретний.

Більше того, зовсім немає необхідності відновлювати весь, за виключенням, початковий сигнал, а досить його відновити в дискретні сукупності точок. Але весь сигнал при цьому починає втрачати інформацію. Тому виникає питання, яким чином провести дискретизацію сигналу без втрати його основної інформаційної частини?

Відповідь на питання дає теорема О.В.Котельникова.

Будь - який неперервний сигнал U(t), що не має частот, вищих за , можна точно відновити за його відліками , взятих з кроком дискретизації

однозначне повернення

Доведення теореми.

Отже замість функції U(t) розглядається функція, яка повинна мати подібний спектр як і U(t) в інтервалі частот .

Нехай функція U(t) має обмежений спектр частотою. Тоді:

(1)

Отже наша функція (до речі парна по ) задана на інтервалі Розкладемо її в ряд Фур'є: (2)

це дійсно так. Періодом функції є

Вивід (2)

=

Розрахуємо коефіцієнти розкладу:

(3)

Тепер вернемось до функції U(t).

Здійснимо спектральне представлення

(4)

Розглянемо дискретизовану функцію, задану лише в точках

(5)

Порівняємо вирази (3) та (5).

(6)

Отже

(7)

Відмітимо, що парна функція відносно k. Тоді

;

(8)

Отже спектральна густина може визначатись через відліки сигналу

(9)

Так як спектральна густина однозначно визначає сигнал U(t), а сама може бути однозначно визначена по дискретній функції , то це доводить теорему. Отже для побудови функції U(t), що має обмежені частоти f<F необхідно і достатньо мати сукупність значень дискретизованої функції з кроком дискретизації . Далі здійснюється розрахунок спектральної густини:

та відновлюється вся неперервна функція .

тут вже час не дискретизований!

2.4.1.Ряд Котельникова

Нехай у нас є сигнал у вигляді залежності U(t) з обмеженим спектром частот f<F. Тоді його можна представити виразом: враховуючи (7) і міняючи порядок інтегрування

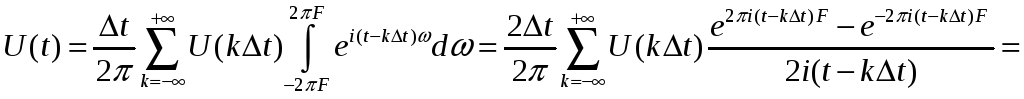з врахуванням

(10)

де

Цей ряд дає можливість однозначно обчислити функцію U(t) з обмеженим зверху спектром через сукупність її дискретизованих значень , де . Цей же ряд можна розглядати як розклад функції U(t) в ортогональний ряд . Ряд (10) називають рядом Котельникова!!!

Функцію - називають функцією відліків. Дослідимо її. Для цього введемо аргумент тоді (11)

Функція має максимум в точці = 0. Графік даної функції має вигляд

При рості функція спадає по модулю, але існує для всіх .

Ширина основної частини спектра рівна . Спектр даної функції дуже цікавий.

Як бачимо, модуль спектру рівномірно постійний на всьому інтервалі зміни кругової частоти .