
- •Г лава I. Линейная алгебра
- •Матрицы и действия над ними
- •Задачи для самостоятельного решения
- •1.2. Определитель матриц
- •Основные свойства определителей
- •Задачи для самостоятельного решения
- •Обратная матрица
- •Задачи для самостоятельного решения
- •1.4. Ранг матрицы
- •Задачи для самостоятельного решения
- •1.5. Системы линейных алгебраических уравнений
- •Задачи для самостоятельного решения
- •Глава II. Векторная алгебра
- •2.1. Векторы на плоскости и в пространстве. Скалярное произведение векторов
Задачи для самостоятельного решения
16. Из Минска в Могилев необходимо перевезти оборудование трех типов: I типа – 95 ед., II типа – 100 ед., III типа –185 ед. Для перевозки оборудования завод может заказать три вида транспорта. Количество оборудования каждого типа, вмещаемого на определенный вид транспорта, приведено в таблице:
|
Тип оборудования |
Вид транспорта |
||
|
Т1 |
Т2 |
Т3 |
|
|
I II III |
3 4 3 |
2 1 5 |
1 2 4 |
Записать в математической форме условия полной перевозки оборудования из Минска в Могилев.
17. Предприятие выпускает продукцию трех видов: А, Б и В. Уровень выпуска лимитируется ограниченностью ресурсов. Все числовые данные приведены в таблице:
|
Ресурсы |
Запас ресурса |
Нормы затрат на единицу продукции |
||
|
А |
Б |
В |
||
|
Сырье, кг Материалы, кг Оборудование, кг |
24 75 10 |
5 7 4 10 5 20 5 2 1 |
||
Записать в математической форме условия, которым должен удовлетворять план выпуска продукции, предполагая полное использование ресурсов.
18. На станции А1 находится 20 т, а на станции А2 – 30 т некоторого однородного груза. Этот груз следует доставить в пункты В1, В2 и В3 в количествах 10 т, 30 т и 10 т соответственно. Стоимость перевозки 1 т груза из пункта А1 в пункты В1, В2 и В3 равна соответственно 4, 9 и 5 ден. ед., а из А2 – 4,8 и 1 ден. ед. Записать в математической форме условия полного удовлетворения потребностей в грузе при транспортных затратах в 300 ден. ед.
19. Методом Гаусса решить систему уравнений:
а)
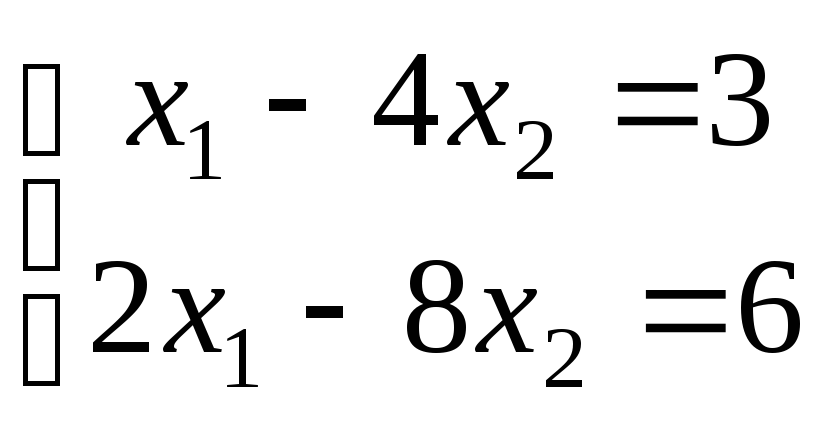 ;
б)
;
б)
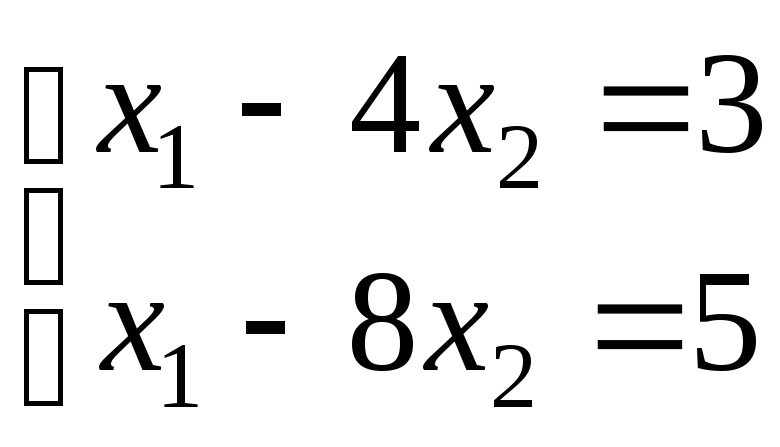 ;
в)
;
в)
 ;
;
г)
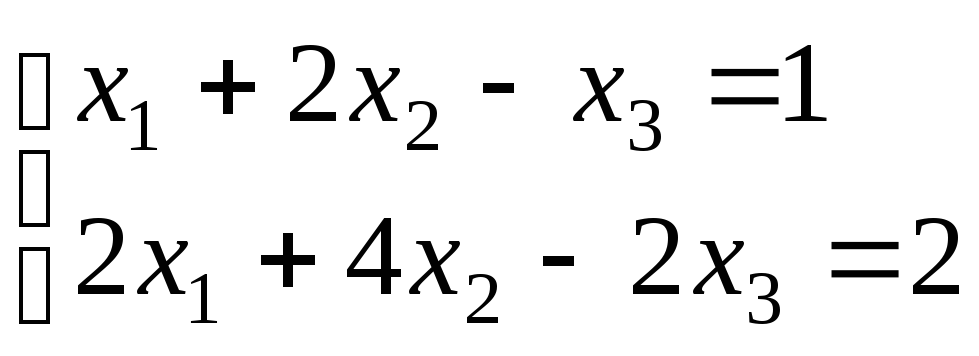 ;
д)
;
д)
 ;
;
е)
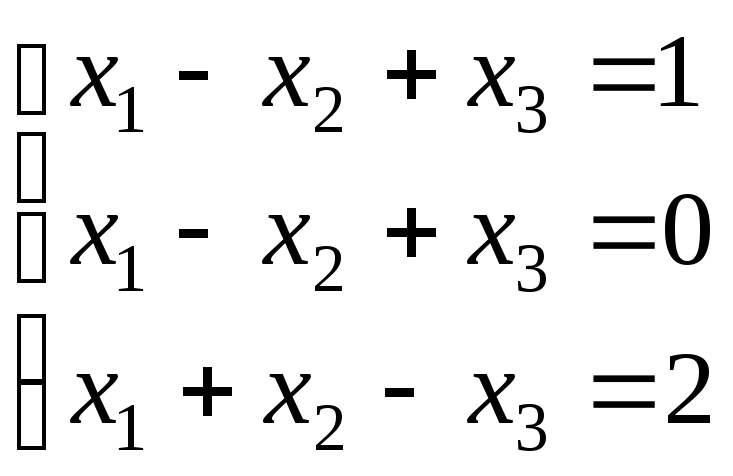 ;
ж)
;
ж)
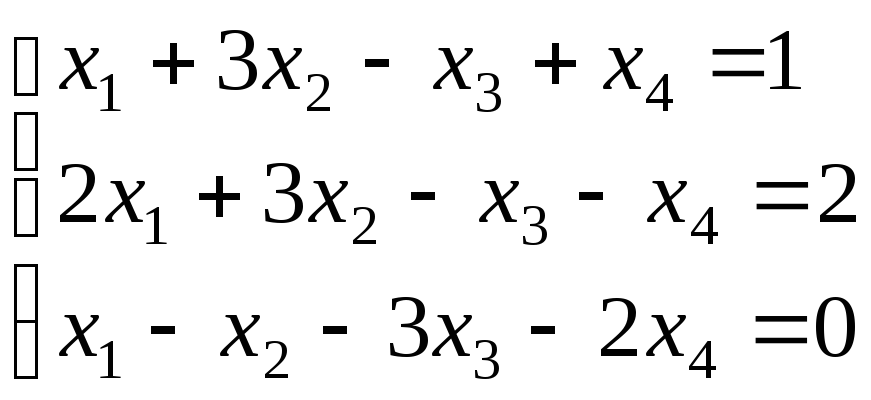 ;
;
з)
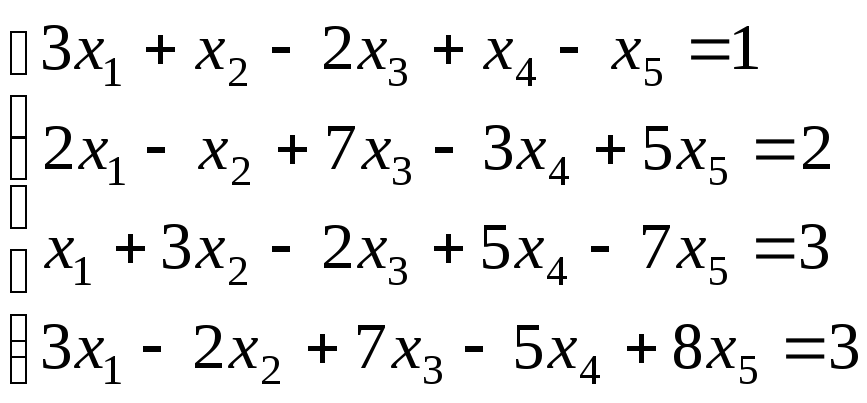 .
.
20. Пользуясь формулами Крамара, решить следующие системы уравнений:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
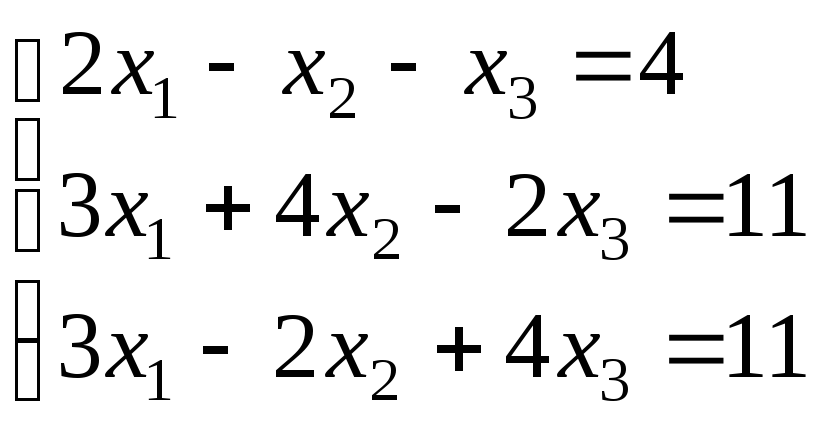 ;
д)
;
д)
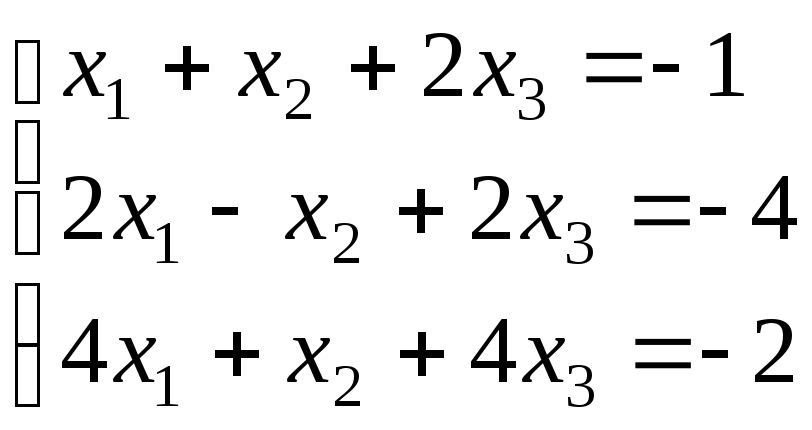 ;
;
е)
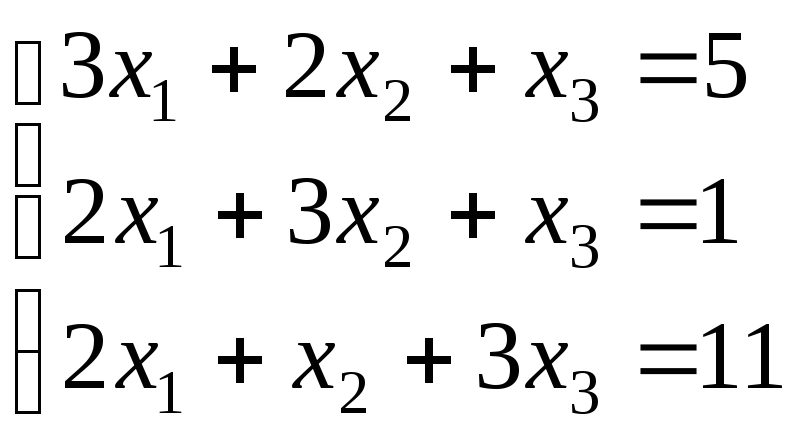 ;
ж)
;
ж)
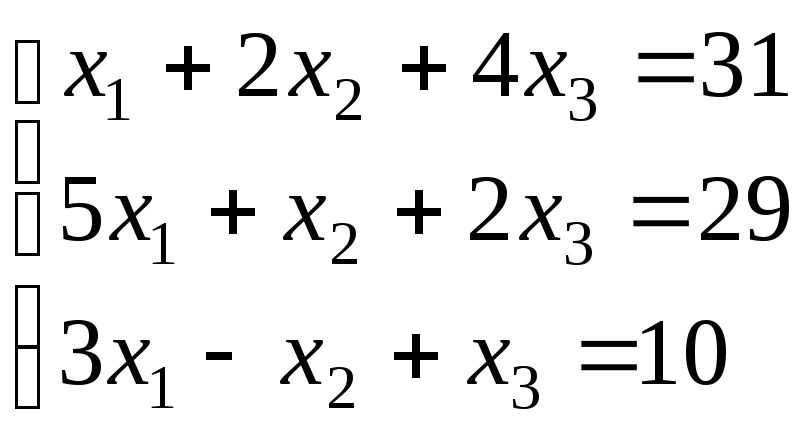 .
.
21. Установить, при
каких значения
![]() данная система уравнений имеет
единственное решение, и найти его:
данная система уравнений имеет
единственное решение, и найти его:
а)
 ;
б)
;
б)
 .
.
Глава II. Векторная алгебра

2.1. Векторы на плоскости и в пространстве. Скалярное произведение векторов
Вектором называется направленный
отрезок
![]() где точка А – начало вектора, точка
В – конец вектора. Если начало и
конец вектора в явном виде не указаны,
то вектор будем обозначать
где точка А – начало вектора, точка
В – конец вектора. Если начало и
конец вектора в явном виде не указаны,
то вектор будем обозначать
![]()
![]() и т. д.
и т. д.
Вектор, у которого начало и конец
совпадают, называется нулевым
вектором и обозначается
![]() .
.
Длиной (модулем) вектора называется
длина его направленного отрезка и
обозначается
![]() ,
,
![]() .
.
Вектор, длина которого равна единице, называется единичным или ортом.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.
Два вектора
![]() и
и
![]() называются равными
называются равными
![]() ,
если они коллинеарны, имеют одинаковую
длину и одинаковое направление.
,
если они коллинеарны, имеют одинаковую
длину и одинаковое направление.
Свободный вектор – это вектор, который можно переносить параллельно самому себе в любую точку пространства (плоскости).
Произведением вектора
![]() на
число
на
число
![]() называется вектор
называется вектор
![]() ,
длина которого
,
длина которого
![]() ;
направление совпадает с направлением
вектора
;
направление совпадает с направлением
вектора
![]() ,
если
,
если
![]() ,
и противоположно ему, если
,
и противоположно ему, если
![]() .
.
Суммой двух векторов
![]() и
и
![]() называется вектор
называется вектор
![]() (рис. 1) и обозначается
(рис. 1) и обозначается
![]() .
.
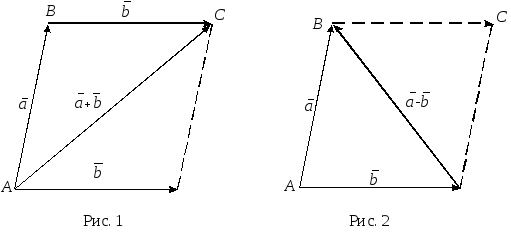
Разностью двух векторов
![]() и
и
![]() называется вектор
называется вектор
![]() и обозначается
и обозначается
![]() (рис. 2).
(рис. 2).
Векторы, лежащие в одной плоскости или на параллельных плоскостях, называются компланарными.
Декартовой прямоугольной системой
координат в пространстве (прямо-угольной)
называется совокупность трех упорядоченных
взаимно перпендикулярных осей координат
ОХ, ОY, OZ с
общим началом в точке О. Орты
координатных осей ОХ, ОY,
ОZ обозначают
![]() соответственно. Векторы
соответственно. Векторы
![]() образуют декартовый прямоугольный
базис в пространстве.
образуют декартовый прямоугольный
базис в пространстве.
Базисом на плоскости
![]() называется упорядоченная пара любых
некомпланарных векторов этой плоскости.
называется упорядоченная пара любых
некомпланарных векторов этой плоскости.
Базисом в пространстве
![]() называется упорядоченная тройка любых
некомпланарных векторов.
называется упорядоченная тройка любых
некомпланарных векторов.
Векторы
![]()
![]() ,
,
![]() в пространстве образуют базис тогда и
только тогда, когда определитель матрицы,
составленной из их координат,
в пространстве образуют базис тогда и
только тогда, когда определитель матрицы,
составленной из их координат,
не равен нулю:
 .
.
Если
![]() – базис на плоскости, то любой вектор
– базис на плоскости, то любой вектор
![]() этой плоскости единственным образом
представляется в виде линейной комбинации
векторов
этой плоскости единственным образом
представляется в виде линейной комбинации
векторов
![]() т. е.
т. е.
![]() .
.
Числа
![]() называют координатами вектора
называют координатами вектора
![]() в базисе
в базисе
![]() и записывают
и записывают
![]() .
.
Если
![]() – базис в пространстве, то любой вектор
– базис в пространстве, то любой вектор
![]() единственным обра-зом представляется
в виде линейной комбинации векторов
единственным обра-зом представляется
в виде линейной комбинации векторов
![]() ,
т. е.
,
т. е.
![]() .
Числа
.
Числа
![]() называют координатами вектора
называют координатами вектора
![]() в базисе
в базисе
![]() и записывают
и записывают
![]() .
.
Координатами точки М в заданной
системе координат называют координаты
ее радиус-вектора
![]() .
В этом случае пишут
.
В этом случае пишут
![]() или
или
![]()
Любой вектор
![]() в пространстве единственным образом
представляется в виде линейной комбинации
векторов
в пространстве единственным образом
представляется в виде линейной комбинации
векторов
![]() т. е.
т. е.
![]() .
Числа
.
Числа
![]() называют декартовыми прямоугольными
координатами вектора
называют декартовыми прямоугольными
координатами вектора
![]() и записывают
и записывают
![]() .
.
Линейные операции над векторами в
координатной форме: пусть
![]() ,
,
![]() ,
тогда
,
тогда
![]() ,
,
![]() .
.
Длина вектора
![]() вычисляется по формуле
вычисляется по формуле
![]() .
(2.1)
.
(2.1)
Если вектор
![]() задан координатами точек
задан координатами точек
![]() и
и
![]() ,
то
,
то
![]() .
(2.2)
.
(2.2)
Скалярным произведением двух
векторов
![]() и
и
![]() называется число, равное произведению
длин этих векторов на косинус угла
называется число, равное произведению
длин этих векторов на косинус угла
![]() между ними:
между ними:
![]() . (2.3)
. (2.3)
Скалярное произведение в координатной форме:
![]() .
(2.4)
.
(2.4)
Из определения скалярного произведения следует, что
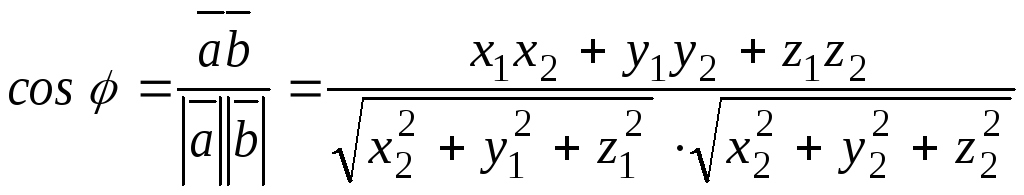 .
(2.5)
.
(2.5)
По значению косинуса находится угол
между ненулевыми векторами
![]() и
и
![]() .
.
Ненулевые векторы
![]() и
и
![]() перпендикулярны (ортогональны)
тогда и только тогда, когда их скалярное
произведение равно нулю:
перпендикулярны (ортогональны)
тогда и только тогда, когда их скалярное
произведение равно нулю:
![]() . (2.6)
. (2.6)
Ненулевые векторы
![]() и
и
![]() коллинеарны тогда и только тогда,
когда их соответствующие координаты
пропорциональны:
коллинеарны тогда и только тогда,
когда их соответствующие координаты
пропорциональны:
![]() .
(2.7)
.
(2.7)
Проекция вектора
![]() на вектор
на вектор
![]() вычисляется по формуле
вычисляется по формуле
![]() .
(2.8)
.
(2.8)
Примеры
-
Даны координаты точек
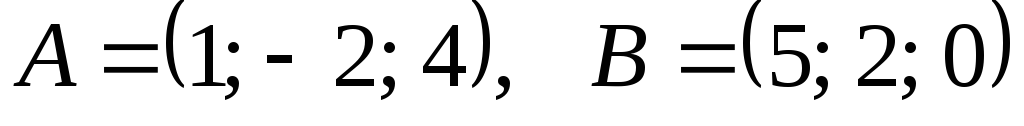 ,
,
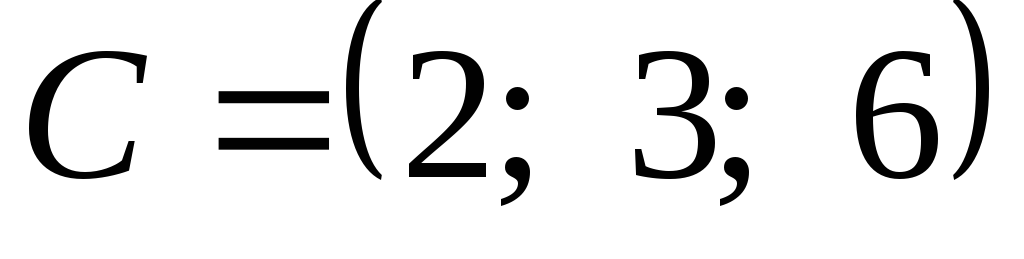 .
.
Вычислить длину вектора
![]() .
.
Р е ш е н и е.
Найдем координаты векторов
![]() по формуле (2.2):
по формуле (2.2):
![]()
![]()
![]() .
.
Найдем координаты
вектора
![]()
![]()
=![]() .
.
Тогда длина вектора
![]() находится по формуле (2.1):
находится по формуле (2.1):
![]() 31,6.
31,6.
-
Упростить выражение
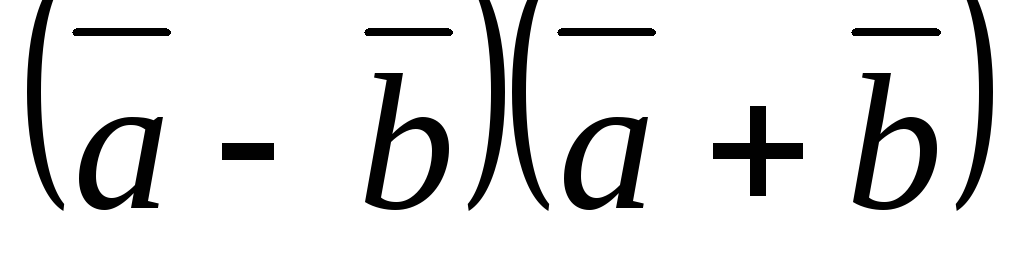 .
.
Р е ш е н и е. Воспользуемся свойствами скалярного произведения:
![]() .
.
-
Определить, перпендикулярны ли векторы
 и
и
 ,
если
,
если
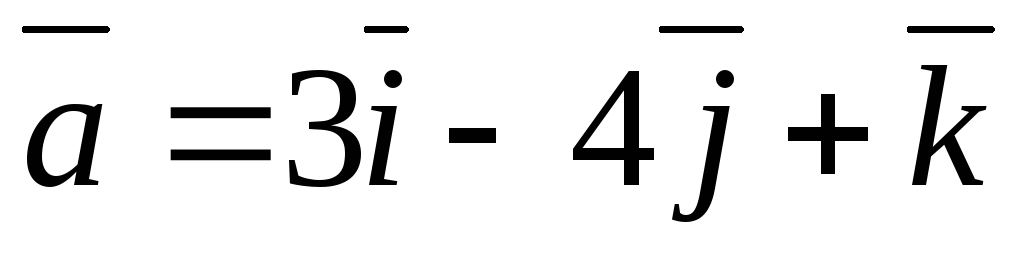 ,
,
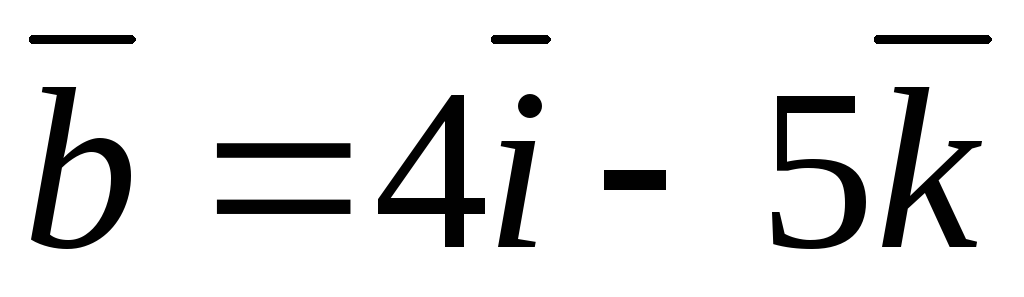 .
.
Р е ш е н и е.
Векторы
![]() и
и
![]() имеют координаты:
имеют координаты:
![]()
Вычислим по формуле (2.4) скалярное произведение
![]() .
.
Следовательно,
векторы
![]() и
и
![]() не перпендикулярны, так как не выполняется
условие перпендикулярности (2.6).
не перпендикулярны, так как не выполняется
условие перпендикулярности (2.6).
-
Найти координаты вектора
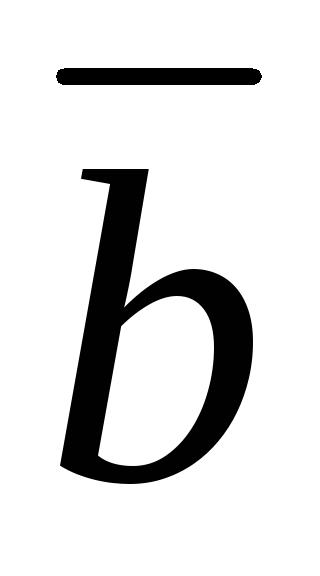 ,
коллинеарного вектору
,
коллинеарного вектору
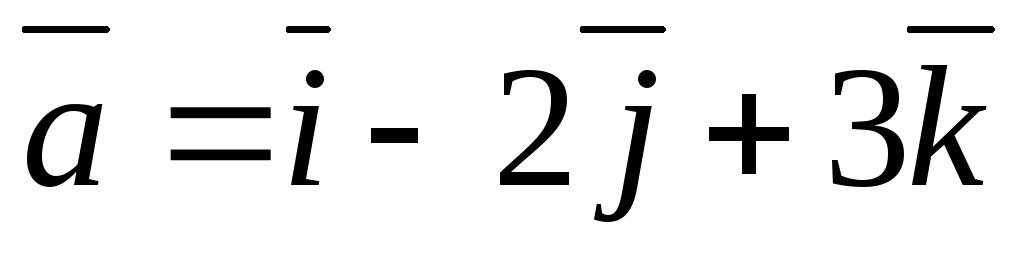 при условии
при условии
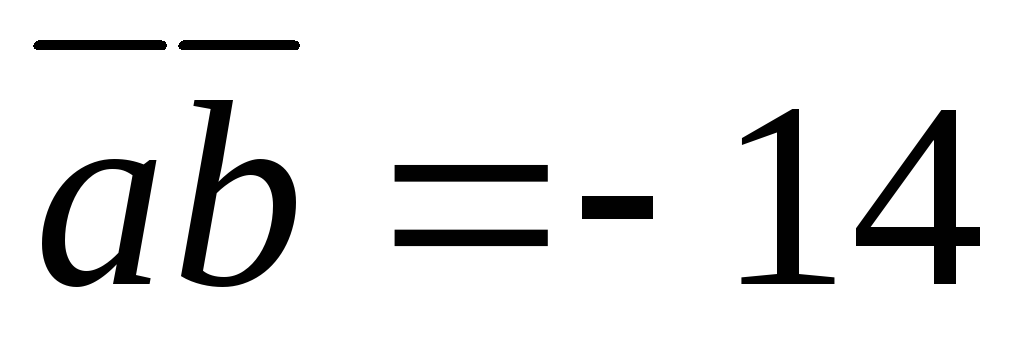 .
.
Р е ш е н и е.
Из условия коллинеарности векторов
(2.7) следует, что существует число
![]() ,
такое что
,
такое что
![]() .
Тогда
.
Тогда
![]() .
.
Из условия задачи
следует
![]() .
.
Тогда
![]() .
.
Следовательно,
![]() или
или
![]() .
.
-
При каком значении параметра
 векторы
векторы
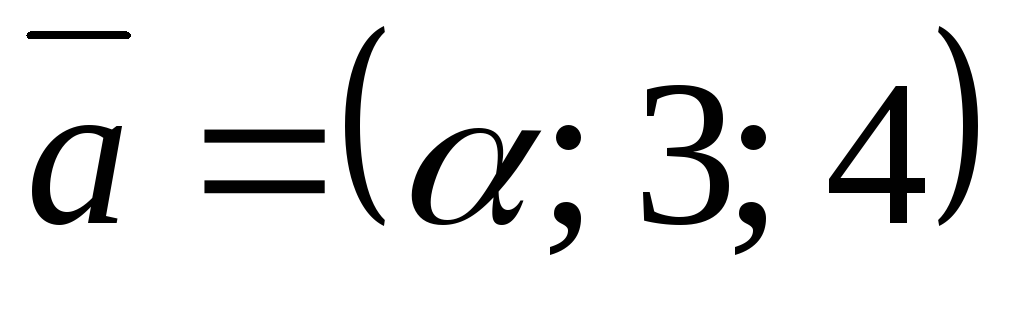 и
и
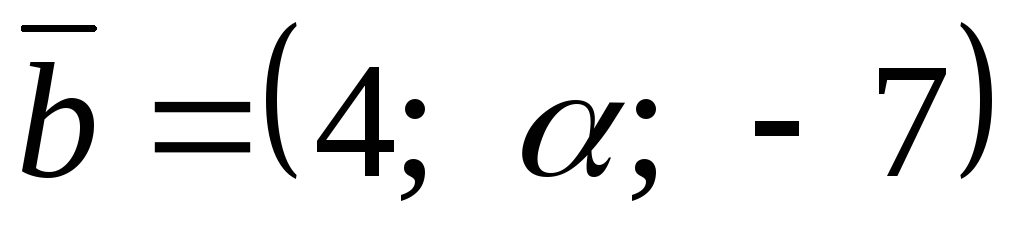 :
:
-
коллинеарны;
-
перпендикулярны?
Р е ш е н и е. 1) Из условия коллинеарности векторов (2.7) следует
![]() .
.
Из пропорции
![]() найдем значение
найдем значение
![]() .
.
