Подсказка

Числа a, b, c - корни некоторого многочлена третьей степени. Чему равны коэффициенты этого многочлена?

Решение

Рассмотрим многочлен P(x)=(x-a)(x-b)(x-c). Числа a, b, c - корни этого многочлена. Раскроем скобки и найдем коэффициенты этого многочлена: P(x)=(x-a)(x-b)(x-c)=x³-(a+b+c)x²+(ab+bc+ca)x-abc. (По существу, эта выкладка есть доказательство теоремы Виета для многочлена третьей степени). Таким образом, из условия следует, что P(x)=x³-px²+qx-r, где p, q, r - положительные числа. Если x - неположительное число, то каждое их слагаемых x³, -px², qx неположительно, следовательно, в этом случае P(x)<0. Итак, многочлен P(x) не имеет неположительных корней, т.е. его корни a, b, c - положительны, что и требовалось доказать.

12. Числа x, y, z удовлетворяют системе

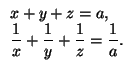
Докажите, что хотя бы одно из этих чисел равно a.

13. Дискриминант кубического уравнения. Пусть уравнение x³ + px + q = 0 имеет корни x₁, x₂ и x₃. Выразите через p и q дискриминант этого уравнения

D = (x₁ - x₂)²(x₂ - x₃)²(x₃ - x₁)².

14. Постройте многочлен, корни которого равны квадратам корней многочлена x³ + x² - 2x - 1 = 0.

15. Известно, что x₁, x₂, x₃ — корни уравнения

x³ - 2x² + x + 1 = 0.

Составьте новое уравнение, корнями которого были бы числа y₁ = x₂x₃, y₂ = x₁x₃, y₃ = x₁x₂.

16. Найдите все корни уравнения (z - 1)ⁿ = (z + 1)ⁿ. Чему равна сумма квадратов корней данного уравнения?

Решение

z_k = itg  - + = ictg      (1 k n - 1). Для нахождения суммы квадратов корней раскроем в уравнении скобки по формуле бинома Ньютона и сделаем сокращения:

C_n^{n - 1}z^{n - 1} + C_n^{n - 3}z^{n - 3} +...= 0.

По теореме Виета

(z₁,..., z_{n - 1}) = 0,

(z₁,..., z_{n - 1}) = = .

Далее, применяя результат задачи 6.107 , д), находим

z₁² + z₂² +...+ z_{n - 1}² = - .

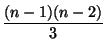17. Докажите, что равенство

4p³ + 27q² = 0

является необходимым и достаточным условием для совпадения по крайней мере двух корней уравнения x³ + px + q = 0.

18. Целые числа a, b и c таковы, что числа ++ и + + тоже целые. Докажите, что | a| = | b| = | c|.

Решение

  Первый способ. Пусть утверждение задачи не верно. Числа a, b и c можно сократить на их общий множитель, поэтому будем считать, что НОД(a, b, c) = 1. Пусть одно из чисел не равно ±1, можно считать, что это число a. Пусть p — любой простой делитель числа a. Так как числа взаимно просты в совокупности, p не делит число b или p не делит число c. Рассмотрим второй случай (первый случай аналогичен).

Введем обозначение: k(x) — максимальная степень p в разложении x на простые множители. Можно считать, что k(a)k(b) (мы знаем, что k(c) = 0).

Имеем

+ + = .

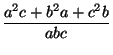Число p входит в знаменатель в степени k(a) + k(b). Значит, числитель делится на p^{k(a) + k(b)}. Покажем, что это не так. Число p входит в a²c в степени 2k(a)k(a) + k(b), в b²a -- в степени k(a) + 2k(b)k(a) + k(b), а в c²b — в степени k(b) < k(a) + k(b). Значит, a²c + b²a делится на p^{k(a) + k(b)}, а c²b -- не делится на p^{k(a) + k(b)}. Поэтому сумма этих чисел не делится на p^{k(a) + k(b)} — противоречие.

Второй способ. Введем обозначения: x = , y = , z = . Тогда xyz = 1 и

xy + yz + zx = = + + = + +

-- целое число. Рассмотрим многочлен

P(t) = t³ - (x + y + z)t² + (xy + yz + zx)t - xyz.

По доказанному, все коэффициенты этого многочлена целые. Кроме того, коэффициент при старшем члене t³ равен единице. Значит, все рациональные корни этого многочлена — целые (см. комментарий). Согласно обратной теореме Виета, x, y и z — корни этого многочлена. Значит, x, y и z -- целые числа, но xyz = 1, так что x = ±1, y = ±1, z = ±1. Это равносильно тому, что | a| = | b| = | c|.

Комментарий. Докажем использованное утверждение.

Пусть f (x) = a₀ + a₁x + ... + a_nxⁿ — многочлен с целыми коэффициентами.

Теорема. Пусть — несократимая дробь, которая является корнем многочлена f (x). Тогда p| a₀, q| a_n.

Набросок доказательства. Докажем первое утверждение. Условие f[b] = 0 можно переписать так:

a0q^n + a1pq^n - 1 + ... + anp^n = 0.

(2)

Пусть l — простое число. Достаточно доказать, что максимальная степень l, входящая в разложение p на простые множители, не превосходит максимальной степени l, входящей в разложение числа a₀ на простые множители. Пусть это не так, т. е. найдется такое x, что p делится на l^x, а a₀ не делится на l^x. Так как дробь несократима, q не делится на l, поэтому в левой части равенства (*) первый член не делится на l^x, а остальные делятся, но это невозможно.

Следствие. Если a_n = 1, то любой рациональный корень многочлена f (x) является целым.

19. Числа x, y, z удовлетворяют равенству

x + y + z - 2(xy + yz + xz) + 4xyz = .

Докажите, что хотя бы одно из них равно 1/2.
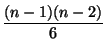