
Решение
Заметим, что
x + y
+ z
- 2(xy
+ yz
+ xz)
+ 4xyz
-
![]() =
=
![]() (2x
- 1)(2y
- 1)(2z
- 1).
(2x
- 1)(2y
- 1)(2z
- 1).
Если левая часть равенства равна нулю, то хотя бы один множитель справа равен нулю. Значит, одно из чисел x, y, z равно 1/2.
Комментарии. 1o. Как догадаться до разложения на множители? Обозначим этот многочлен через P(x, y, z). Воспользуемся общим утверждением: если многочлен от нескольких переменных тождественно обращается в нуль при x = a, то многочлен делится на x - a. Если x = 1/2, то P(x, y, z) = 0. Значит, P(x, y, z) делится на x - 1/2. Аналогично, P(x, y, z) делится на y - 1/2 и z - 1/2. Поэтому P(x, y, z) равен (x - 1/2)(y - 1/2)(z - 1/2) с точностью до умножения на константу.
2o. Другой способ: согласно обратной теореме Виета P(x, y, z) = - 4f (1/2), где
f (t) = (t - x)(t - y)(t - z).
20. Целые числа a, b и c таковы, что числа a/b+b/c+c/a и a/c+c/b+b/a тоже целые. Докажите, что |a|=|b|=|c|.
Подсказка
Можно использовать соображения делимости или рассмотреть многочлен третьей степени, корнями которого являются числа a/c, c/b, b/a.
Решение
Пусть a/b=x, b/c=y, c/a=z. Очевидно, xyz=1. Обозначим x+y+z через k, а xy+yz+zx через m. Тогда, k=x+y+z=a/b+b/c+c/a - целое. Также m=xy+yz+zx=(a/b)*(b/c)+(b/c)*(c/a)+(c/a)*(a/b)=a/c+c/b+b/a - целое. По обратной теореме Виета числа x,y,z являются корнями уравнения x3-kx2+mx-1=0. Нетрудно показать, что если рациональные числа являются корнями многочлена с целыми коэффициентами и старшим коэффициентом, равным 1, то они целые. Значит, x,y,z - целые, но xyz=1. Поэтому |x|=|y|=|z|=1, откуда |a|=|b|=|c|, что и требовалось доказать.
21. Решите системы: а)
![]()
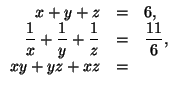
б)
![]()
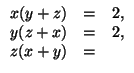
в)
![]()
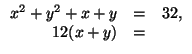
г)
![]()

д)
![]()
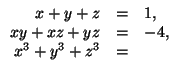
е)
![]()
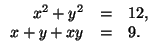
22. Метод Лобачевского. Пусть многочлен
P(x) = xn + an - 1xn - 1 +...+ a1x + a0
имеет корни x1, x2, ..., xn, причем | x1| > | x2| >...> | xn|. В задаче 6.42 был предъявлен способ построения многочлена Q(x) степени n, корнями которого являются числа x12, x22, ..., xn2. На основе этого рассуждения Лобачевский придумал метод для приближенного поиска корней многочлена P(x). Он заключается в следующем. Строится последовательность многочленов P0(x), P1(x), P2(x),...такая, что P0(x) = P(x) и многочлен Pk(x) имеет корни x12k,..., xn2k. Пусть
Pk(x) = xn + an - 1(k)xn - 1 +...+ a1(k)x + a0(k).
Докажите, что
а)
![]()
![]() -
an
- 1(k)
-
an
- 1(k)![]() = x1;
б)
= x1;
б)
![]()
![]() -
-
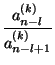
![]() =
xl
(1
=
xl
(1
![]() l
l
![]() n).
n).
23. Докажите, что ни при каком целом A многочлен 3x2n + Axn + 2 не делится на многочлен 2x2m + Axm + 3.
Решение
Предположим, что многочлен
3x2n + Axn + 2
делится на многочлен 2x2m + Axm + 3.
Тогда любой корень многочлена
2x2m + Axm + 3
является также корнем многочлена
3x2n + Axn + 2.
Если xi
— корень многочлена 2x2m + Axm + 3,
то xim = ![]() = α1,2.
Можно считать, что x1m = α1
и x2m = α2.
Пусть β1,2 =
= α1,2.
Можно считать, что x1m = α1
и x2m = α2.
Пусть β1,2 = ![]() — корни квадратного трёхчлена
3x2 + Ax + 2.
Первый случай.
A2 - 24 > 0.
В этом случае |α1| ≠ |α2|,
поэтому x1n = β1
и x2n = β2.
С одной стороны, |x1x2| =
— корни квадратного трёхчлена
3x2 + Ax + 2.
Первый случай.
A2 - 24 > 0.
В этом случае |α1| ≠ |α2|,
поэтому x1n = β1
и x2n = β2.
С одной стороны, |x1x2| = ![]() =
= ![]() < 1,
а с другой стороны |x1x2| =
< 1,
а с другой стороны |x1x2| = ![]() =
= ![]() > 1.
Приходим к противоречию.
Второй
случай. A2 - 24 ≤ 0.
В этом случае |α1| = |α2| =
> 1.
Приходим к противоречию.
Второй
случай. A2 - 24 ≤ 0.
В этом случае |α1| = |α2| = ![]() и |β1| = |β2| =
и |β1| = |β2| = ![]() .
Поэтому, с одной стороны, |x1| =
.
Поэтому, с одной стороны, |x1| = ![]() =
= ![]() > 1,
а с другой стороны, |x1| =
> 1,
а с другой стороны, |x1| = ![]() =
= ![]() < 1.
Снова приходим к противоречию
< 1.
Снова приходим к противоречию
24. Докажите, что при нечетном n > 1 справедливо равенство
![]()
![]() =
=
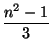 .
.
