
- •7. Повторення досліджень. Теорема Бернуллі
- •Лекція №5 Тема: Випадкові величини
- •3. Означення функції розподілу та її властивості
- •Лекція №6 Тема: Основи математичної статистики. Вибірковий метод та способи відбору.
- •4. Варіаційний ряд. Полігон і гістограма.
- •I. Законспектувати в зошит з практичних робіт:
- •1). Методологія теорії ймовірностей
- •III. Ознайомитись з типовими задачами, які розглядатимуться на занятті
- •Практичне заняття №2
- •Практичне заняття №3
- •I. Законспектувати в зошит для практичних робіт:
- •Практичне заняття №4
- •IV. Ознайомитись з типовими задачами, які розглядатимуться на занятті
- •Практичне заняття №5
- •IV. Ознайомитись з типовими задачами, які розглядатимуться на занятті
- •Практичне заняття №6
- •III. Ознайомитись з типовими задачами, які розглядатимуться на занятті
- •Практичне заняття №7
- •I. Законспектувати в зошит для практичних робіт:
- •Практичне заняття №8
- •Практичні заняття №9
- •Практичне заняття №10
- •Практичне заняття №11
- •Практичне заняття №12
- •I. Повторити:
- •Практичне заняття №13
- •I. Законспектувати в зошит для практичних робіт:
- •Практичне заняття №14
- •I. Законспектувати в зошит для практичних робіт:
- •Практичне заняття №15
- •Практичне заняття №16
- •I. Законспектувати в зошит для практичних робіт:
- •IV. Ознайомитись з типовими задачами, які розглядатимуться на занятті
- •Практичне заняття №17
- •I. Законспектувати в зошит для практичних робіт:
- •IV. Ознайомитись з типовими задачами, які розглядатимуться на занятті
- •Практичні заняття №18
- •I. Законспектувати в зошит для практичних робіт:
- •IV. Ознайомитись з типовими задачами, які розглядатимуться на занятті
- •Перелік питань до іспиту з теорії ймовірностей і математичної статистики
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
КИЇВСЬКИЙ ІНСТИТУТ БІЗНЕСУ ТА ТЕХНОЛОГІЙ
ЖИТОМИРСЬКА ФІЛІЯ
«Математика для економістів: теорія ймовірностей,
математична статистика»
Укладач:
Шевчук В.А
Житомир 2010
ЛЕКЦІЙНИЙ КУРС
МОДУЛЬ 1. ОСНОВНІ ПОЛОЖЕННЯ ТЕОРІЇ ЙМОВІРНОСТЕЙ
Лекція №1
Тема: Теорія ймовірностей як наука, її предмет та завдання
-
Вступ. Загальні відомості про теорію ймовірностей
-
Основні поняття теорії ймовірностей
-
Методологія теорії ймовірностей
3. Методологія теорії ймовірностей
Під терміном «метод» (шлях дослідження або пізнання, теорія, наука) розуміють сукупність прийомів або теоретичного опанування дійсності, підпорядкованих вирішенню конкретного завдання.
Загальним методом пізнання для всіх наук, у тому числі для теорії ймовірностей, є діалектичний метод. Відповідно до основоположних принципів і законів діалектики всі суспільні явища і процеси, які вивчаються теорією ймовірностей, знаходяться в постійному русі і розвитку, не ізольовано одне від одного, а у взаємозв'язку і взаємозалежності.
Методи теорії ймовірностей широко застосовуються в різних галузях природознавства й техніки. Автоматичне управління виробничими процесами, створення автоматичних радіолокаційних станцій і автоматичних математичних машин, проблема автоматичного управління польотами літаків і інші технічні проблеми автоматики й телемеханіки викликали бурхливий розвиток теорії автоматичного регулювання як теоретичної основи автоматики й телемеханіки. Але теорія автоматичного регулювання не могла досить повно охопити процес роботи автоматичних систем без використання імовірнісних методів (особливо теорії випадкових функцій), тому що в будь-якій автоматичній системі є джерела постійно діючих випадкових явищ, які впливають на весь процес роботи системи.
В економічному просторі теорія ймовірностей стала основою для математичної, соціально-економічної та галузевих статистик для планування та організації суспільного виробництва.
Методологічною основою для вивчення ймовірних процесів стали методи матричної алгебри, розрахунково-конструктивний метод, методи розв’язання систем алгебраїчних рівнянь, методологія диференціального числення.
Лекція №2
Тема: Визначення ймовірності події
-
Поняття про ймовірність події. Статистичне визначення ймовірності події
-
Класичне визначення ймовірності події
-
Геометричне визначення ймовірності події
Лекція №3-4
Тема: Основні положення теорії ймовірностей
-
Аксіоми теорії ймовірностей
-
Теорема додавання ймовірностей для несумісних подій
-
Теорема множення ймовірностей
-
Теорема додавання для сумісних подій
-
Формула повної ймовірності
-
Теорема гіпотез (формула Бейєса)
-
Повторення досліджень. Теорема Бернуллі
6. Теорема гіпотез (формула Бейєса)
Поставимо наступне завдання. Є повна група несумісних гіпотез Н1,Н2,..., Нп. Відомі ймовірності кожної з гіпотез Р(Н1), Р (Н2),..., Р(Нп). Припустимо, що відбувається дослід і в результаті здійснюється деяка подія А, ймовірності якої по кожній з гіпотез відомі, тобто відомі Р(А/Н1), Р(А/Н2),..., Р(А/Нп). Запитується, які ймовірності мають гіпотези Н1,Н2,..., Нп у зв'язку з появою події А? Інакше кажучи, нас цікавлять умовні ймовірності Р (Ні\А) для кожної гіпотези.
Відповідь на поставлене завдання дає наступна теорема гіпотез.
Теорема гіпотез. Ймовірність гіпотези після випробування дорівнює добутку ймовірності гіпотези до випробування на відповідну їй умовну ймовірність події, що відбулося при випробуванні, діленому на повну ймовірність цієї події:
 .
.
Ця формула називається формулою Байєса.
7. Повторення досліджень. Теорема Бернуллі
Нехай проводиться кілька випробувань, у результаті яких може з'явитися подія А з певною ймовірністю. Якщо ймовірність події А в кожному випробуванні не залежить від інших випробувань, то такі випробування ми раніше визначили як незалежними щодо події А.
Поставимо наступну задачу – визначити ймовірність того, що в результаті проведення n незалежних випробувань деяка подія А наступить рівно k разів, якщо в кожному із цих випробувань дана подія наступає з постійною ймовірністю Р(А)=р.
Шукану ймовірність будемо позначати Рk;n „. Наприклад, символ Р4,10 означає, що в десяти випробуваннях подія А з'явиться рівно 4 рази.
Безпосереднє застосування теорем додавання й множення ймовірностей для рішення поставленої задачі зі збільшенням числа випробувань приводить до дуже громіздких обчислень. Тому виникає необхідність застосування менш трудомістких способів розрахунку.
Один
з таких способів заснований на застосуванні
формули Бернуллі.
Припустимо,
що в однакових умовах проводиться п
незалежних
випробувань, після кожного з яких може
бути
настання
або
події А
з
імовірністю
Р(А)
= р, або
йому протилежна
подія 
 з імовірністю
з імовірністю
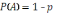
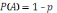 .
.
Позначимо через Аi (i=1, 2, .... n) настання події А в i-му випробуванні.
Нас
цікавить імовірність того, що подія А
при
n
випробуваннях
наступає рівно k
разів,
а в інших, що залишилися n–k
випробуваннях
наступить їй протилежна подія
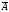 .
При
цьому подія А
в
п
випробуваннях
може з'явитися рівно k
раз
у різних послідовностях або комбінаціях,
число яких дорівнює числу комбінацій
з n
елементів
по k,
тобто
Сn(k).
.
При
цьому подія А
в
п
випробуваннях
може з'явитися рівно k
раз
у різних послідовностях або комбінаціях,
число яких дорівнює числу комбінацій
з n
елементів
по k,
тобто
Сn(k).
Оскільки всі комбінації подій у даній задачі, є несумісними подіями і нам байдуже, у якій саме послідовності з'явиться подія А та в якій послідовності з'явиться протилежна їй подія, то, застосовуючи теорему додавання ймовірностей для несумісних подій, одержимо формулу для визначення ймовірності події, що повторюється n раз і в k випадках має місце дана подія А.
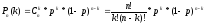
Дана формула називається формулою Бернуллі.
Якщо кількість випробувань дуже велика (n>10), то застосування такої формули приводить до дуже громіздких розрахунків. В таких випадках використовують теореми Муавра – Лапласа та формулу Пуассона.
Локальна теорема Муавра-Лапласа використовується при наближеному обчисленні ймовірності Рп (k) (тим точніше, чим більше п) в схемі Бернуллі:
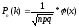 ,
,
де
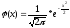 – функція нормального розподілу
Пуассона, значення якої можна знайти
за допомогою таблиці. Змінну х
шукають за такою формулою:
– функція нормального розподілу
Пуассона, значення якої можна знайти
за допомогою таблиці. Змінну х
шукають за такою формулою:
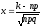
Дана функція (х) має такі властивості:
1)
функція
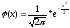 парна,
тобто (-
х) =
(х),
парна,
тобто (-
х) =
(х),
2)
функція
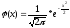 спадна і при х
>
3,99
(х)
=
0.
спадна і при х
>
3,99
(х)
=
0.
Таким чином, на практиці локальна теорема Муавра-Лапласа використовується таким чином: спочатку шукають х, потім за допомогою таблиці розподілу Пуассона шукають (х), а далі за формулою визначають Рп (k)
При досить великому п і малому р {р < 0,01) застосовується формула Пуассона:
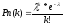 ,
де
,
де
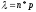
Інтегральна
теорема Лапласа
використовується
при наближеному обчисленні ймовірності
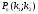 того,
що в n
випробуваннях подія А
відбудеться
не менше k1,
і не більше k2
разів. Формула визначення такої
ймовірності:
того,
що в n
випробуваннях подія А
відбудеться
не менше k1,
і не більше k2
разів. Формула визначення такої
ймовірності:
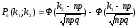
де
Ф(х)=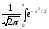 –
функція
Лапласа, значення якої задано таблицею.
–
функція
Лапласа, значення якої задано таблицею.
Функція Ф(х) має такі властивості:
1) Ф(х) визначена для всіх х на множині дійсних чисел,
2) Ф(х) є зростаючою функцією,
3) Ф(х) є непарною, тобто Ф(–х)=–Ф(х),
4) для всіх х> 5 маємо Ф(х)=0,5.
МОДУЛЬ 2. ТЕОРІЯ ВИПАДКОВИХ ПРОЦЕСІВ
