
- •3. Аналитическая геометрия в пространстве
- •3.1. Плоскость в пространстве
- •3.2. Уравнение прямой в пространстве
- •2.3. Проекция вектора на заданную ось. Координаты вектора в декартовой системе координат
- •2.4. Скалярное произведение двух векторов
- •2.5. Векторное и смешанное произведения векторов
- •2.2. Векторы. Линейные операции над векторами
- •1.3. Умножение матриц
- •1.4. Обратная матрица
- •1.5. Ранг матрицы. Элементарные преобразования матриц
- •1.7. Системы линейных алгебраических уравнений
- •1.8. Метод Гаусса решения систем линейных уравнений (метод последовательного исключения неизвестных)
- •1.9. Метод Крамера решения системы n линейных уравнений с n неизвестными
Свойства
определителя.
Минором
элемента aij
определителя порядка n
называется определитель порядка
Алгебраическим
дополнением
элемента aij
называется
величина Aij = (–1)i+jMij.
Свойства
определителей:
Значение
определителя не изменится, если заменить
все его строки соответствующими по
номеру столбцами (транспонировать).
Если
поменять местами две строки, определитель
изменит знак.
Если
в двух строках элементы с одинаковыми
номерами пропорциональны, то определитель
равен нулю.
Если
каждый элемент строки определителя
умножить на число k,
то определитель увеличится в k
раз.
Следствие:
общий множитель всех элементов строки
можно выносить за знак определителя.
Сумма
попарных произведений элементов одной
строки на алгебраические дополнения
элементов с теми же номерами другой
строки равна нулю.
Определитель
не изменит своего значения, если к
элементам одной строки прибавить
элементы с теми же номерами столбцов
другой строки, умноженные на одно и то
же число.
Все
свойства определителя, сформулированные
для строк, справедливы и для столбцов.
Определитель
равен сумме попарных произведений
элементов какой-либо строки (столбца)
на их алгебраические дополнения, т.е.
разложение определителя по элементам
i-й
строки
Введем
обозначения: Si
– i-я
строка; Rj
– j-й
столбец,
Пусть
Если
число строк матрицы В
равно числу столбцов матрицы А,
то матрица В
согласована с матрицей А.
Произведением
матрицы А
на согласованную матрицу В
называется матрица
Квадратная
матрица А
называется невырожденной
или неособенной,
если
Матрица
Невырожденная
матрица А
имеет обратную, причем единственную,
матрицу.
Покажем,
как вычисляется обратная матрица. Пусть
задана
Если
в заданной прямоугольной матрице А
размерности
Рангом
матрицы А
называется наивысший порядок минора,
отличного от нуля. Элементарными
преобразованиями матриц называются
такие преобразования, при которых не
изменяется ранг матрицы. Например,
элементарными являются следующие
преобразования:
перемена
местами строк;
транспонирование;
умножение
строки на число;
замена
строки матрицы на строку,
полученную
сложением этой строки с другой, умноженной
на число.
При
элементарных преобразованиях ранг
матрицы не изменяется, поэтому, чтобы
найти ранг произвольной матрицы, можно
элементарными
преобразованиями привести ее к
трапецеидальной матрице.
Система
m
алгебраических
уравнений с n
неизвестными вида
называется
системой
линейных уравнений.
Матрица
коэффициентов при неизвестных
называется
матрицей
системы
уравнений.
Числа
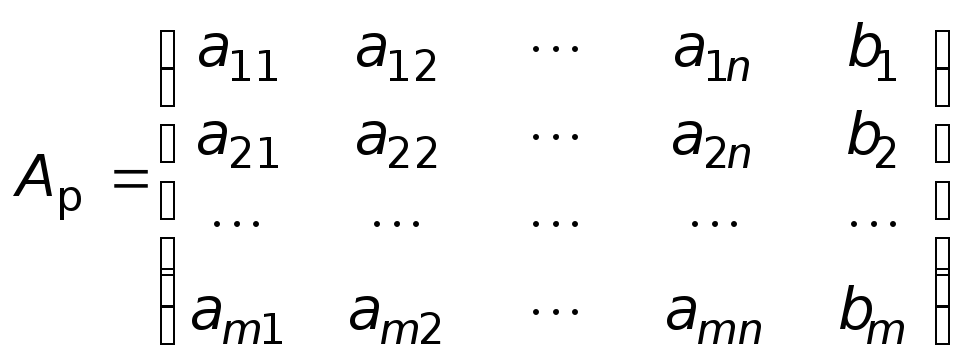
Расширенной
матрицей
системы называется матрица размерности
Если
Решить
систему уравнений (1) означает найти
все наборы чисел
Система
уравнений называется совместной,
если имеет хотя бы одно решение.
Система
m
линейных уравнений с n
неизвестными совместна
тогда и только тогда, когда
Если
система имеет бесконечное множество
решений, то
Метод
позволяет получить решение совместной
системы любой размерности или определить,
что система уравнений несовместна.
Приводя
матрицу системы и расширенную матрицу
к трапецеидальной, определяют ранг
матриц, а следовательно, и структуру
решения исходной системы. Выполняя
элементарные преобразования только
над строками матриц, на каждом шаге
получают матрицу системы уравнений,
имеющую те же решения, что исходная
система линейных уравнений. Выписав
систему уравнений, соответствующую
последней матрице, «обратным ходом»
вычисляют неизвестные.
Рассмотрим
систему n
алгебраических линейных уравнений с
n
неизвестными:
Определителем
системы
называется определитель матрицы системы
Обозначим
Теорема
Крамера.
Если определитель системы уравнений (2)
![]() ,
который получится, если из исходного
определителя вычеркнуть i-ю
строку и
j-й
столбец, обозначаемый Mij.
,
который получится, если из исходного
определителя вычеркнуть i-ю
строку и
j-й
столбец, обозначаемый Mij.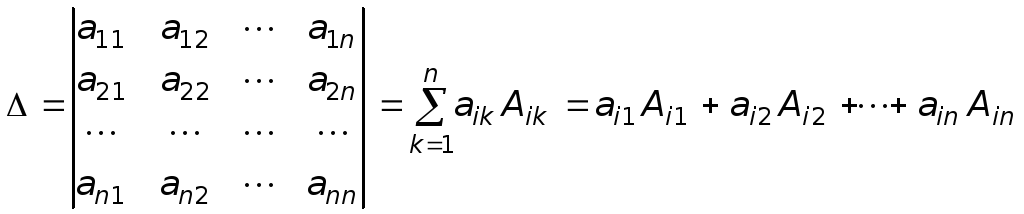 ,
а разложение по элементам j-го
столбца
,
а разложение по элементам j-го
столбца
![]() .
.![]() – сложить поэлементно (т.е. попарно
элементы i-й
и e-й
строк с одинаковыми номерами столбцов)
строки
– сложить поэлементно (т.е. попарно
элементы i-й
и e-й
строк с одинаковыми номерами столбцов)
строки
![]() и Se.
и Se.1.3. Умножение матриц
![]() ,
,
![]() .
.![]() ,
элемент
,
элемент
![]() которой равен сумме попарных произведений
элементов i-й
строки матрицы А
на соответствующий элемент j-го
столбца матрицы В,
т.е.
которой равен сумме попарных произведений
элементов i-й
строки матрицы А
на соответствующий элемент j-го
столбца матрицы В,
т.е.![]()
1.4. Обратная матрица
![]() .
.![]() называется обратной
матрицей
для квадратной матрицы А,
если
называется обратной
матрицей
для квадратной матрицы А,
если
![]() .
.![]() ,
причем
,
причем
![]() .
Тогда
.
Тогда
![]() ,
где
,
где
![]() – союзная матрица матрицы А,
где
– союзная матрица матрицы А,
где
![]() – алгебраическое дополнение элемента
– алгебраическое дополнение элемента
![]() матрицы А.
Обратную матрицу
матрицы А.
Обратную матрицу
![]() для данной матрицы
для данной матрицы
![]() можно получить, приведя элементарными
преобразованиями матрицу А
к единичной и выполнив над
можно получить, приведя элементарными
преобразованиями матрицу А
к единичной и выполнив над
![]() те же преобразования, что и над матрицей
А.
Тогда единичная матрица преобразуется
к матрице
те же преобразования, что и над матрицей
А.
Тогда единичная матрица преобразуется
к матрице
![]() .
.1.5. Ранг матрицы. Элементарные преобразования матриц
![]() выделить k столбцов
и k
строк
выделить k столбцов
и k
строк
![]() то определитель, составленный из
элементов, стоящих на пересечении
выделенных k столбцов
и k
строк, называется минором
k-го порядка
матрицы А.
Число различных миноров
k-го
порядка матрицы размерности
то определитель, составленный из
элементов, стоящих на пересечении
выделенных k столбцов
и k
строк, называется минором
k-го порядка
матрицы А.
Число различных миноров
k-го
порядка матрицы размерности
![]() равно
равно
![]()
1.7. Системы линейных алгебраических уравнений
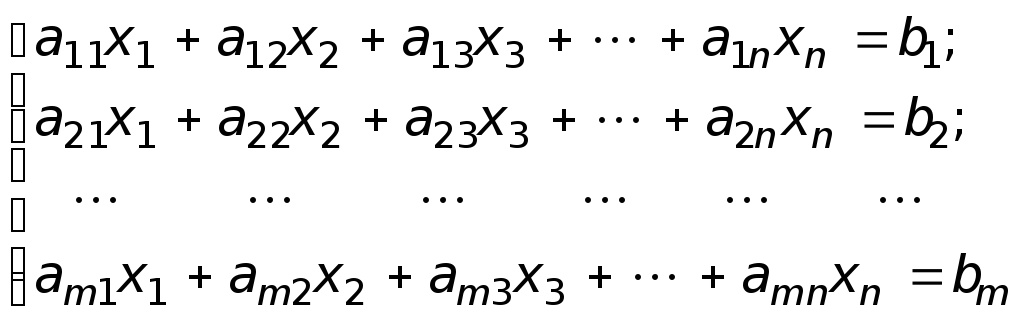 (1)
(1)
![]() называются свободными
членами
уравнений системы.
называются свободными
членами
уравнений системы.![]() :
: .
.![]() = 0
при всех i = 1, 2, ..., m,
то система уравнений называется
однородной.
= 0
при всех i = 1, 2, ..., m,
то система уравнений называется
однородной.![]() ,
при которых каждое из уравнений системы
обращается в тождество.
,
при которых каждое из уравнений системы
обращается в тождество.![]() причем,
если
причем,
если
![]() система имеет единственное решение, а
если
система имеет единственное решение, а
если
![]() ,
то бесконечное множество решений
(теорема Кронекера – Капелли).
,
то бесконечное множество решений
(теорема Кронекера – Капелли).![]() неизвестных принимают произвольные
значения (свободные неизвестные), а
остальные r(A)
неизвестные называются базисными и
вычисляются через свободные неизвестные.
Зависимости, связывающие свободные и
базисные неизвестные, называются общим
решением
системы.
неизвестных принимают произвольные
значения (свободные неизвестные), а
остальные r(A)
неизвестные называются базисными и
вычисляются через свободные неизвестные.
Зависимости, связывающие свободные и
базисные неизвестные, называются общим
решением
системы.1.8. Метод Гаусса решения систем линейных уравнений (метод последовательного исключения неизвестных)
1.9. Метод Крамера решения системы n линейных уравнений с n неизвестными
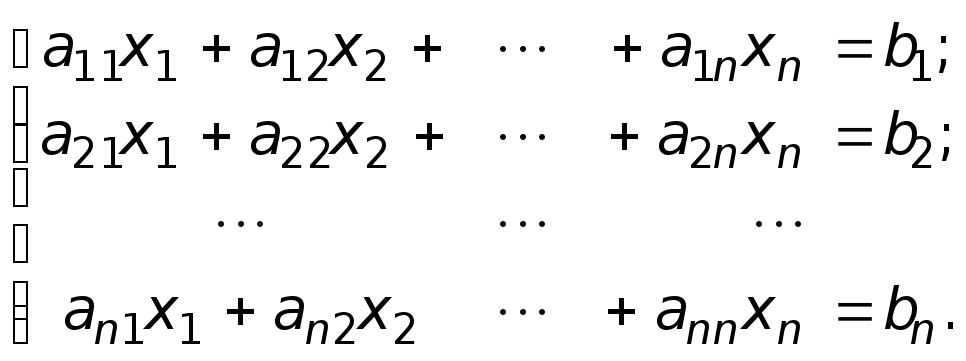 (2)
(2) .
.![]() – определитель, который получится из
определителя системы
– определитель, который получится из
определителя системы
![]() заменой j-го
столбца на столбец
заменой j-го
столбца на столбец![]() .
.![]() ,
то система имеет единственное
решение,
которое вычисляется по формулам
,
то система имеет единственное
решение,
которое вычисляется по формулам
![]() .
.
