
- •Содежание
- •Тема: Совместные исследования уравнения двух прямых
- •Тема: Не полное уравнение прямой
- •Тема: аналитическая геометрия в пространстве
- •Тема: Неполные уравнения плоскости
- •Тема: уравнение плоскости проходящей через три точки
- •Тема: Прямая в пространстве. Канонические и параметрические уравнения прямой.
- •Тема: уравнение прямой, проходящее через 2 точки
- •Тема: Прямая, как пересечение двух плоскостей
- •Тема: Параллельность и перпендикулярность двух плоскостей, двух прямых, прямой и плоскости.
- •Тема: Кривые второго порядка. Эллипс. Вывод канонического уравнения эллипса.
- •Тема: Исследование формы эллипса и его построения.
- •Тема: Эксцентриситет эллипса
- •Тема: Гипербола
- •Тема: Исследование уравнения гиперболы
- •Тема: Эксцентриситет гиперболы
- •Тема: Исследование формы параболы.
- •Тема: Матрица. Понятие матрицы. Основные определения.
- •Тема: Действие над матрицами
- •Тема: свойства умножения матриц
- •Тема: Обратная матрица и ее вычисление
- •Тема: Вычисление обратной матрицы
- •Тема: Решение систем линейных уравнений матричным способом
- •Тема: Дифференциальное исчисление
- •Тема: Неявные и обратные функции.
- •Тема: Понятие числовой последовательности и Эпсилон окрестности точки.
- •Тема: Понятие Эпсилон окружности точки.
- •Тема: Предел последовательности (числовой)
- •Тема: Предел функции
- •Односторонние пределы
- •Предел функции при бесконечном стремлении аргумента.
- •Тема: Не ограниченные и ограниченные функции
- •Тема: бесконечно малые величины и их свойства
- •Тема: Основные теоремы о пределах
- •Тема: Первый замечательный предел
- •Тема: второй замечательный предел. Число e, натуральные логарифмы
- •Тема: Сравнение бесконечно малых величин
- •Тема: Некоторые свойства непрерывной функции.
- •Тема: Условие непрерывности функции
- •Тема: Классификация точек разрыва
- •Тема: Производная и дифференциал
- •Тема: Определение производной ее геометрический и механический смысл.
- •Тема: Механический и геометрический смысл производной.
- •Тема: Дифференцируемость функции
- •Тема: Производные некоторых элементарных функций.
- •Тема: Понятие сложной функции и ее производная
- •Тема: Производная функций и
- •Тема: Производная неявно заданной функции
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА им. И.М. ГУБКИНА
ФИЛИАЛ В Г. ОРЕНБУРГЕ
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
Дубинкин А.В.
КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ
(линейная алгебра и аналитическая геометрия)
Методическое пособие
Оренбург 2008
Содежание
ВВЕДЕНИЕ
Данный курс лекций читался автором в течение многих лет в Оренбургском филиале РГУ нефти и газа им. И.М. Губкина для студентов вечерней формы обучения. В настоящее время, когда, кроме вечерней, возникла еще и заочная форма обучения, появилась необходимость в учебном пособии, содержание которого было бы согласовано с рабочей программой для студентов-заочников.
Распределение материала по семестрам полностью соответствует темам, указанным в учебном плане университета. Так как объем аудиторных часов на заочном отделении очень мал, то большое количество тем выносится на самостоятельное обучение, а темы, рассматриваемые в аудитории, излагаются кратко, почти в стиле справочника. Для более подробного знакомства с материалом необходимо использовать основную и дополнительную литературу, список которой прилагается в конце данного пособия.
Примеры, иллюстрирующие теоретический материал, приводятся здесь не везде. Однако их нехватку можно с избытком компенсировать примерами, имеющимися в предлагаемой литературе.
Теоретический материал, содержащийся в данном пособии, полностью соответствует программе 1 семестра.
Автор
Линейная алгебра
Элементы теории определителей
Определители 2-го порядка
О
дельта![]()
где
a ij – некоторые числа, называемые элементами определителя.
Элементы определителя, находящиеся на одной горизонтали, составляют строку. Элементы определителя, находящиеся на одной вертикали, составляют столбец. Число строк и столбцов всегда одинаково.
a21 – элемент определителя, который находится во второй строке и первом столбце.
Элементы, у которых номер строки равен номеру столбца, образуют главную диагональ определителя. Остальные элементы образуют побочную диагональ.
Пример: Вычислить определитель:
Величина
определителя![]()

Определители 3-го порядка
Определителем 3-го порядка называется число, имеющее вид квадратной таблицы, снабженной правилом вычисления.

![]()
![]()
Главная диагональ определителя состоит из всех элементов, у которых номер строки совпадает с номером столбца. Побочная диагональ состоит из элементов диагонали, перпендикулярной главной диагонали.
Вычисление определителя 3-го порядка (метод треугольников).
Сначала вычисляется произведение всех элементов главной диагонали. Затем к нему прибавляется произведение трёх элементов, стоящих в вершинах треугольника, одна сторона которого параллельна главной диагонали, а третья вершина находится в углу определителя по другую сторону главной диагонали. Затем прибавляется произведение трёх элементов, стоящих в вершинах треугольника, симметричного предыдущему треугольнику относительно главной диагонали. Далее прибавляются со знаком минус последние три члена определителя, полученные уже не с помощью главной, а с помощью побочной диагонали.
Пример: вычислить определитель
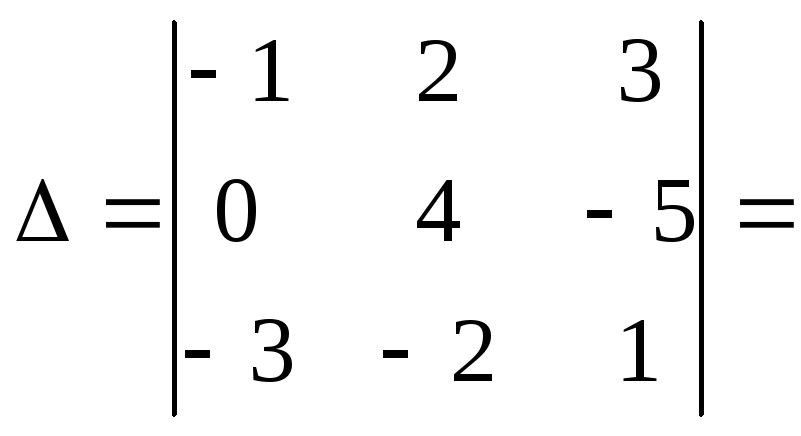
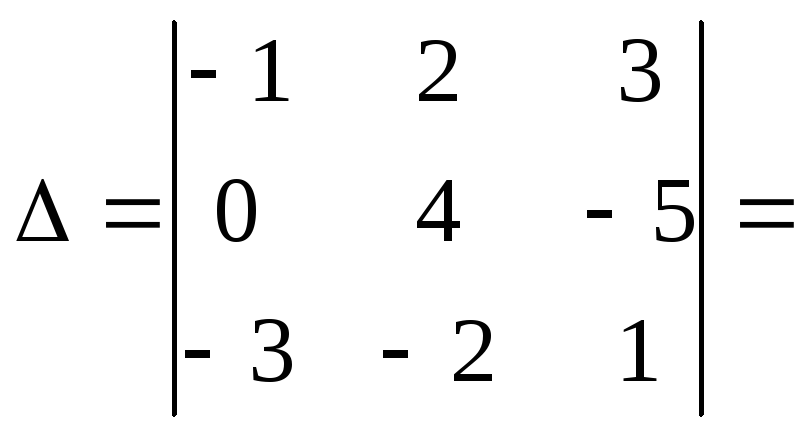





![]()
Величина
определителя![]()

М
Свойства определителей.
Свойства рассмотрим на примере определителей 3-го порядка.

1. Определитель не меняется при его транспонировании.
Транспонированием называется перемена местами строк и столбцов так, что столбец и строка с одинаковыми номерами меняются местами, при этом элементы главной диагонали определителя остаются на месте.
Доказывается непосредственным вычислением.
Следствие: строки и столбцы определителя равноправны. Это означает, что если какая-то теорема справедлива для строк, то она будет верна для столбцов и наоборот.

2. Если поменять местами любые две строки определителя, то его величина изменится на противоположную величину. Например, если величина определителя равна 5, то, поменяв, получим величину определителя равную –5.
Доказывается непосредственным вычислением.

3. Если определитель имеет две одинаковые строки, то он равен нулю. Доказывается непосредственным вычислением.

4. Умножение любой строки определителя на число k равносильно умножению всего определителя на это число k. Например, если величина определителя равна 5, а его строку умножают на 3, то весь определитель умножается на 3.
Доказывается непосредственным вычислением.

5. Строка называется нулевой, если она состоит из нулей. Если некоторая строка определителя – нулевая, то величина определителя = 0.
Доказывается непосредственным вычислением.

6. Две строки определителя называются пропорциональными, если элементы одной строки получаются из элементов второй строки умножением на одно и тоже число k. Если некоторые две строки определителя пропорциональны, то он равен 0.
Доказывается непосредственным вычислением.
7. Пусть каждый элемент некоторой строки определителя имеет вид суммы двух слагаемых. Тогда этот определитель равен сумме двух определителей, в первом из которых соответствующая строка состоит из первых слагаемых, а во втором определителе – из вторых слагаемых. Остальные элементы двух определителей такие же, как и в исходном определителе.
Доказывается непосредственным вычислением.

8. Если элементы некоторой строки определителя умножить на одно и тоже число k, и прибавить к соответствующим элементам другой строки, то величина определителя не изменится.
Доказывается непосредственным вычислением.
Разложение определителей по строке или столбцу. 9-е свойство определителей.
Распишем определитель 3-го порядка и сгруппируем его члены так, чтобы в каждом из двух членов присутствовал один и тот же элемент первой строки.
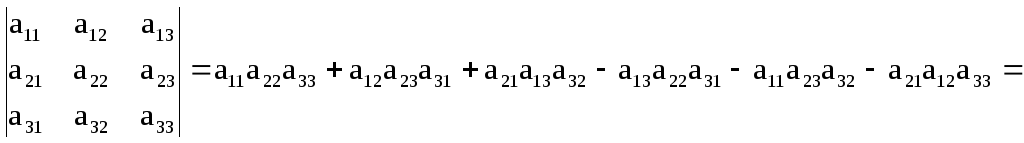












![]()
Это выражение называется разложением определителя по элементам первой строки.
Значения A11, A12, A13, называются алгебраическими дополнениями элементов первой строки. Аналогично можно получить разложение определителя по элементам любой строки или столбца.

9. Величина определителя равна сумме произведений элементов любой его строки на их алгебраические дополнения.
Доказывается непосредственным вычислением.
Алгебраические дополнения элементов определителя вычисляются следующим образом.
Пусть имеется aij (i = 1, 2, 3) (j = 1, 2, 3), нужно найти его алгебраическое дополнение.
Зачеркиваем ту строку и тот столбец определителя, на пересечении которых стоит этот элемент. Получим определитель второго порядка – Mij , который называется минором данного определителя третьего порядка, тогда справедлива формула:
Aij = (-1)I+j * Mij
I + j – сумма номеров зачеркнутой строки и столбца.
Н
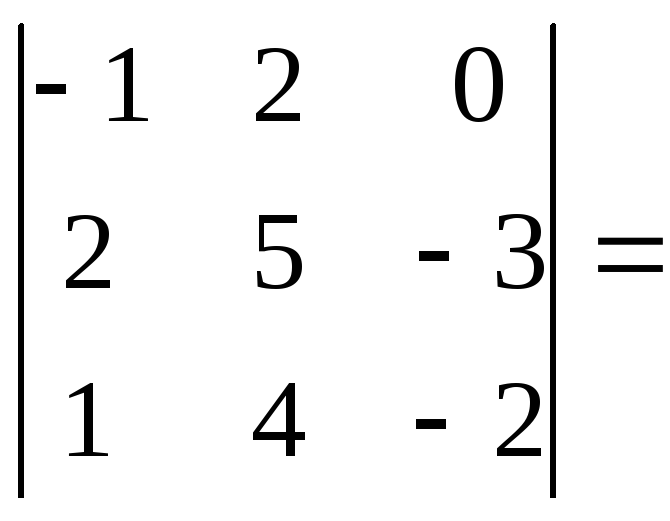
![]()
![]()
![]()
![]()
![]()

Замечание. Из 9-го свойства следует, что при разложении определителя по строке или столбцу, он выражается через несколько определителей, на единицу меньшего порядка. Например, определитель 4-го порядка выражается через четыре определителя 3-го порядка. Поэтому определитель любого порядка в принципе можно вычислить, выражая его через определители меньших порядков.
Решение системы двух линейных алгебраических уравнений с двумя неизвестными. Правило Крамера.
Система равенств вида:
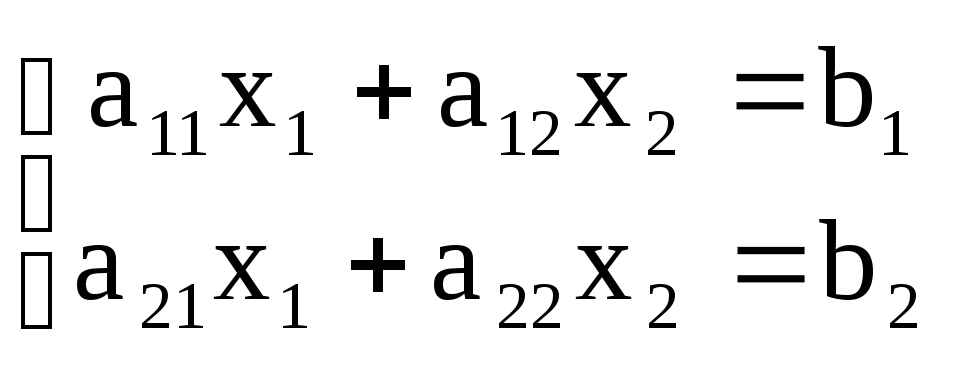
называется системой двух линейных алгебраических уравнений с двумя неизвестными.
Числа a 11 , a 12 , a 21 , a 22 называются коэффициентами при неизвестных;
x 1 , x 2 – неизвестные;
b 1 , b 2 – свободные члены.
Задача. Решить систему либо доказать ее несовместность.
Умножим первое уравнение системы на a22, а второе уравнение – на a12:

Вычитаем из верхнего уравнения нижнее.
![]()
![]() .
.
Теперь умножим верхнее уравнение на a21 , нижнее – на a1 :
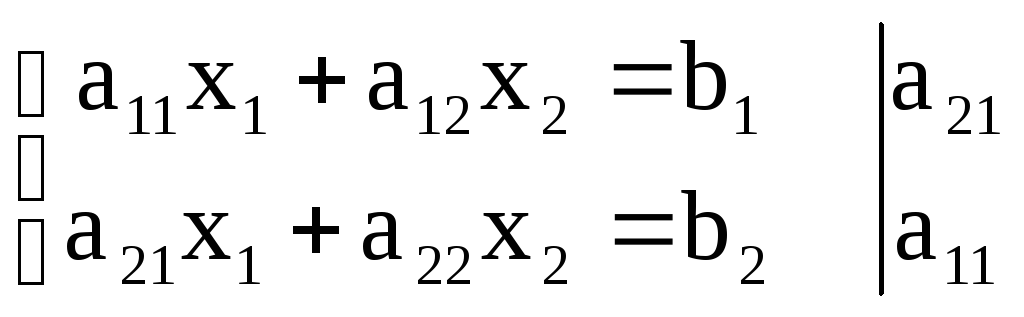
Вычитаем из нижнего уравнения верхнее.
![]()
![]() ,
,
где
![]()
Определитель второго порядка, составленный из коэффициентов при неизвестных, называется определителем системы или главным определителем.
![]() – первый побочный
определитель.
– первый побочный
определитель.
![]() – второй побочный
определитель.
– второй побочный
определитель.
![]()
![]() – формулы
Крамера.
– формулы
Крамера.
1-й случай 0
![]()
![]() .
.
Формулировка теоремы:
Если определитель системы двух линейных алгебраических уравнений с двумя неизвестными отличен от 0 или 0, то данная система имеет решение и при том единственное, определяемое формулой Крамера.
Теорема Крамера и формулы Крамера дают правило (алгоритм) решения системы двух линейных уравнений с двумя неизвестными.
2-й случай =0
![]()
![]()
а) хотя бы один из побочных определителей не равен 0, тогда хотя бы одно из этих двух равенств является противоречивым. Следовательно, система не имеет решений (система несовместна).
б) оба побочных определителя равны 0, тогда
![]()
![]()
В этом подслучае система имеет бесчисленное множество решений.
Упорядоченные множества чисел.
Пусть дана система двух линейных алгебраических уравнений с двумя неизвестными, и пусть определитель системы не равен нулю(0), тогда по теореме Крамера система имеет решение, и притом единственное. Пусть x 1 и x 2 – это числа, составляющие решение системы.
Составим из этих чисел пару, в которой x1 находится слева а x2 – справа
(x1; x2), тогда эта пара чисел называется упорядоченной парой или упорядоченной двойкой чисел.
Так как пара одна, то решение системы одно.
Пример:
(3;5)
x1 = 3
x2 = 5
(5;3)
x 1 = 5
x 2 = 3
В упорядоченной двойке менять местами числа нельзя, так как это приведет к другой упорядоченной двойке.
Теорема Крамера для системы трех линейных алгебраических уравнений с тремя неизвестными.
Система вида:
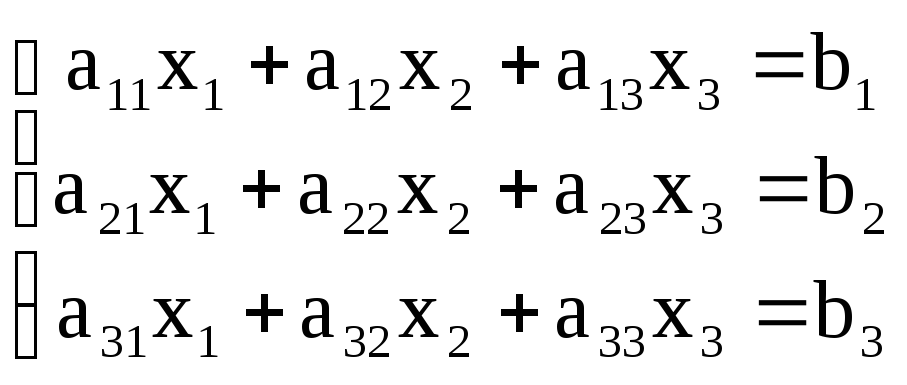
называется системой трех линейных алгебраических уравнений с тремя неизвестными.
Числа a11 , … называются коэффициентами при неизвестных;
x1, … – неизвестные;
b1, … – свободные члены.
Рассмотрим главный определитель системы (определитель, составленный из коэффициентов при неизвестных):

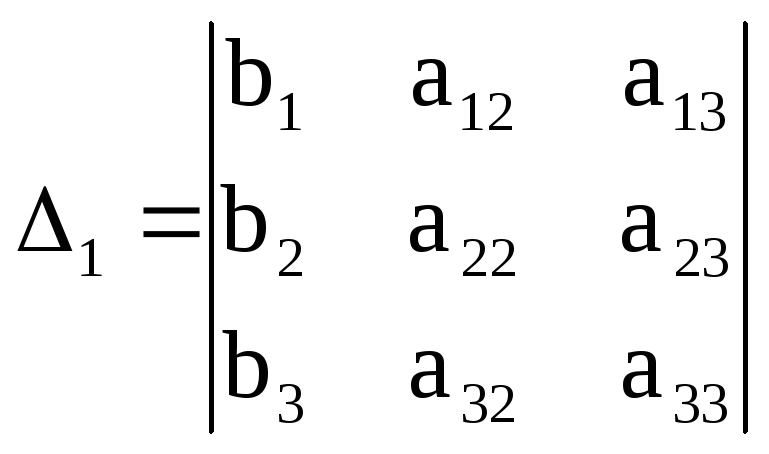
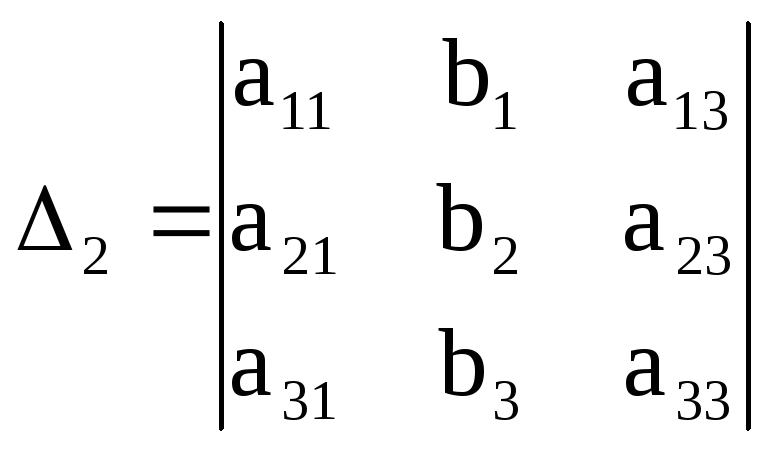
 .
.
Теорема Крамера. Если определитель системы отличен от нуля, то система имеет решение и притом единственное, определяемое формулами Крамера:
![]() ;
;
![]() ;
;
![]() .
.
Правило Крамера – это метод (алгоритм) решения системы трех линейных уравнений с тремя неизвестными в случае ненулевого определителя системы.
Пример. Дана система:

Найти все её решения или доказать её несовместность. Найдем определитель этой системы:

Определитель системы равен 33, то есть оказался отличным от 0. Следовательно, система имеет решение и притом единственное.
Вычислим теперь побочные определители:
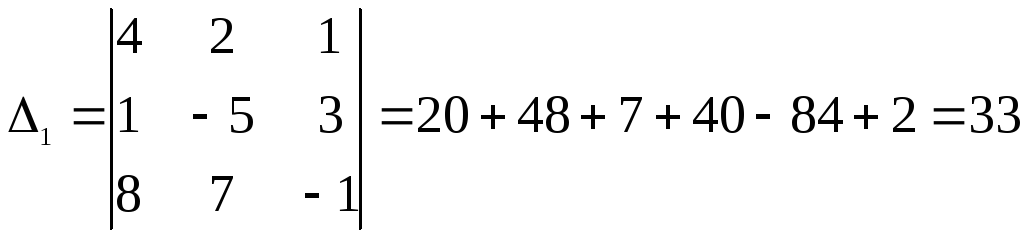
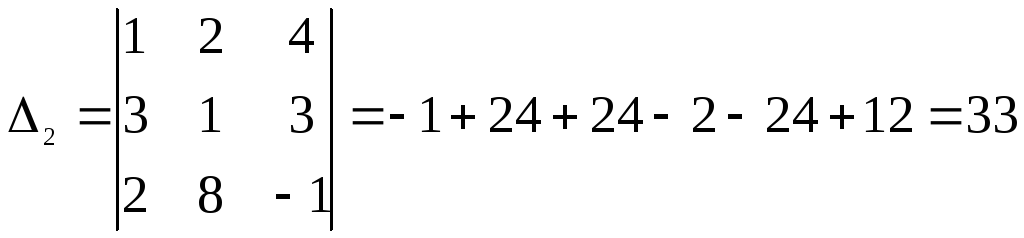
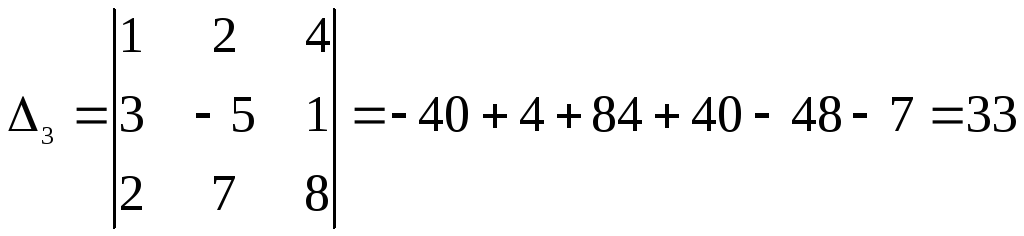
Теперь найдем решение по формулам Крамера:
![]() ,
,
![]() ,
,
![]() .
.
Проверка:
![]()
![]()
![]()
Ответ:
![]() .
.
Декартовы прямоугольные системы координат на плоскости и в пространстве.
-
(x1,y1,z1), В пространстве.
Декартовой прямоугольной системой координат в пространстве называется множество из трех взаимно перпендикулярных числовых осей, пересекающихся в одной точке, имеющих единый масштаб и каким-либо образом перенумерованных (ДПСК).
 z
z
 M3
M3

 x0
M
x0
M
y0 0 M2 y



1
 M1
M11
M1
M11
x
z0
Координатные оси называются: ох – ось абсцисс, оу – ось ординат, oz – ось аппликат. Точка О называется началом координат. Плоскости xоy, xоz, yоz называются координатными плоскостями.
Рассмотрим точку М.
Длины отрезков ОМ1; ОМ2; ОМ3, взятые с соответствующими знаками называются декартовыми прямоугольными координатами точки М: М(x0;y0;z0)
Вывод: каждой точке пространства соответствует упорядоченная тройка чисел, называемых ее координатами.
Решим обратную задачу:
Пусть
имеется произвольная упорядоченная
тройка чисел. Соответствуют ли этой
тройке точки пространства, если да, то
сколько?![]()
![]()
 z
z
 z1
z1
M(x1; y1; z1)
 0
y
0
y




 x1
M1
x1
M1
x
На оси оx от начала координат отложим число, являющееся первым числом упорядоченной тройки. На осях оy и оz отложим соответственно второе и третье числа этой тройки. Затем сделаем построения как показано на чертеже. Получили точку М, единственную точку пространства, координаты которой совпадают с соответствующими числами данной упорядоченной тройки.
Вывод. Любой упорядоченной тройке чисел в ДПСК принадлежит единственная точка пространства, координаты которой и есть числа заданной тройки.
Обе теоремы можно объединить:
Между точками пространства и упорядоченными тройками чисел существует взаимно однозначное соответствие.
Одной точке соответствует одна тройка, одной тройке соответствует одна точка.
2)На плоскости.
ПДСК на плоскости называется две взаимно перпендикулярные оси каким-либо образом перенумерованные и снабженные единым масштабом.
y

 b
M(a;
b)
b
M(a;
b)


0 1 a x
Между точками плоскости и упорядоченными парами чисел существует взаимно однозначное соответствие.
Векторы
Понятие свободного вектора. Основные определения.
Физические величины подразделяются на:
1) Скалярные (характеризуются численными значениями, например, длина, плотность и т.д.)
2) Векторные (скорость точки, ускорение, сила и т.д.) – величина, которая задается не только числовым значением, но и направлением.
А – начальная точка отрезка
В
– начальная точка отрезка
В
В – конечная точка отрезка А
На данном отрезке задано направление от точки А к точке В, т.е отрезок стал направленным, такие отрезки называются векторами.
Определение: Вектор – направленный отрезок.
Обозначают вектор: AB, a.
Длина отрезка АВ называется длиной вектора AB или его модулем.
Начальная точка вектора называется точкой его приложения.
Существует несколько основных видов векторов:
1) Свободный – начальную точку вектора можно перенести в любую точку пространства;
2) Скользящий – начальную точку вектора можно перенести в любую точку прямой, которой принадлежит этот вектор;
3) Связанный – начальную точку вектора переносить нельзя.
Будем изучать в дальнейшем только свободные векторы. Два вектора равны друг другу, если они имеют одну и ту же длину и одно и то же направление:
![]() .
Если начальная точка вектора совпадает
с его конечной точкой, то такой вектор
называется нулевым или ноль-вектором.
Два вектора, имеющие одинаковые длины,
но противоположно направленные,
называются противоположными векторами.
.
Если начальная точка вектора совпадает
с его конечной точкой, то такой вектор
называется нулевым или ноль-вектором.
Два вектора, имеющие одинаковые длины,
но противоположно направленные,
называются противоположными векторами.
Радиус-вектором точки М называется вектор, начало которого совпадает с началом координат, а конец – с точкой М.
Проекция вектора на ось.

 В
В
![]()




 А
С
А
С

А1 В1 L
Алгебраической проекцией (или просто проекцией) вектора АВ на ось L называется длина отрезка А1В1, взятая с соответствующим знаком.
А1В1
– проекция
на ось L
вектора
![]() .
Вычислим длину этой проекции. Для этого
рассмотрит треугольник ABC:
АС=
.
Вычислим длину этой проекции. Для этого
рассмотрит треугольник ABC:
АС=![]() .
Так как А1В1
= AC,
то длина проекции найдена.
.
Так как А1В1
= AC,
то длина проекции найдена.
Два ненулевых вектора называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Из этого определения следует, что коллинеарные векторы могут быть либо одинаково направлены, либо противоположно направлены. Другие варианты взаимного расположения коллинеарных векторов отсутствуют.
Координаты вектора.
Существуют два способа задания векторов:
1) Геометрический (вектор изображается направленным отрезком),
2) Координатный (аналитический).
 z
z
![]()


 M
M
γ
 az
az

β



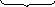 0
у
0
у
 aу
aу
ах
Проекция вектора на координатную ось называется его координатой на этой оси.
Наличие
у координатных осей порядковых номеров
означает, что и координаты вектора также
имеют порядковые номера. Поэтому, они
могут быть записаны в виде упорядоченной
тройки
![]() .
Координаты вектора выражаются через
его модуль и косинусы углов между
направлением вектора и положительным
направлением координатной оси по
формулам:
.
Координаты вектора выражаются через
его модуль и косинусы углов между
направлением вектора и положительным
направлением координатной оси по
формулам:
![]()
![]()
![]()
Cos![]() ,
cos
β,
cos
– направляющие cos
вектора
,
cos
β,
cos
– направляющие cos
вектора
![]() .
.
Теорема: Координаты вектора равны разностям соответствующих координат его конца и его начала.
Доказательство:
![]()


А

х1 ах х

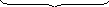
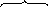
0 А1 Х2 В1
![]()
Тогда, если в пространстве задан вектор АВ и координаты точки
А
(х1,у1,z1),
а также координаты точки В (х2,у2,z2),
то:
![]() х
= х2–х1,
х
= х2–х1,
![]() у
= у2–у1,
у
= у2–у1,
![]() z
= z2–z1.
z
= z2–z1.
Направляющие косинусы вектора

 z
z
M3
 ay
М
ay
М
![]()


 0
az M2
y
0
az M2
y



ax M
 M1
M´
M1
M´
x
М´М1 ОХ по построению.
ММ1 – наклонная, проекция которой М´М1. Тогда по теореме обратной теореме о трех перпендикулярах, ММ1ох
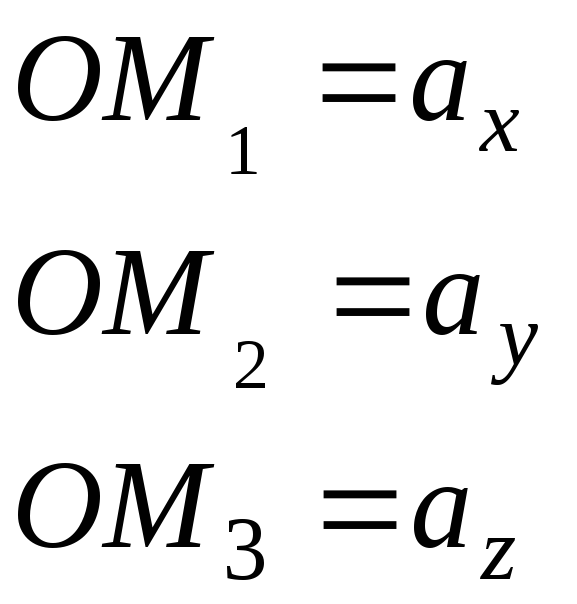
Тогда
по теореме Пифагора квадрат длины
![]()
|a|² = (ОM1)² + (ОM2)² + (ОM3)².
Тогда
|![]() |²
= a²x+
a²y+ a²z,
|²
= a²x+
a²y+ a²z,
![]()
Выразим направляющие косинуса вектора через его координаты.
![]()
cos![]()
![]()
![]()
Возведем в квадрат обе части трех последних равенств и почленно сложим их
![]()
![]() =1
– условие,
связывающее направляющие косинусы
вектора.
=1
– условие,
связывающее направляющие косинусы
вектора.
Расстояние между двумя точками.
Рассмотрим в пространстве две различные точки, заданные своими координатами
М1 (х1;у1;z1)
М2 (х2;у2;z2)
 d
M2
d
M2
M1
Введем
вектор
![]() :
:
![]()
Расстояние
между М1
и М2
это модуль вектора
![]()
![]() – расстояние
между двумя точками М1
и М2 в
пространстве.
– расстояние
между двумя точками М1
и М2 в
пространстве.
Замечание: Приведем без доказательства аналогичные формулы для случая плоскости
М (ОМ1;ОМ2)
![]()

![]()
![]()
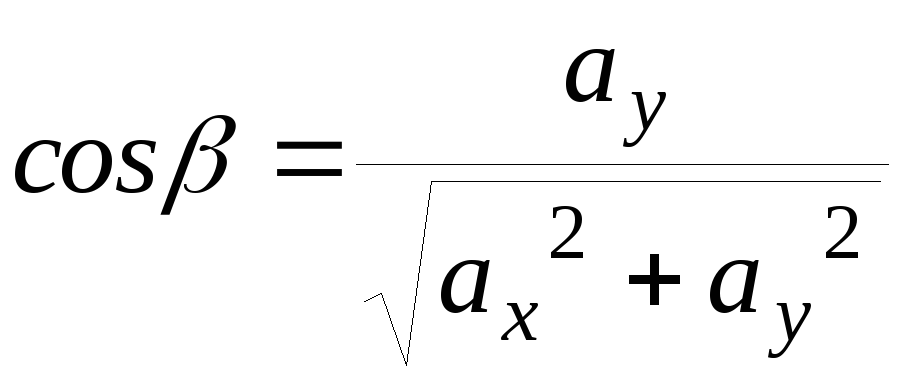
![]() –
расстояние
между двумя точками на плоскости.
–
расстояние
между двумя точками на плоскости.
Линейные операции над векторами.
-
Сложение векторов
Суммой
векторов
![]() и
и
![]() называется такой вектор
называется такой вектор
![]() ,
величина и направление которого
определяется по правилу треугольника:
,
величина и направление которого
определяется по правилу треугольника:
Правило треугольника:
![]()


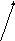
![]()
![]()
Тогда
вектор
![]() – это
вектор, начало которого совпадает с
началом первого вектора, а конец –с
концом второго вектора.
– это
вектор, начало которого совпадает с
началом первого вектора, а конец –с
концом второго вектора.
Замечание: Это правило можно рассматривать на случай более чем двух слагаемых, оно называется правилом n- угольника:
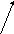

![]()

![]()

![]()
![]()

![]()
![]()
Свойства операции сложения вектора.
1)
![]() переместительность (коммутативность)
переместительность (коммутативность)
2)
![]() сочетательность (ассоциативность)
сочетательность (ассоциативность)
2. Вычитание векторов.
Разностью
векторов
![]() и
и
![]() называется
такой вектор
называется
такой вектор
![]() ,
который, будучи сложен с вектором
,
который, будучи сложен с вектором
![]() дает в сумме вектор
дает в сумме вектор
![]() :
:


![]()
![]()

![]()
3.Умножение вектора на число.
Пусть дан вектор
![]() и число .
Произведением вектора
и число .
Произведением вектора
![]() на число
называется такой вектор
на число
называется такой вектор
![]() ,
длина которого равна
,
длина которого равна
![]() ,
а направление совпадает с направлением
вектора
,
а направление совпадает с направлением
вектора
![]() ,
если >0
или противоположно направлению вектора
,
если >0
или противоположно направлению вектора
![]() ,
если <0.
,
если <0.
Замечание: если
=0,
то
![]() ,
т.е. 0·
,
т.е. 0·![]() =
=![]() направление которого не определено (0-
вектор).
направление которого не определено (0-
вектор).
С геометрической
точки зрения умножение
![]() на
есть «растяжение» вектора а в
раз, если
>1
и
«сжатие»
в
раз, если 1>>0.
на
есть «растяжение» вектора а в
раз, если
>1
и
«сжатие»
в
раз, если 1>>0.
Свойства операций умножения вектора на число.
1)
![]() (распределительность
относительно векторного множителя),
(распределительность
относительно векторного множителя),
2)
![]() (ассоциативность относительно числового
множителя),
(ассоциативность относительно числового
множителя),
3)![]() (распределительность
относительно числового множителя).
(распределительность
относительно числового множителя).
Следствия из определения линейных операций
Рассмотрим
![]() ·(-1)=
·(-1)=![]()
![]()
Направление
![]() -будет
противоположно
-будет
противоположно
![]()
Длина
![]() =
=![]()
(-1)·
![]() =
-
=
-![]()
Также
как в арифметике существуют противоположные
числа, в векторной алгебре существуют
противоположные вектора -![]() называется противоположным
называется противоположным
![]()
![]()
Рассмотрим
два произвольных вектора
![]() и
и
![]()
Рассмотрим
векторное выражение
![]()
Так как сложение векторов подчиняется закону переместительности и сочетательности
![]()
![]()
Два вектора называются коллинеарными, если они расположены на параллельных прямых либо на одной прямой. Из определения следует, что коллинеарные векторы либо сонаправлены (одинаково), либо противоположно направлены. Поэтому результатом умножения на число, всегда является вектор коллинеарный первоначальному.
![]()
![]()
![]()
![]()
Теоремы о проекциях вектора на ось.
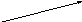
Первая теорема. Рассмотрим векторы AB, BC и их сумму AC. Спроектируем все векторы на ось L:
 В
В
![]()

 С
С

![]()
 А
А
 L
L
А´ В´ С´
![]() –
проекция вектора
–
проекция вектора
![]() на ось L;
на ось L;
![]() –
проекция вектора
–
проекция вектора
![]() на ось L;
на ось L;
![]() –
проекция вектора
–
проекция вектора
![]() на ось L.
на ось L.
![]()
Проекция
вектора![]() равна проекции
равна проекции
![]() + проекция
+ проекция
![]() .
.
Теорема:
Проекция суммы двух векторов на ось L равна сумме проекций слагаемых векторов на эту ось.
Вторая
теорема.
Пусть дан вектор AB
и число .
Спроектируем вектор AB
и его произведение на число ,
то есть вектор AC
на ось L.
Из чертежа видно, что
![]() =
=
![]() • .
• .
C
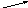

![]() B
B



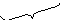 A
λ
A
λ![]()
Приходим
к теореме: Проекция произведения
![]() на
равна произведению
на проекцию
на
равна произведению
на проекцию
![]() .
.
Условие коллинеарности двух векторов в координатах.
Теорема:
Чтобы
два вектора
![]() и
и
![]() были коллинеарными необходимо и
достаточно, чтобы выполнялось равенство
были коллинеарными необходимо и
достаточно, чтобы выполнялось равенство
![]() =
=
![]()
-
Необходимость.
Пусть
векторы
![]() и
и
![]() коллинеарны. Это значит, что они либо
сонаправлены, либо противоположно
направлены. А это означает, что
коллинеарны. Это значит, что они либо
сонаправлены, либо противоположно
направлены. А это означает, что
![]() можно представить как
можно представить как
![]() ,
умноженный на подходящее число :
,
умноженный на подходящее число :
![]() =
=![]() .
.
-
Достаточность
Пусть
![]() и
и
![]() связаны равенством
связаны равенством ![]() =
=![]() .
Это означает, что вектор
.
Это означает, что вектор
![]() есть произведение
есть произведение
![]() на .
Из определения операции умножения
вектора на число следует, что
на .
Из определения операции умножения
вектора на число следует, что
![]() либо сонаправлен, либо противоположно
направлен
либо сонаправлен, либо противоположно
направлен
![]() ,
т.е. они коллинеарны. Теорема доказана.
,
т.е. они коллинеарны. Теорема доказана.
Рассмотрим запись коллинеарности в координатах.
Из определения координат вектора следует, что два вектора заданные своими координатами равны друг другу тогда и только тогда, когда равны их соответствующие координаты
![]() ,
,
![]()
 Вывод:
два вектора коллинеарны тогда и только
тогда, когда их координаты пропорциональны.
Вывод:
два вектора коллинеарны тогда и только
тогда, когда их координаты пропорциональны.
Линейные операции в координатах.
-
Сложение векторов.
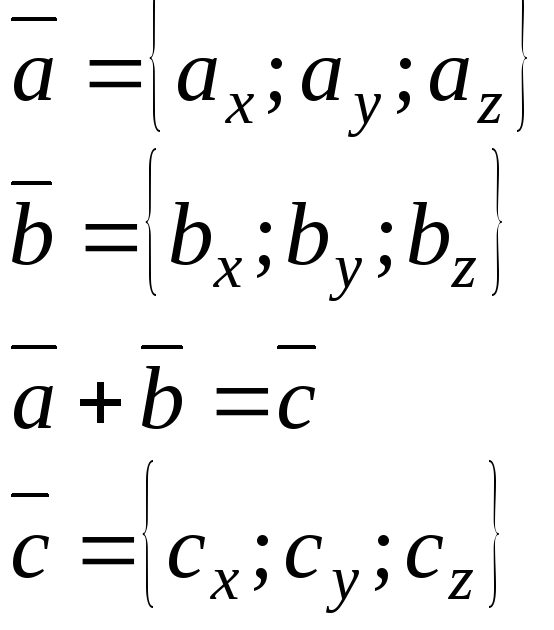
По первой теореме о проекциях можно записать равенство.
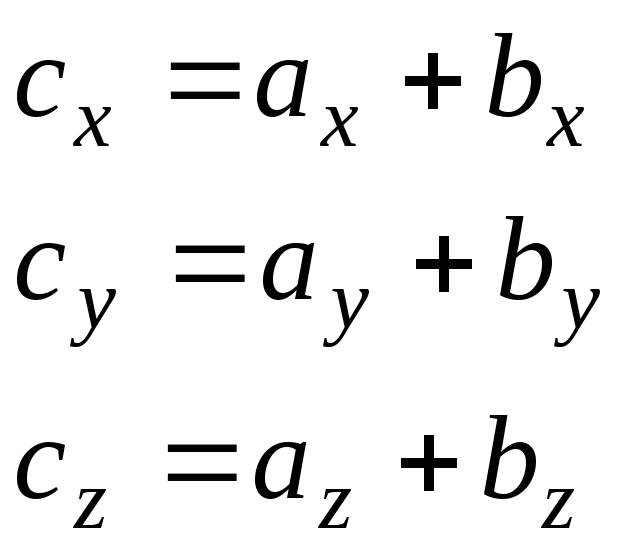
Координаты суммы двух векторов равны сумме соответствующих координат слагаемых векторов.
-
Вычитание векторов.
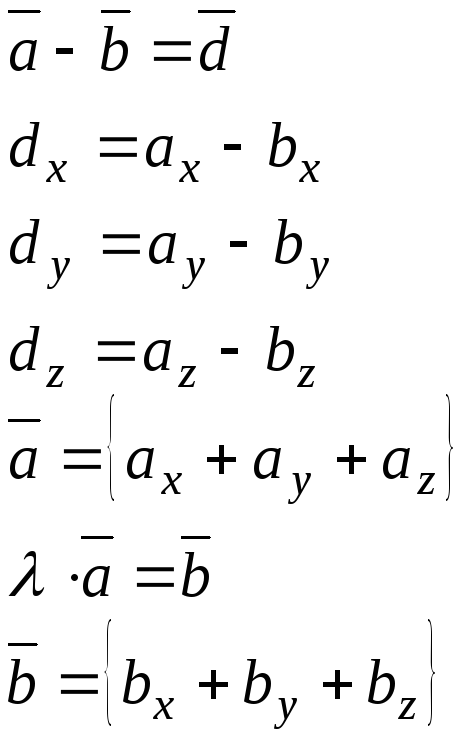
По второй теореме о проекциях вектора на ось приходим к равенствам

Вывод:
Координаты произведения
![]() на
равны произведениям соответствующих
координат
на
равны произведениям соответствующих
координат
![]() на это число .
на это число .
Понятие базиса в пространстве и на плоскости. Разложение вектора по базисным ортам.
1) В пространстве.
Рассмотрим в пространстве в прямоугольной декартовой системе координат три взаимно перпендикулярных вектора, каждый из которых направлен вдоль соответствующей координатной оси. Пусть длина каждого из этих векторов равна 1, а их начала совпадают с началом координат. Так как координатные оси перенумерованы, то оказываются перенумерованными и эти векторы. Такая тройка векторов называется согласованной с прямоугольной декартовой системой координат.
 z
z
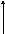
![]()

0 y



![]()
![]()
x
- упорядоченная
тройка
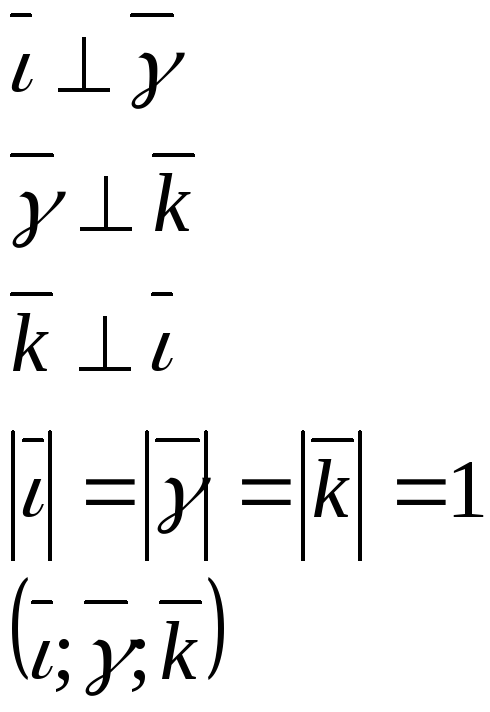
Базисом
в пространстве согласованным с ПДСК
называется упорядоченная тройка
единичных взаимно перпендикулярных
векторов
![]() .
.
Всякий единичный вектор называется орт, поэтому векторы базиса называются базисными ортами.
2) На плоскости.
Рассмотрим на плоскости в ПДСК два взаимно перпендикулярных орта, направленных вдоль координатных осей. Обозначим их i и j.
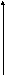 y
y
![]()
0

![]() x
x
Базисом
на плоскости называется упорядоченная
пара векторов
![]() и
и
![]() единичных и взаимно перпендикулярных.
единичных и взаимно перпендикулярных.
Выразим произвольный вектор a в пространстве через базисные орты.
Рассмотрим ПДСК в пространстве и произвольный вектор a, начало которого совпадает с началом координат:
 z
z
![]()

![]()

![]()
 0
0
![]()
![]() y
y





![]()
![]()

![]()
Рассмотрим
в пространстве произвольный
![]() .
Так как это свободный вектор, поместим
его начало в начало координат. Разложим
его на составляющие векторы по правилу
параллелограмма. По правилу параллелограмма:
.
Так как это свободный вектор, поместим
его начало в начало координат. Разложим
его на составляющие векторы по правилу
параллелограмма. По правилу параллелограмма:
![]() =
=![]() .
Разложим
.
Разложим
![]() на составляющие векторы вдоль осей ох
и оу
на составляющие векторы вдоль осей ох
и оу
![]()
![]()
Рассмотрим каждый из этих векторов.
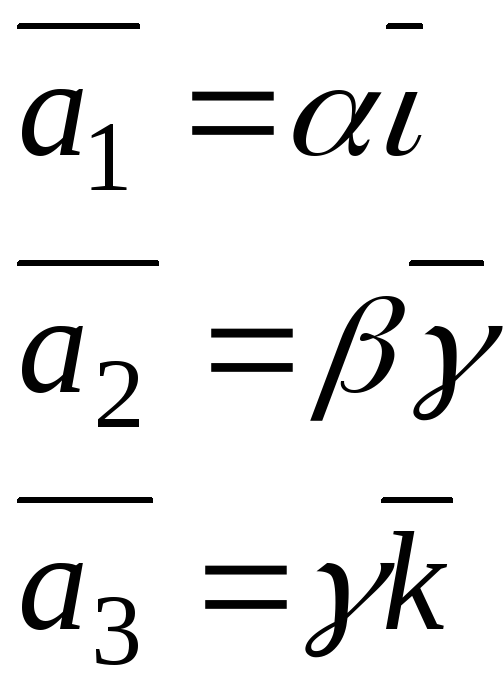
Тогда
![]() ,
где
,
где
![]() -
некоторые коэффициенты.
-
некоторые коэффициенты.
Выясним
геометрический смысл чисел
![]() .
Тогда по теореме обратной теореме о
трех перпендикулярах, эта наклонная
тоже перпендикулярна ох. Тогда модуль
вектора
.
Тогда по теореме обратной теореме о
трех перпендикулярах, эта наклонная
тоже перпендикулярна ох. Тогда модуль
вектора
![]() -
проекция на ось ох
-
проекция на ось ох
![]()
![]() (х – координата вектора
(х – координата вектора
![]() ).
С другой стороны
).
С другой стороны
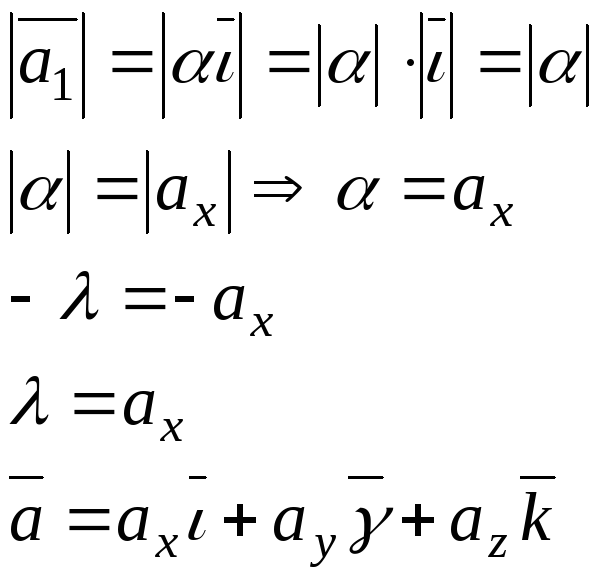
Теорема:
Любой
вектор пространства может быть представлен
в виде
![]() ,
где
,
где
![]() -
его координаты.
-
его координаты.
Замечание:
Выражение вектора через координаты:
![]() и доказанное равенство равносильны или
эквивалентны.
и доказанное равенство равносильны или
эквивалентны.
Скалярное произведение векторов.
Скалярным
произведением
![]() называется число являющееся произведением
называется число являющееся произведением
![]() умноженным на косинус угла между ними:
умноженным на косинус угла между ними:
![]() =
=![]() ·
cos
·
cos
![]()
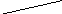

φ
![]()
![]() =
=![]()
Механический смысл скалярного произведения.
Пусть материальная точка прямолинейно движется из пункта A в пункт B. Пусть на нее действует сила F, постоянная по величине и направлению и составляющая угол φ с вектором перемещения. Вычислим работу этой силы по перемещению материальной точки из пункта A в пункт B.
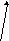


![]() B
B
φ
![]()
A
F- постоянная по величине и направлению сила, действующая на точку А,
![]() -
вектор перемещения (это вектор, начало
которого лежит в начальной точке, а
конец в конечной точке пути).
-
вектор перемещения (это вектор, начало
которого лежит в начальной точке, а
конец в конечной точке пути).
![]()
Вывод: Механический смысл скалярного произведения.
Если на прямолинейно движущуюся материальную точку действует постоянная сила F, то А этой силы численно равна скалярному произведению вектора этой силы на вектор перемещения материальной точки.
Свойства скалярного произведения.
а) алгебраические свойства:
1. Переместительность (не зависит от порядка умножения векторов)
![]()
2. Сочетательность (ассоциативность)
![]()
3.Распределительность
![]()
б) геометрические свойства:
1.
Если
![]() .
.
2.
Если
![]() .
.
3.
Если скалярное произведение двух
ненулевых векторов равно 0, то векторы
перпендикулярны, т.е.
![]() .
.
4. Если два не нулевых вектора взаимно перпендикулярны, то их скалярное произведение равно 0.
Объединим 3 и 4 свойства. Скалярное произведение двух ненулевых векторов равно 0 тогда и только тогда, когда они взаимно перпендикулярны.
5.Рассмотрим скалярное произведение вектора на самого себя:
![]()
Скалярное произведение в координатах.
Пусть дан
![]()
Задача: Выразить их скалярное произведение через их координаты:
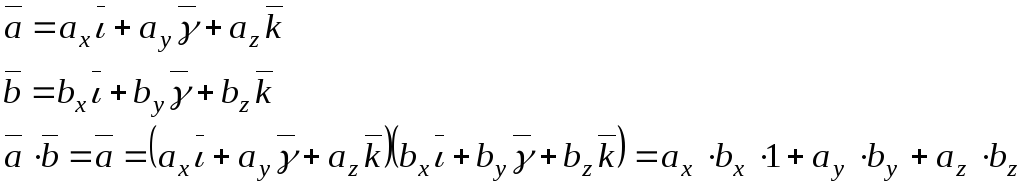
Если два вектора заданы своими координатами, то их скалярное произведение равно сумме произведений их соответствующих координат.
Задача: Выразим cos угла между векторами через их координаты:
![]()
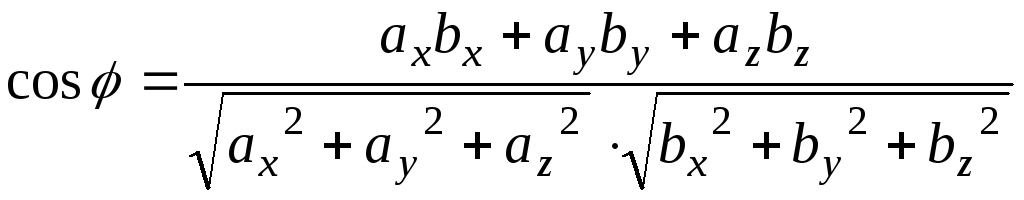
Найдем условие перпендикулярности двух векторов в координатах.
Условие
перпендикулярности двух векторов в
координатах![]()
Векторное произведение векторов.

![]()



φ

![]()
Векторным
произведением векторов
![]() и
и
![]() называется вектор
называется вектор
![]() ,
удовлетворяющий двум условиям:
,
удовлетворяющий двум условиям:
1)
длина этого вектора определяется
формулой:
![]() ,
,
2)
вектор
![]() перпендикулярен плоскости , содержащей
векторы
перпендикулярен плоскости , содержащей
векторы
![]() и
и
![]() и направлен так, что если смотреть с
конца вектора
и направлен так, что если смотреть с
конца вектора
![]() на эту плоскость, то кратчайший поворот
от
на эту плоскость, то кратчайший поворот
от
![]() к
к
![]() совершается против часовой стрелки.
совершается против часовой стрелки.
Обозначают
векторное произведение:
![]()
![]()
![]() ,
[
,
[![]()
![]() ],
(
],
(![]()
![]()
![]() ).
).
Геометрический и механический смысл векторного произведения.
-
Геометрический смысл.
Пусть имеются два
вектора
![]() и
и
![]() .
Построим эти векторы выходящими из
одной точки. Построим параллелограмм
на этих двух векторах. Тогда
.
Построим эти векторы выходящими из
одной точки. Построим параллелограмм
на этих двух векторах. Тогда


![]()


 φ
φ
![]()
площадь этого
параллелограмма вычисляется по формуле
S
=![]() .
Но так же определяется и модуль векторного
произведения этих векторов.
.
Но так же определяется и модуль векторного
произведения этих векторов.
Вывод: Модуль
векторного произведения
![]() и
и
![]() равен площади параллелограмма,
построенного на этих векторах как на
сторонах.
равен площади параллелограмма,
построенного на этих векторах как на
сторонах.
-
Механический смысл.
Рассмотрим в прямоугольной декартовой системе координат (ПДСК) в пространстве точку М. Пусть на нее действует сила F.
 z
z


![]()
 M
M

 0
y
0
y
x
Пусть
![]() – момент силы F.
По определению
– момент силы F.
По определению
![]() .
.
Вывод: Если на движущуюся в пространстве материальную точку М действует сила F, то момент этой силы равен векторному произведению радиуса вектора этой точки на вектор силы.
Свойства векторного произведения.
А) Геометрические свойства:
-
Если два ненулевых вектора коллинеарны, то их векторное произведение равно нулевому вектору.
-
Если векторное произведение двух ненулевых векторов равно нулевому вектору, то эти векторы коллинеарны:
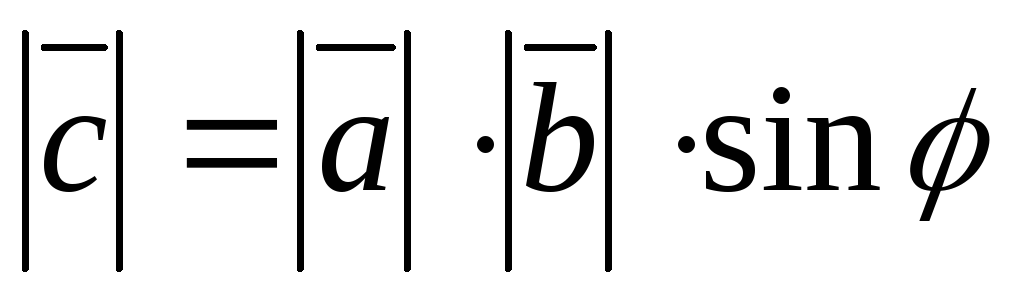 .
.
Из формулы видно,
что если |![]() |
= 0, то это возможно только тогда, когда
sin
φ
= 0. А из этого
условия вытекает, что φ
= 0° или φ=
180°. Значит векторы
|
= 0, то это возможно только тогда, когда
sin
φ
= 0. А из этого
условия вытекает, что φ
= 0° или φ=
180°. Значит векторы
![]() и
и
![]() либо сонаправлены, либо направлены
противоположно друг другу, то есть
коллинеарны.
либо сонаправлены, либо направлены
противоположно друг другу, то есть
коллинеарны.
Б) Алгебраические свойства:
-
Антикоммутативность (антипереместительность):
![]()
-
Ассоциативность (сочетательность):
![]()
-
Дистрибутивность (распределительность):
![]()
Векторное произведение в координатах.
Задача: Пусть два вектора заданы своими координатами. Нужно выразить их векторное произведение через их координаты.

Составим таблицу векторного умножения базисных ортов.

![]()

![]()



![]()
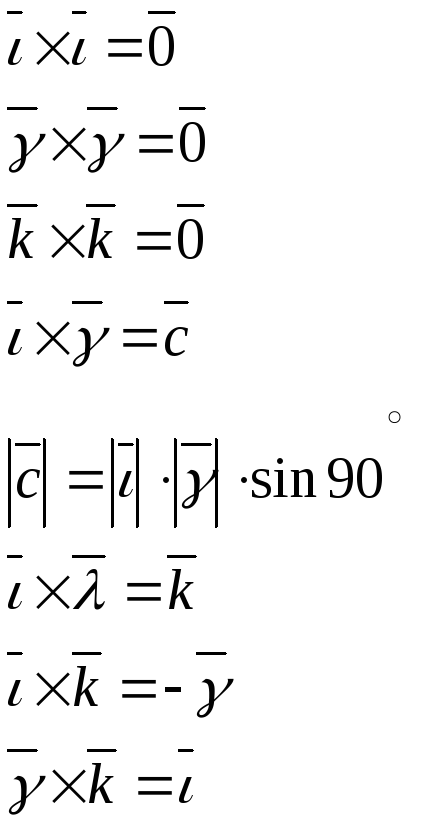
Получили таблицу векторного умножения базисных ортов. По распределительному свойству векторного произведения можно каждый член первой скобки умножить на каждый член второй скобки:
![]()
![]()
![]() =
=
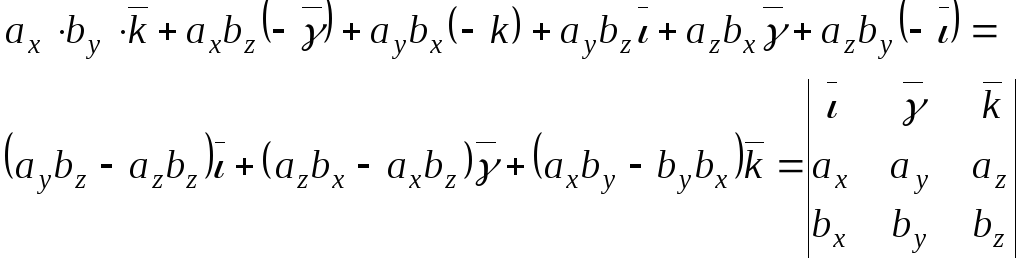
Вывод: Если два вектора заданы своими координатами в ПДСК, то вектор произведения первого на второй равен определителю третьего порядка, в первой строке которого стоят базисные орты, во второй – координаты первого вектора, а в третьей – координаты второго вектора.
Пример №1. В пространстве даны А (1;1;1), В (2;2;2), С (4;3;5). Найти площадь треугольника ABC.
Будем решать эту задачу, пользуясь формулой векторного произведения в координатах. Найдем сначала координаты векторов АВ и АС.
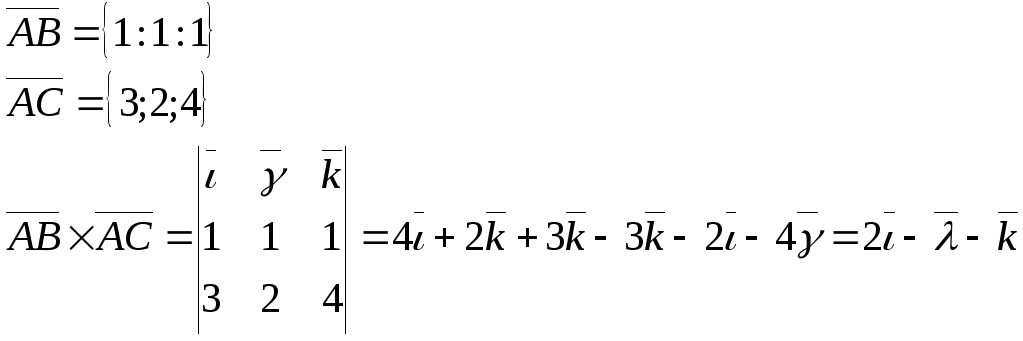
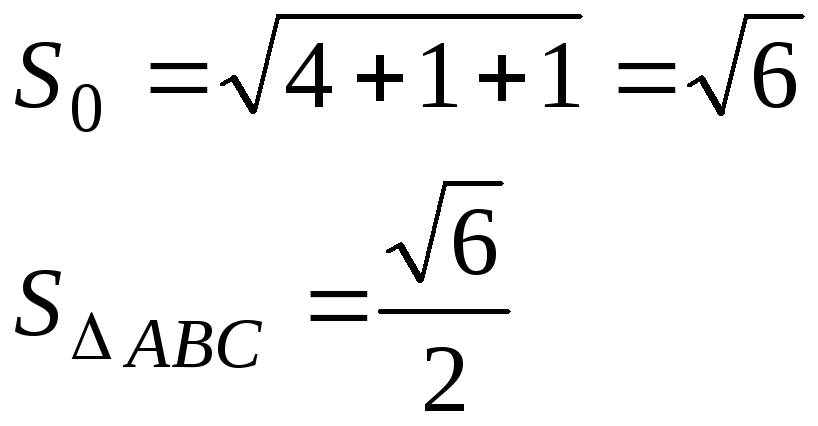
Пример № 2. Найти угол ВАС в треугольнике примера №1
 B
B
φ
A C

![]()
Смешанное произведение векторов.
Смешанным
произведением векторов
![]() ,
,
![]() ,
,
![]() называется скалярное произведение двух
векторов, один из которых сам является
векторным произведением.
называется скалярное произведение двух
векторов, один из которых сам является
векторным произведением.
Обозначают:
![]() .
.
Два основных свойства смешанного произведения:
1)
Свойство цикличности
![]() =
=
![]() .
.
Смешанное произведение не меняется при циклической перестановке составляющих его векторов.
2)
![]() =
=
![]()
![]() .
.
Если поменять местами любые два вектора в смешанном произведении, то его модуль не изменится, а знак поменяется на противоположный.
Геометрический смысл смешанного произведения.
Выясним геометрический смысл смешанного произведения. Для этого распишем подробно смешанное произведение, пользуясь определениями векторного и скалярного произведений.
![]() =
=![]()
=
![]() =
=
![]() параллелограмма
параллелограмма![]() S
параллелограмма ·h
S
параллелограмма ·h
V= S параллелограмма ·h
![]() – угол между
векторами
– угол между
векторами
![]() и
и
![]() ,
,
![]() –
угол между векторами
–
угол между векторами
![]() и
и
![]()

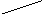





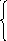
![]()
α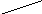





 h
h
![]()
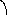
φ

![]()
Если построить на
этих трех векторах как на ребрах
параллелепипед, то получится выражение
численно равное объему. Смешанное
произведение
![]() численно равно объему параллелепипеда,
построенного на этих векторах как на
ребрах.
численно равно объему параллелепипеда,
построенного на этих векторах как на
ребрах.
Упорядоченная тройка векторов. Компланарные векторы. Условие компланарности.
Три ненулевых вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. В противном случае векторы называются некомпланарными. Так как все три компланарных вектора лежат в одной плоскости (а базис на плоскости состоит из двух векторов), то можно выразить один из компланарных векторов через два других вектора, если только они не колинеарны.
Пусть
в пространстве заданы три некомпланарных
вектора
![]() .
Эта тройка векторов называется
упорядоченной, если указано, какой из
них первый, второй, третий. Так как мы
работаем со свободными векторами, то
их можно поместить в одну и ту же любую
точку пространства.
.
Эта тройка векторов называется
упорядоченной, если указано, какой из
них первый, второй, третий. Так как мы
работаем со свободными векторами, то
их можно поместить в одну и ту же любую
точку пространства.
Упорядоченная тройка некомпланарных векторов называется правой, если первый, второй и третий векторы расположены относительно друг друга, как большой, указательный и средний пальцы правой руки. Если же они расположены как соответствующие пальцы левой руки, то такая упорядоченная тройка называется левой. Базис в пространстве, определение которого дано выше, дает пример правой тройки векторов. Если поменять направление любого базисного вектора на противоположное, то получим левую тройку векторов.
![]()



![]()
![]()
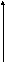
![]()


![]()
![]()
Смешанное
произведение
![]() (если
они некомпланарны) строго больше
0, если эти
векторы образуют правую тройку и строго
меньше 0, если они образуют левую тройку.
(если
они некомпланарны) строго больше
0, если эти
векторы образуют правую тройку и строго
меньше 0, если они образуют левую тройку.
Условие компланарности векторов.
Из чертежа видно,
что если
![]() находится в плоскости
находится в плоскости
![]() и
и
![]() ,
то объем параллелепипеда равен 0. Если
смешанное произведение трех ненулевых
векторов равно 0, то они компланарны.
,
то объем параллелепипеда равен 0. Если
смешанное произведение трех ненулевых
векторов равно 0, то они компланарны.
Вывод: три ненулевых вектора компланарны тогда и только тогда, когда их смешанное произведение равно 0. Это и есть условие компланарности трех векторов.
Запись смешанных произведений в координатах.
Пусть даны
![]()

Тогда условие
компланарности трех векторов
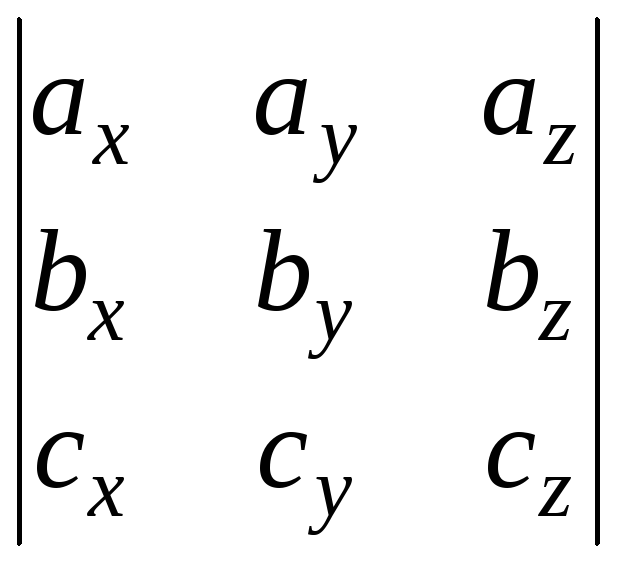 =0.
=0.
Пример: Даны четыре точки в пространстве. Найти объем тетраэдра ABCD.
A (1;1;1)
B (4;4;4)
C (3;5;5)
D (2;4;7) 

 D
D

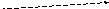
 A
C
A
C
B
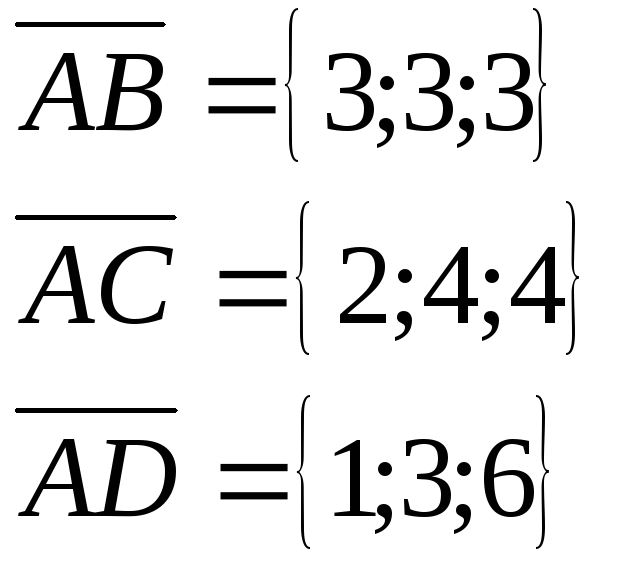
V тетраэдра
=
![]() V
параллелепипеда.
V
параллелепипеда.
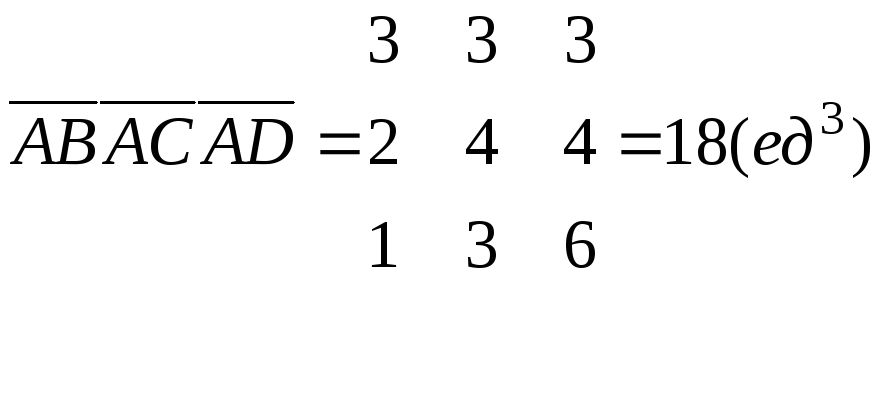
V
тетраэдра =
![]() ·
18 = 3(ед3).
·
18 = 3(ед3).
Аналитическая геометрия
Аналитическая геометрия на плоскости.
Угол наклона прямой и ее угловой коэффициент.
Рассмотрим на плоскости в прямоугольной декартовой системе координат некоторую произвольную прямую L.
 y
y
 L
L
С
В

x

А О
Так как количество углов между прямой L и осью ох бесконечно велико, то выберем из этого множества один угол, удовлетворяющий следующим условиям:
1) он отсчитывается от положительного направления оси ох против часовой стрелки.
2) он является наименьшим по модулю углом на который нужно повернуть ось ох вокруг точки А, чтобы совместить ее с прямой L.
Угол между прямой L и положительным направлением оси ох, удовлетворяющий этим двум условиям, называется углом наклона прямой L к оси ох.
Замечание: Угол можно отсчитывать от положительного направления оси ох и по часовой стрелке, но в этом случае угол считается отрицательным и берется со знаком минус.
Если прямая L параллельна оси ох, то ее угол наклона равен 0.
Тангенс угла наклона прямой называется ее угловым коэффициентом:
К = tg![]() .
.
Замечание: Если
прямая L
перпендикулярна оси ох
, то
![]() ,
и К не существует.
,
и К не существует.
Пусть даны точки
прямой В (х![]() ;у
;у![]() ),
С (х2;у2),
тогда из треугольника ВСD
получим:
),
С (х2;у2),
тогда из треугольника ВСD
получим:


 y2
C
y2
C
α

 y1
B
D
y1
B
D
 x1
x2
x1
x2
![]()
Вывод: Выразили угловой коэффициент прямой через координаты двух точек ее образующих.
Уравнение прямой с угловым коэффициентом.
Пусть задана прямая L в ПДСК на плоскости. Задача: вывести уравнение этой прямой, используя угловой коэффициент этой прямой и начальную ординату. Начальной ординатой прямой в ПДСК называется ордината точки пересечения этой прямой с осью оу:
 y
y
 L
L
N
M
 b
b

0 x
b-начальная ордината прямой L. Зададим координаты точек М и N: M (0;b),
N (x;y). Выразим угловой коэффициент прямой L через координаты этих точек:
уравнение
прямой с угловым коэффициентом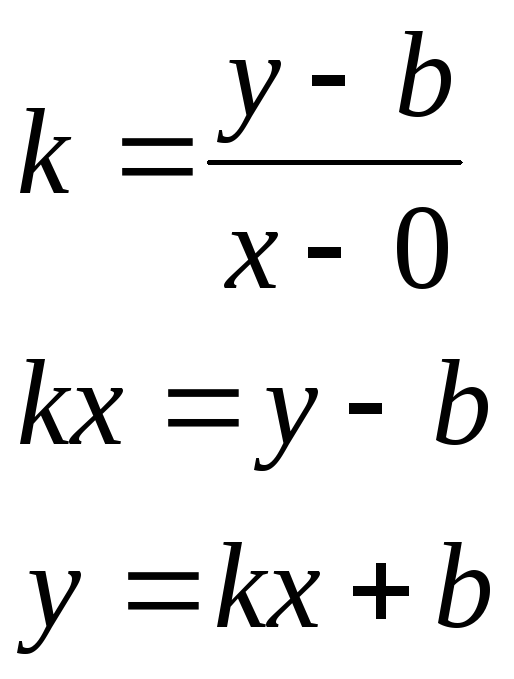
Замечание 1: Это уравнение отсутствует для прямых, перпендикулярных оси ох, потому что если угол наклона прямой равен 90°, то тангенс этого угла не существует. Любая прямая не перпендикулярная оси ох, называется наклонной прямой.
Замечание 2: Пусть b=0. Тогда Y=kx – уравнение прямой проходящей через начало координат.
Уравнение прямой, проходящей через данную точку и имеющей данный угловой коэффициент.
Пусть в ПДСК задана прямая L угловым коэффициентом k и точкой М, заданной своими координатами:
 y
y
L


 y0
M
y0
M
N

0 x0 x
k – угловой коэффициент прямой L,
М (х![]() ;
у
;
у![]() )–
заданная фиксированная точка прямой
L,
)–
заданная фиксированная точка прямой
L,
N (х; у) – произвольная (текущая) точка этой прямой.
авнение прямой
с угловым коэффициентом![]()
у
– у![]() =
k
(х – х
=
k
(х – х![]() )
– уравнение прямой, проходящей через
данную точку и имеющей данный угловой
коэффициент.
)
– уравнение прямой, проходящей через
данную точку и имеющей данный угловой
коэффициент.
Уравнение прямой, проходящей через две данные точки.
Пусть на плоскости в ПДСК дана прямая L, проходящая через две заданные точки М и N. Выведем уравнение этой прямой.
y
 P
• L
P
• L
N •
M
•

0 x
В
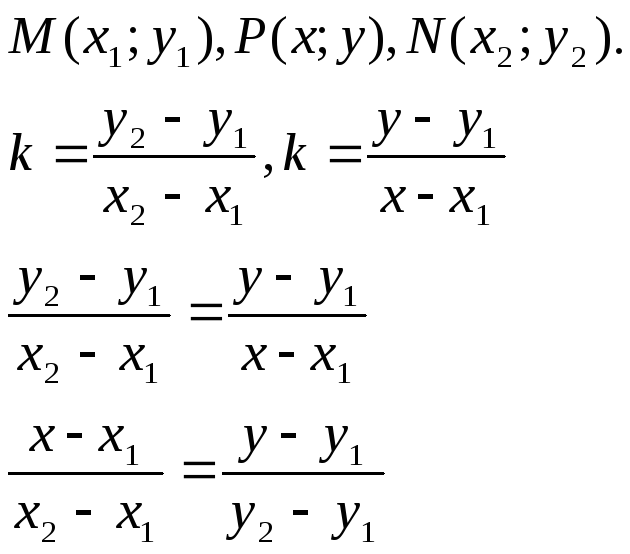
– уравнение
прямой, проходящей через две точки.
Угол между двумя прямыми. Условие параллельности и
перпендикулярности двух прямых на плоскости.
Пусть в ПДСК на
плоскости заданы две прямые L![]() и L
и L![]() ,
пересекающиеся в точке М под некоторым
углом. Задача: выразить тангенс этого
угла через угловые коэффициенты прямых.
,
пересекающиеся в точке М под некоторым
углом. Задача: выразить тангенс этого
угла через угловые коэффициенты прямых.
 y
y
0
 x
x
![]()
Разность углов наклона прямых L1 и L2 называется углом между двумя прямыми.
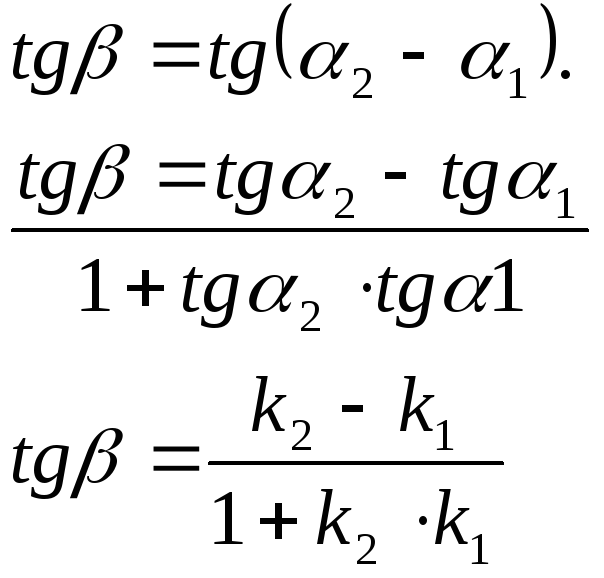
Рассмотрим два случая:
1)
Пусть L1//
L2,
тогда
![]() отсюда
отсюда
![]()
![]() то есть k
то есть k![]() = k
= k![]() .
.
Вывод:![]() если
прямые параллельны, то их угловые
коэффициенты равны.
если
прямые параллельны, то их угловые
коэффициенты равны.
2)
Пусть L1![]() L2,
тогда
L2,
тогда
![]() .
Так как tg
90° не существует, то знаменатель дроби
в формуле tg
.
Так как tg
90° не существует, то знаменатель дроби
в формуле tg![]() равен 0:
равен 0:
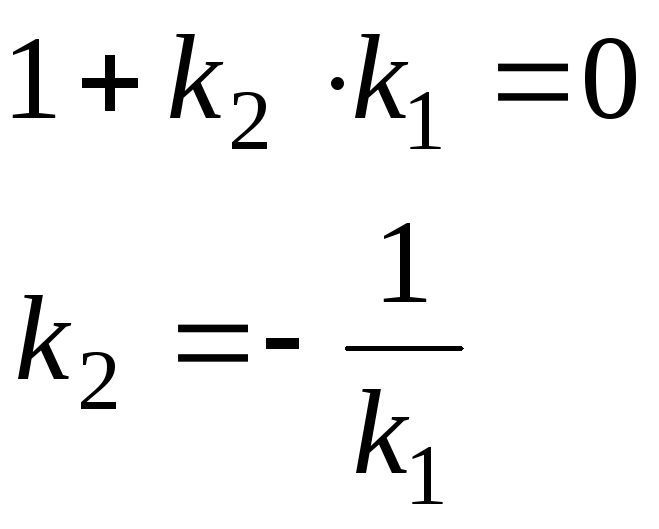
Последняя формула – условие перпендикулярности двух прямых на плоскости.
Прямая как линия первого порядка. Общее уравнение прямой.
Рассмотрим равенство Ах + Ву + С = 0, где А, В, С – некоторые заданные числа, а х и у – переменные величины, принимающие любые действительные значения. Это равенство можно понимать с алгебраической точки зрения как уравнение с двумя неизвестными х и у. Так как х и у входят сюда в первой степени, то это уравнение называется уравнением первого порядка с двумя неизвестными.
Докажем, что любая прямая на плоскости в ПДСК описывается таким уравнением Ах + Ву + С = 0, а любое такое уравнение задает в ПДСК прямую.
Теорема 1: Любая прямая в ПДСК на плоскости описывается уравнением
Ах + Ву + С = 0. Разобьем доказательство теоремы на два случая:
1)
![]() .
Тогда ее уравнение имеет вид х = а. Это
уравнение является частным случаем
уравнения Ах
+ Ву + С = 0,
когда В = 0, а
.
Тогда ее уравнение имеет вид х = а. Это
уравнение является частным случаем
уравнения Ах
+ Ву + С = 0,
когда В = 0, а
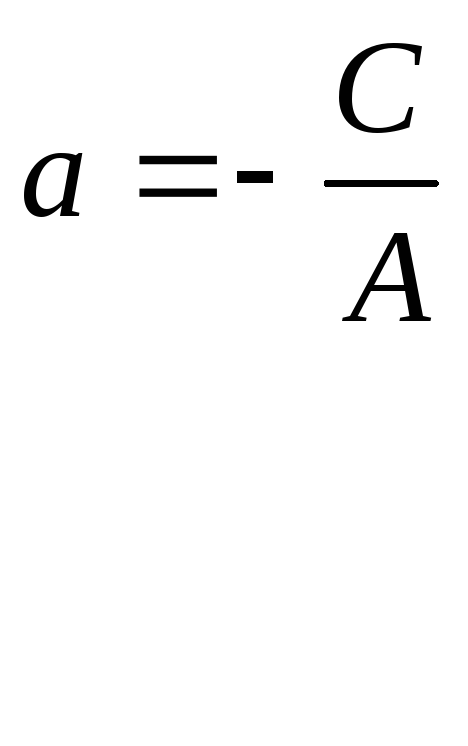

 у
L
у
L
 0
x
0
x
2) Прямая L – наклонная. Рассмотрим ее уравнение с угловым коэффициентом: y = kx + b. Это уравнение является частным случаем уравнения Ах + Ву + С = 0, когда В =1, k =А, b= – С.
Теорема 2: Любое уравнение вида Ах + Ву + С = 0 определяет в ПДСК на плоскости некоторую прямую.
Докажем
ее. Рассмотрим равенство Ах
+ Ву + С = 0. Так
как это одно уравнение с двумя
неизвестными, то оно имеет бесчисленное
множество решений. Пусть
![]() -
какое-то решение этого уравнения. Тогда
получим тождество
Ах
-
какое-то решение этого уравнения. Тогда
получим тождество
Ах![]() +
Ву
+
Ву![]() +
С
= 0. Вычтем из уравнения Ах
+ Ву + С = 0
почленно полученное тождество, тогда
придем к равенствам вида
+
С
= 0. Вычтем из уравнения Ах
+ Ву + С = 0
почленно полученное тождество, тогда
придем к равенствам вида

Обозначим:

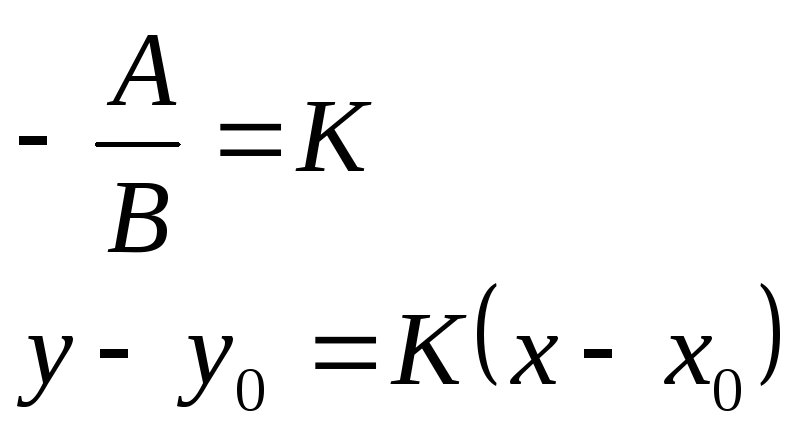 Получили
уравнение прямой, проходящей через
данную точку и имеющей данный угловой
коэффициент. Теорема доказана.
Получили
уравнение прямой, проходящей через
данную точку и имеющей данный угловой
коэффициент. Теорема доказана.
Обе доказанные теоремы позволяют утверждать, что любое равенство вида Ах + Ву + С = 0 является уравнением некоторой прямой в ПДСК на плоскости. Поэтому последнее равенство принято называть общим уравнением прямой на плоскости.
