-
Динамика популяций в биоценозах
Популяции в биоценозах обычно находятся в тесном взаимодействии. Одна популяция часто влияет на скорость роста или смертность другой. Так, члены одной популяции могут поедать членов другой популяции, конкурировать с ними за пищу, выделять вредные подавляющие развитие вещества или взаимодействовать с ними другим способом. Точно так же популяции могут быть полезными друг для друга, причем польза в одних случаях оказывается обоюдной, а в других – односторонней.
Для выяснения действий различных факторов в сложных природных ситуациях полезно пользоваться «моделями» в форме уравнений. Построение большинства моделей взаимодействия в биологических сообществах опирается на описание взаимодействия с помощью системы дифференциальных уравнений относительно численности видов xi(t). В предположении постоянства внешних и внутренних экологических факторов v1,v2,…,vm = const, а также без учета возрастной структуры популяций, динамику биоценоза, вызываемую межвидовыми взаимодействиями, можно описать с помощью системы дифференциальных уравнений вида
.
где функции fi(….) , стоящие в правых частях, представляют собой частные функции отклика абсолютных скоростей изменения плотности популяций на значения самих этих плотностей, равные разности абсолютных скоростей размножения и гибели при фиксированных значениях экологических факторов:
fi(x1,…,xn)
= Bi(
,…,
,
x1,…,xn)
– Di(
,…,
,
x1,…,xn).
То есть функции fi(…) описывают скорость изменения численности популяций в зависимости от структуры видовых взаимодействий.
Данная модель воспроизводит динамику видового состава биоценоза под влиянием одних биотических взаимодействий между популяциями, каждая из которых описывается на уровне полного внутрипопуляционного агрегирования, поскольку функции fi(…) зависят только от плотности популяций. Модели подобного типа называются биоценотическими моделями динамики популяций.
Предположим, что функции fi(…) не зависят явным образом от времени и рассматриваемая система дифференциальных уравнений является изолированной. Тогда из равенства xi = 0 вытекает fi(x1, x2,…, xi-1, 0, xi+1,…,xn) = 0 и fi(…) представимы в виде:
fi(x1, x2, …,xn) = xi ri(x1, x2, …,xn),
где ri(…) – удельная скорость изменения плотности популяции i-го вида (или обобщённый коэффициент прироста).
В простейшем случае в некоторой рассматриваемой области изменения плотностей популяций Xi= {xisxi(t)xie, i =1,.., n} удельные скорости изменения каждой популяции достаточно точно аппроксимируются линейными функциями плотностей
ri
(x1,
x2,
…,xn)
= rim
-
,
что приводит к системе уравнений
, (i=
1, 2,
…, n).
Модели такого типа в
литературе по экологии принято называть
вольтерровскими. Здесь
-
скорость естественного прироста в
отсутствии остальных видов, то есть
биотический потенциал i-го
вида;
- показатели внутривидового
взаимодействия, они отражают
характер взаимодействия видов. Матрицу
обычно
называют матрицей сообщества
или матрицей взаимодействия.
Коэффициенты
матрицы Г влияют на коэффициент
естественного прироста численности
i-го
вида при отсутствии других видов. Если
>0,
то говорят о наличии внутривидовой
конкуренции или самолимитирования
по численности i-го
вида. Как видно, для случая одного вида
данная система преобразуется к виду
логистического уравнения, описывающего
динамику популяций в среде с ограниченными
ресурсами.
Влияние j-го
вида на i-й
вид задано с помощью произведения
в соответствии с гипотезой «встреч и
эквивалентов». Число встреч особей
видов i и j
за время dt
равно
.
В результате этих встреч происходит
сокращение численности вида i
на величину
,
где
указывает на долю особей вида i,
которые истребляются при встрече
(0
1).
В тоже время число особей вида j
возрастает на величину
с некоторым коэффициентом пропорциональности,
называемым эквивалентом. Таким
образом, происходит немедленное
преобразование биомассы вида i
в биомассу вида j.
Представляет интерес
нахождение стационарного состояния
вольтерровской системы, то есть такой
комбинации численностей популяций
,
при которых производные
(скорости) обращаются в нуль. Положение
равновесия вольтерровской системы
должно удовлетворять системе уравнений
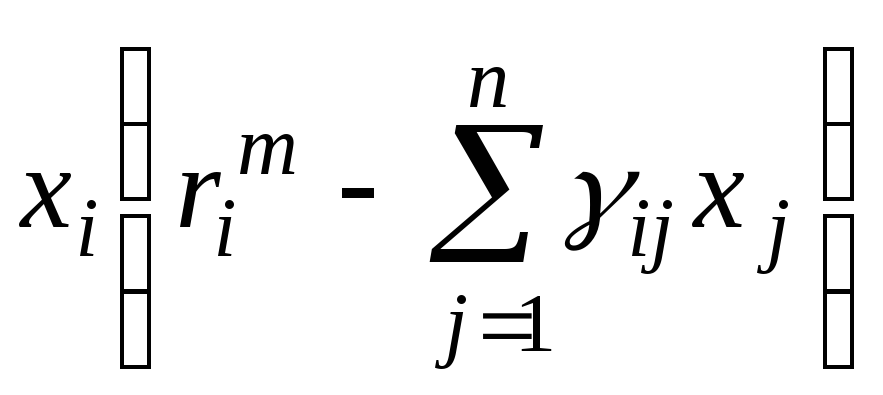=0
(i= 1, 2, …,
n).
Так как нас интересуют
только положительные и ненулевые
решения, то есть
,
то искомое положение равновесия является
решением системы уравнений
(i=
1, 2,
…, n).
или в матричной форме
ГХ = R ,
где R
=
,
Рассмотрим проблему устойчивости получаемого решения вольтерровской системы. При исследовании таких систем Вито Вольтерра рассматривал два подкласса таких систем – консервативные и диссипативные.
Для указанного рассмотрения проанализируем, как изменяется общая масса биоценоза
,
где
–
среднее значение биомассы особей вида
i. На траекториях
системы, задающей поведение скорости
изменения численностей популяций
,
общая биомасса сообщества будет
изменяться в соответствии с уравнением
.
Если квадратичная
форма
такова, что
,
то
вольтерровская система называется
консервативной. Если же
квадратичная форма
положительно определена, система
называется диссипативной.
Таким образом, для консервативных систем характерен неограниченный рост общей биомассы сообщества. В диссипативной системе рост общей биомассы замедляется вследcтвии влияния взаимодействия видов.
Для консервативной системы должно выполнятся:
, i,
j =
1,2,…,n
.
Таким образом,
коэффициенты
и
имеют противоположные знаки или
одновременно равны нулю.
Рассмотрим функцию Ляпунова вольтерровской системы
и вычислим
производную этой функции вдоль траектории
вольтерровской системы, представленной
в соответствии с
в следующем виде
.
Имеем
или
.
Если система
консервативна, то это выражение
тождественно равно нулю. Функция V(X)
является функцией Ляпунова для системы
=
и достигает минимального значения в
точке
.
Поскольку производная функции V(X)
тождественно равно нулю для всех
,
то положение равновесия X*
устойчиво.
Для консервативных систем в случае невырождённости матрицы Г и при чётном n первый интеграл имеет вид
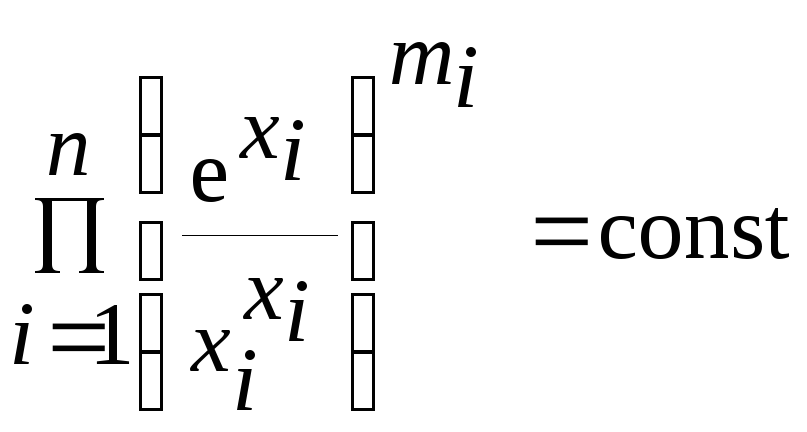
Отсюда следует, что при X* > 0 численности всех видов ограничены сверху и снизу положительными константами, и если X0 ≠ X*, то по крайней мере один вид имеет незатухающие колебания численности. Причём средние значения численности
Это свойство называется законом асимптотических средних.
В диссипативных системах квадратичная форма (X) положительно определена. Отсюда следует, что все ii > 0, то есть все виды должны обладать самолимитированием. Это говорит о том, что классы консервативных и диссипативных систем не пресекаются. Ещё одним необходимым условием диссипативности является неравенство нулю определителя матрицы Г, откуда сразу следует единственность решения системы ГХ=R. И, наконец, последнее необходимое условие состоит в том, что все главные миноры матрицы Г положительны.
Если Х* > 0, то для диссипативных систем первый интеграл системы имеет вид
,
где i = xi / xi*, c > 0. Поскольку квадратичная форма положительно определена, то, как показал В. Вольтерра, Х(t) Х* при t при любих начальных значениях Х0 = Х(0) Rn+ .
Кроме того, на траекториях диссипативной системы получаем dV/dt 0 для всех Х(t) Rn+ , причём равенство dV/dt = 0 выполняется только при Х(t) = Х*. Это означает, что Х(t) Х* при t , и положение равновесия асимптотически устойчиво при любых начальных данных из Rn+ , то есть областью асимптотической устойчивости является весь неотрицательный ортант.
Для решения вопроса о локальной устойчивости получаемого стационарного состояния Х*=Г-1R необходимо установить вид структурной матрицы системы Лотки-Вольтерра в точке Х*. Элемент (ij) этой матрицы определяют влияние j-го вида на динамику i-го вида
.
Поскольку функция fi(…) представима в виде
,
то при i j имеем
,
а при i = j имеем
.
Таким образом, матрица С(t) = Сij(t) (i = 1..n, j = 1...n) даёт исчерпывающую количественную характеристику всей совокупности биотических отношений между популяциями биоценоза в рассматриваемый момент времени t и поэтому называется структурной матрицей биоценоза.
Для системы Лотки-Вольтерра элементы структурной матрицы в стационарной точке Х* имеют вид
;
.
Теперь вопрос о локальной устойчивости точки Х* может быть решён путём применения одного из известных критериев, например, критерия Рауса-Гурвица.