
- •Популяция как компонент экосистемы
- •Популяция, ее структура и динамика
- •Понятие популяции в экологии
- •Плотность и численность популяций
- •Возрастной состав популяции
- •Пространственная структура популяции
- •Закономерности динамики популяций. Описание популяций на уровне полного внуприпопуляционного агрегирования
- •Биоценоз экосистемы
- •Динамика биоценоза как результат межвидовых взаимодействий
- •Видовое разнообразие стационарных биоценозов
- •Динамика популяций в биоценозах
- •Классификация биотических взаимодействий
- •Аменсализм (-, 0)
- •Конкуренция в широком смысле или интерференция (-, -)
- •Понятие экологической ниши и уравнения конкуренции
- •Управление численностью видов в экосистемах
-
Понятие экологической ниши и уравнения конкуренции
Пусть V
– пространство экофакторов.
Предположим, что ресурс, потребляемый
входящими в сообщество популяциями,
характеризуется вектором
![]() ,
а его объём
ограничен величиной
K(v).
Функцию K(v)
обычно называют спектром
ресурса. Потребление ресурса
видом і характеризуется
функцией предпочтения fi(v),
называемой часто функцией потребления.
Наиболее предпочитаемый ресурс vi,
соответствующий максимальному значению
функции fi,
принято называть центром ниши.
,
а его объём
ограничен величиной
K(v).
Функцию K(v)
обычно называют спектром
ресурса. Потребление ресурса
видом і характеризуется
функцией предпочтения fi(v),
называемой часто функцией потребления.
Наиболее предпочитаемый ресурс vi,
соответствующий максимальному значению
функции fi,
принято называть центром ниши.
Пусть xi(t)
– численность (биомасса) популяции i
в момент времени t.
Тогда произведение fi(v)xi(t)
описывает объём ресурса v,
потребляемого видом i.
Разность
![]() указывает на потенциальную возможность
сосуществования популяций, потребляющих
ресурс v. Если эта
разность достаточно велика, то можно
считать, что численность популяции
увеличивается в соответствии с законом
указывает на потенциальную возможность
сосуществования популяций, потребляющих
ресурс v. Если эта
разность достаточно велика, то можно
считать, что численность популяции
увеличивается в соответствии с законом
![]() (i=1,2,…,n).
(i=1,2,…,n).
Будем считать, что на рост популяции влияет относительная истощённость ресурса в точке v, равная
 .
.
При этом динамика численности популяции i будет описываться уравнением
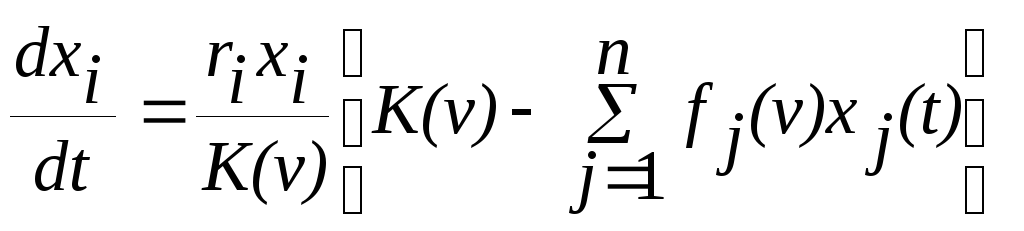 .
.
Обозначим
![]() .
Выражение Ki
имеет смысл общего объёма ресурсов,
потребляемых видом i
и называется ёмкостью ниши.
Умножив уравнение на
fi()
и проинтегрировав по всему пространству
ресурсов V, получим
.
Выражение Ki
имеет смысл общего объёма ресурсов,
потребляемых видом i
и называется ёмкостью ниши.
Умножив уравнение на
fi()
и проинтегрировав по всему пространству
ресурсов V, получим
![]() ,
,
где
![]() называются коэффициентами конкуренции.
Обозначив
называются коэффициентами конкуренции.
Обозначив
![]() ,
запишем уравнение конкуренции следующим
образом :
,
запишем уравнение конкуренции следующим
образом :
![]() .
.
Эта система является
диссипативной, поскольку при
![]() квадратичная форма
квадратичная форма

при всех x 0.
Т аким
образом, если существует положительное
решение системы уравнений
= R с коэффициентами
из выше рассмотренного уравнения
конкуренции, то оно является положением
равновесия, асимптотически устойчивым
в целом в положительном ортанте
аким
образом, если существует положительное
решение системы уравнений
= R с коэффициентами
из выше рассмотренного уравнения
конкуренции, то оно является положением
равновесия, асимптотически устойчивым
в целом в положительном ортанте
![]() .
.
Пусть функция потребления имеет гауссовский вид:
 ,
,
где
![]() – дисперсия нормального распределения.
– дисперсия нормального распределения.
Обозначим через dij расстояние между центрами vi и vj. Тогда коэффициенты конкуренции принимают вид

Если все
распределения имеют одинаковую дисперсию
![]() и
и
![]() ,
то
,
то
![]() ,
,
![]() .
.
Перепишем коэффициенты
конкуренции в виде
![]() ,
,
 .
Тогда получим матрицу конкуренции
.
Тогда получим матрицу конкуренции
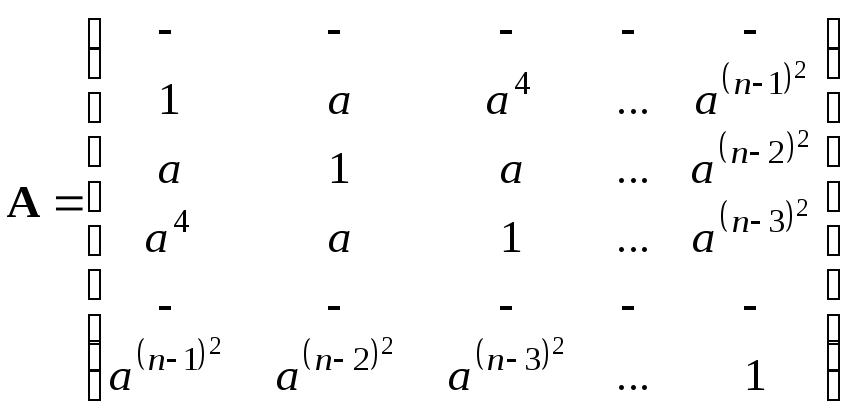
Величиной
![]() обычно характеризуют плотность видовой
упаковки сообщества или меру близости
экологических ниш. Диссипативность
матрицы
обычно характеризуют плотность видовой
упаковки сообщества или меру близости
экологических ниш. Диссипативность
матрицы
![]() сохраняется при всех даже достаточно
малых значениях
сохраняется при всех даже достаточно
малых значениях
![]() .
Поэтому положительное положение
равновесия будет асимптотически
устойчиво при видовой упаковке любой
плотности.
.
Поэтому положительное положение
равновесия будет асимптотически
устойчиво при видовой упаковке любой
плотности.
-
Отношения типа «жертва-эксплуататор» (+ , -)
К этой категории биотических отношений принадлежат любые отношения между двумя видами, при которых увеличение плотности популяции первого («жертвы») влечет за собой увеличение скорости роста популяции второго («эксплуататора»), тогда как увеличение плотности популяции второго вызывает уменьшение скорости роста популяции первого вида.
Наиболее важными примерами такого рода являются отношения:
-
растения и травоядного животного;
-
жертвы и хищника (в узком смысле этих терминов);
-
хозяина и паразита.
Из наблюдений над природными и антропогенными экосистемами известно, что при взаимодействиях типа «жертва-эксплуататор» возможны следующие основные «сценарии», изображающиеся характерными типами фазовых портретов на плоскости (x1, x2), где x1 – плотность популяции жертвы, а x2 – эксплуататора:
1. «Ускользание» жертвы от неэффективного эксплуататора.
В ид-эксплуататор
не способен прокормиться за счет данной
жертвы и со временем вымирает (
ид-эксплуататор
не способен прокормиться за счет данной
жертвы и со временем вымирает (![]() при
при
![]() ),
а сама жертва после некоторого переходного
процесса достигает определенной
стационарной численности
),
а сама жертва после некоторого переходного
процесса достигает определенной
стационарной численности
![]() .
Такое развитие событий нередко бывает
при попытках применения «биологического»
метода борьбы с вредителем путем введения
в рассматриваемую экосистему хищника
или паразита, уничтожающего вредный
вид.
.
Такое развитие событий нередко бывает
при попытках применения «биологического»
метода борьбы с вредителем путем введения
в рассматриваемую экосистему хищника
или паразита, уничтожающего вредный
вид.
2. Эксплуататор полностью истребляет жертву, после чего сам погибает от голода. Вид-эксплуататор слишком эффективен в поисках жертвы, прожорлив и быстро размножается, в результате чего он полностью истребляет жертву, после чего и сам погибает от голода. Например, травоядные на островах, лишенных хищников, выедают всю растительность и вымирают (см. рис. ниже).
3
 .
Существование «жестко» устойчивого
стационарного состояния. Из любого
начального состояния
.
Существование «жестко» устойчивого
стационарного состояния. Из любого
начального состояния
![]() система жестко (то есть без колебаний)
переходит в стационарную точку
система жестко (то есть без колебаний)
переходит в стационарную точку
![]() .
Этот вариант соответствует ситуации,
когда эксплуататор достаточно эффективен
и может быстро снижать численность
жертвы до низкого стационарного уровня
.
Этот вариант соответствует ситуации,
когда эксплуататор достаточно эффективен
и может быстро снижать численность
жертвы до низкого стационарного уровня
![]() ,
вблизи которого начинают действовать
некоторые механизмы, препятствующие
полному истреблению жертвы, как, например,
наличие укрытий, трудность обнаружения
редких экземпляров, наличие иммунной
прослойки и резкое ограничение числа
контактов в изреженной популяции жертвы.
,
вблизи которого начинают действовать
некоторые механизмы, препятствующие
полному истреблению жертвы, как, например,
наличие укрытий, трудность обнаружения
редких экземпляров, наличие иммунной
прослойки и резкое ограничение числа
контактов в изреженной популяции жертвы.
4. Наличие «мягко»
устойчивого стационарного состояния,
переход к которому осуществляется через
затухающие колебания. Из любого начального
состояния
![]() после переходного процесса с затухающими
колебаниями система стремится к своему
исходному состоянию
после переходного процесса с затухающими
колебаниями система стремится к своему
исходному состоянию
![]() ,
в котором жертва и эксплуататор могут
устойчиво существовать неограниченно
долго. Такой режим весьма характерен
для взаимодействия растений и копытных
растительноядных.
,
в котором жертва и эксплуататор могут
устойчиво существовать неограниченно
долго. Такой режим весьма характерен
для взаимодействия растений и копытных
растительноядных.
5 .
Существование устойчивого колебательного
режима типа «предельного цикла». Из
любого начального состояния
.
Существование устойчивого колебательного
режима типа «предельного цикла». Из
любого начального состояния
![]() траектория системы стремится к
единственной замкнутой траектории,
движение по которой осуществляется с
периодом T, то есть в системе возникают
автоколебания численностей
популяций. Наличие периодичных колебаний
численностей видов, необъяснимых
колебаниями внешних климатических
факторов, всегда ставила в тупик биологов.
И лишь исследования Лотки-Вольтерра
позволило объяснить эти колебания на
основе математического моделирования
системы «жертва-хищник».
траектория системы стремится к
единственной замкнутой траектории,
движение по которой осуществляется с
периодом T, то есть в системе возникают
автоколебания численностей
популяций. Наличие периодичных колебаний
численностей видов, необъяснимых
колебаниями внешних климатических
факторов, всегда ставила в тупик биологов.
И лишь исследования Лотки-Вольтерра
позволило объяснить эти колебания на
основе математического моделирования
системы «жертва-хищник».
В 1936 г. А. Н. Колмогоров предложил использовать
для описания динамики системы
«жертва-хищник» следующую систему
уравнений
1936 г. А. Н. Колмогоров предложил использовать
для описания динамики системы
«жертва-хищник» следующую систему
уравнений
 , (К.1)
, (К.1)
где
![]() и
и
![]() - удельные скорости роста жертвы и
эксплуататора. Методами качественной
теории дифференциальных уравнений
удалось доказать, что если функции
- удельные скорости роста жертвы и
эксплуататора. Методами качественной
теории дифференциальных уравнений
удалось доказать, что если функции
![]() и
и
![]() удовлетворяют ниже перечисленным
условиям.
удовлетворяют ниже перечисленным
условиям.
-
 – численность жертв возрастает, когда
оба вида малочисленны;
– численность жертв возрастает, когда
оба вида малочисленны; -
 – удельная скорость прироста популяции
жертвы является убывающей функцией
численности эксплуататора;
– удельная скорость прироста популяции
жертвы является убывающей функцией
численности эксплуататора; -
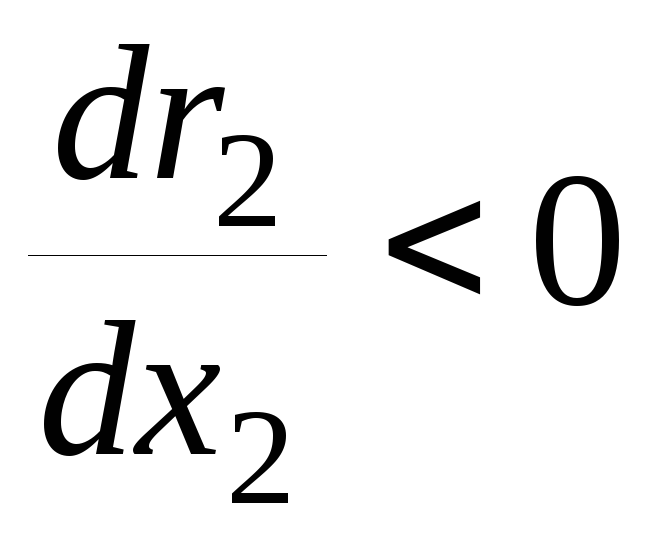 – размножение эксплуататоров замедляется
с ростом их численности;
– размножение эксплуататоров замедляется
с ростом их численности; -
 ,
,
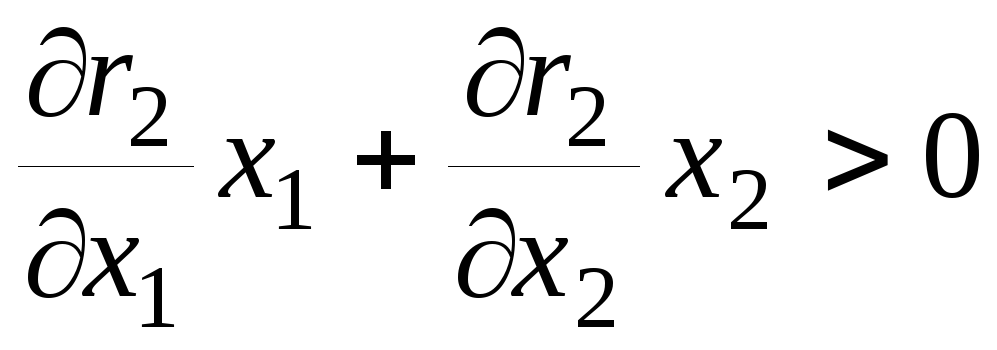 – при постоянном отношении численностей
жертв и эксплуататоров размножение
жертв замедляется с увеличением числа
эксплуататоров, а размножение
эксплуататоров стимулируется увеличением
числа жертв;
– при постоянном отношении численностей
жертв и эксплуататоров размножение
жертв замедляется с увеличением числа
эксплуататоров, а размножение
эксплуататоров стимулируется увеличением
числа жертв; -
 – существует критическая для эксплуататора
численность жертвы
– существует критическая для эксплуататора
численность жертвы
 ,
ниже которой он не может размножаться;
,
ниже которой он не может размножаться; -
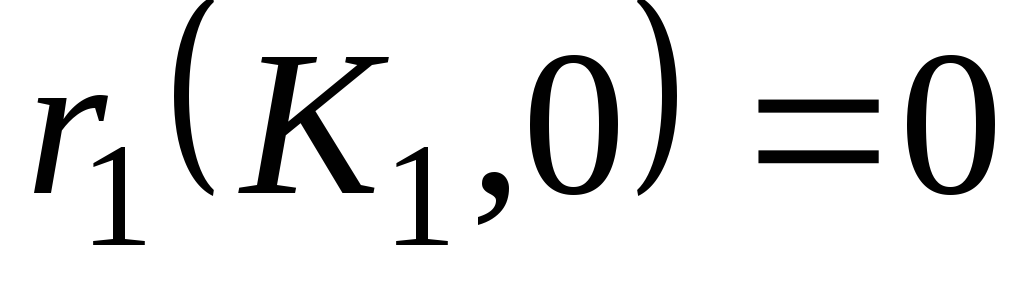 ,
,
 – существуют предельно высокие
численности жертвы
– существуют предельно высокие
численности жертвы
 и эксплуататора
и эксплуататора
 ,
после достижения которых рост жертвы
прекращается.
,
после достижения которых рост жертвы
прекращается.
В этом случае необходимым и достаточным
условием существования в модели (К.1)
устойчивого стационарного состояния
(сценарии 3 и 4) или устойчивого
колебательного режима (сценарий 5) будет
выполнение неравенства
этом случае необходимым и достаточным
условием существования в модели (К.1)
устойчивого стационарного состояния
(сценарии 3 и 4) или устойчивого
колебательного режима (сценарий 5) будет
выполнение неравенства
![]() .
.
При этом когда
![]() – емкость среды для жертвы, намного
превосходит плотность популяции жертвы
в стационарном состоянии
– емкость среды для жертвы, намного
превосходит плотность популяции жертвы
в стационарном состоянии
![]() ,
то можно ожидать наличия устойчивого
предельного цикла
,
то можно ожидать наличия устойчивого
предельного цикла
![]() .
Если же
.
Если же
![]() и
и
![]() различаются не очень сильно, то точка
различаются не очень сильно, то точка
![]() будет устойчивым стационарным состоянием.
В частности, достаточным условием
существования предельного цикла является
не отрицательность действительной
части характеристического уравнения
(
будет устойчивым стационарным состоянием.
В частности, достаточным условием
существования предельного цикла является
не отрицательность действительной
части характеристического уравнения
(![]() ):
):
 ,
,
где все частные производные вычислены в стационарной точке (х1*, х2*) .
Более содержательным является анализ менее общей модели, предложенной также Колмогоровым:
 ,
,
где r1(x1) = b1(x1) - d1(x1) – удельная скорость прироста жертвы в отсутствии эксплуататоров, r2(x1) = q(x1) - d2(x1) – удельная скорость прироста эксплуататора, (x1) – функция выедания (трофическая функция).
Колмогоров показал, что его вторая система имеет определенные решения, если функции r1(x1), r2(x1) и (x1) удовлетворяют условиям, приведенным ниже:
1)
![]() – внутривидовая конкуренция в
популяции жертвы усиливается с ростом
численности и препятствует ее чрезмерному
увеличению, при этом r1(x)
обращается в нуль при x1=
K1,
которое является верхней границей
численности популяции жертвы в отсутствии
хищников;
– внутривидовая конкуренция в
популяции жертвы усиливается с ростом
численности и препятствует ее чрезмерному
увеличению, при этом r1(x)
обращается в нуль при x1=
K1,
которое является верхней границей
численности популяции жертвы в отсутствии
хищников;
2)
![]() – в
отсутствие жертвы эксплуататор погибает,
а увеличение ее численности ускоряет
прирост численности эксплуататора;
– в
отсутствие жертвы эксплуататор погибает,
а увеличение ее численности ускоряет
прирост численности эксплуататора;
3) j(x1) > 0 при x1 > 0 – при наличии жертвы эксплуататор всегда способен ее обнаружить и только при x1 = 0 функция выедания обращается в нуль.
В этом случае вторая система Колмогорова может иметь только решения, описываемые сценариями (1), (3), (4) и (5) в зависимости от свойств функций r1(x1), r2(x1) и j(x1).
Стационарными точками системы являются (К1,0),где К1 определяется из уравнения r1(К1) = 0, и точка (x1*,x2*), которая является решением системы уравнений:
 или
или

Поведение решения второй системы Колмогорова существенным образом зависит от вида функции выедания j(х1), поэтому имеется большое число разнообразных моделей, отличающихся в первую очередь видом функции выедания. Рассмотрим простейшую модель функции выедания в виде линейной функции
j(х1) = g 12 х1,
где g12 = const > 0. Если принять рождаемость жертвы, смертность жертвы и эксплуататора – постоянной (b1 = const > 0, d1 = const > 0, d2 = const > 0), то получаем так называемую модель Лотки-Вольтерра системы “ хищник-жертва”:
 ,
,
где r1 = b1 - d1 , r2 = d2 и g21 = qg12.
Умножим первое уравнение на g21 и сложим со вторым, умноженным на g12:
![]() .
.
Далее умножим первое уравнение на r2/x1 и сложим со вторым, умноженным на r1/x2:
![]() .
.
Из двух полученных уравнений получаем
 .
.
Интегрируя, получаем
![]() ,
,
где
![]() .
.
Это уравнение описывает семейство замкнутых кривых с центром в точке:
x1* = r2/g21, x2* = r1/g12 .
Изучая поведение этих кривых, В.Вольтерра пришел к важному выводу о периодичности колебаний численности популяций и об устойчивости положения равновесия (х1*, х2*), которое является средним значением (х1, х2) по периоду колебаний Т. Действительно, перепишем рассматриваемую систему в виде
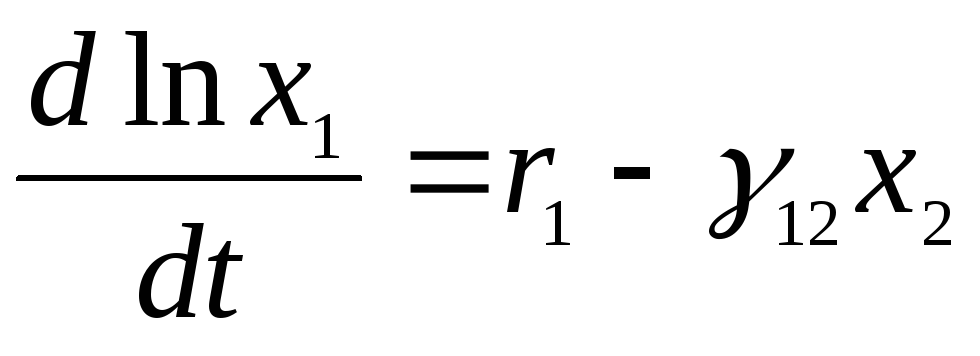 ,
,
 ,
,
и проинтегрируем обе части уравнений по интервалу времени, равному одному периоду колебаний, и с учетом периодичности получим
![]() ,
,
![]() .
.
1 2 3












![]()





![]()


![]()
![]()
Окончательно имеем
![]() ,
,
![]() .
.
Эти соотношения выражают закон сохранения средних значений: средние значения численностей хищников и жертв не зависят от начальных условий и равны численности в положении равновесия.
Если единовременно отстрелять часть животных, например, хищников, произойдет переход с траектории 1 на меньшую траекторию 2. При этом среднее число хищников не изменится, а лишь уменьшится колебаний численностей хищника и жертвы.
Если в системе хищник-жертва происходит искусственное уничтожение особей обоих видов, пропорционально их численности с коэффициентами пропорциональности a1 и a2, то система уравнений примет вид
![]()
![]()
Среднее значение численностей в этом случае составят
![]()
![]()
То есть, если 1 < r1 , то средняя численность популяций жертвы возрастает, а хищника – убывает. Это так называемый закон изменения средних. Если 1 > r1, то оба вида исчезают.
Если в модели Вольтерра учесть саморегулирование численности жертвы, то получим модифицированную систему Лотки-Вольтерра
![]() ,
,
![]()
Фазовый портрет этой системы соответствует сценарию 4 (переход в стационарное состояние через затухающие колебания), введение внутривидовой конкуренции среди жертв привело к стабилизации системы. Координаты стационарной точки равны:
x1* = r2/21 , x2* = r1/12 - 11r2/1221 .
