
- •«Физические основы электронной техники. Квантовая механика»
- •2. Движение микрочастицы в поле центральной
- •2.1. Поле центральной симметрии
- •2. 2. Атом водорода. Радиальная часть волновой функции
- •2.3. Схема уровней энергии и спектр атома водорода
- •2.4. Волновые функции атома водорода и распределение электронной плотности
- •2.5. Изотопический сдвиг и водородоподобные ионы
- •2.6. Энергетический спектр атомов щелочных металлов
Черняков Э.И. Лекции по дисциплине
«Физические основы электронной техники. Квантовая механика»
2. Движение микрочастицы в поле центральной
СИММЕТРИИ
2.1. Поле центральной симметрии
Поле
центральной симметрии характеризуется
тем, что потенциальная энергия
 частицы
в таком поле зависит только от расстояния
частицы
в таком поле зависит только от расстояния
 до некоторого центра. Задача заключается
в том, чтобы определить стационарные
состояния частицы, которая движется в
поле
до некоторого центра. Задача заключается
в том, чтобы определить стационарные
состояния частицы, которая движется в
поле
 .
.
Уравнение Шредингера для стационарных состояний в этом случае имеет вид
 .
(2.1)
.
(2.1)
Волновую
функцию
 удобнее искать как функцию сферических
координат
удобнее искать как функцию сферических
координат
 .
Мы должны найти однозначные, непрерывные
и конечные решения уравнения (2.1) во всей
области переменных (
.
Мы должны найти однозначные, непрерывные
и конечные решения уравнения (2.1) во всей
области переменных (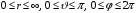 ).
Координаты
).
Координаты
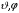 изменяются периодически. Воспользовавшись
(1.30) и (1.31), получим из (2.1)
изменяются периодически. Воспользовавшись
(1.30) и (1.31), получим из (2.1)
 .
(2.2)
.
(2.2)
Сферическая симметрия позволяет выделить в волновой функции радиальный и угловой множители
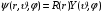 .
(2.3)
.
(2.3)
Подставим (2.3) в (2.2) и выполним некоторые преобразования
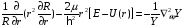 .
(2.4)
.
(2.4)
Левая
и правая часть (2.4) зависят от разных
независимых переменных, поэтому каждая
из них должна равняться одной и той же
постоянной, которую обозначим через
 .
.
Таким образом, для радиальной и сферической функций получаем следующие уравнения
 ,
(2.5)
,
(2.5)
 .
(2.6)
.
(2.6)
Уравнение
(2.5) зависит от вида потенциальной энергии
 .
Поэтому вид радиальных функций и
собственные значения энергии определяются
конкретным видом поля, в котором движется
частица. Уравнение (2.6) не зависит от
вида поля, в котором находится частица,
и решение этого уравнения для всех
сферически симметричных полей одинаково.
.
Поэтому вид радиальных функций и
собственные значения энергии определяются
конкретным видом поля, в котором движется
частица. Уравнение (2.6) не зависит от
вида поля, в котором находится частица,
и решение этого уравнения для всех
сферически симметричных полей одинаково.
Представив
 в виде
в виде
 (2.7)
(2.7)
и
обозначив постоянную разделение через
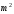 ,
для функций
,
для функций
 и
и
 получаем следующие уравнения:
получаем следующие уравнения:
 ,
(2.8)
,
(2.8)
 .
(2.9)
.
(2.9)
Условие нормировки (1.6) для волновой функции в этом случае можно предоставить в виде
 .
(2.10)
.
(2.10)
Решение (2.8) можно записать в виде
 ,
(2.11)
,
(2.11)
где
 –
постоянный множитель.
–
постоянный множитель.
Из
требования однозначности вытекает, что
 должно быть любым положительным или
отрицательным целым числом. Из условия
нормировки (2.10) получим
должно быть любым положительным или
отрицательным целым числом. Из условия
нормировки (2.10) получим
 .
Поэтому все собственные функции уравнения
(2.8) могут быть представлены в виде
.
Поэтому все собственные функции уравнения
(2.8) могут быть представлены в виде
 .
(2.12)
.
(2.12)
Перейдем
в уравнении (2.9) к новой переменной
 и
будем рассматривать
и
будем рассматривать
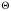 как
функцию
как
функцию
 .
Тогда имеем
.
Тогда имеем
 .
(2.13)
.
(2.13)
Функция
 должна
быть однозначной, непрерывной и конечной
при всех значениях угла
должна
быть однозначной, непрерывной и конечной
при всех значениях угла
 .
.
Уравнение
(2.13) называется присоединенным уравнением
Лежандра1.
В частном случае
 имеем уравнение Лежандра
имеем уравнение Лежандра
 ,
(2.14)
,
(2.14)
которое имеет решения при условии
 .
(2.15)
.
(2.15)
Решением
(2.14) (с точностью до множителя
 )
являются полиномы Лежандра
)
являются полиномы Лежандра

 (формула
Родрига), (2.16)
(формула
Родрига), (2.16)
а для (2.13) – присоединенные полиномы Лежандра
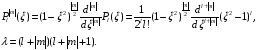 (2.17)
(2.17)
Из условия нормировки для присоединенных полиномов Лежандра
 (2.18)
(2.18)
и
условия нормировки для волновой функции
(2.10) определяем нормирующий множитель
в решении для функции
 .
Следовательно,
.
Следовательно,
 .
(2.19)
.
(2.19)
Окончательно
сферическую часть волновой функции
 можно
записать в виде
можно
записать в виде
 .
(2.20)
.
(2.20)
В
стационарном состоянии сохраняется
полная энергия, момент импульса (момент
количества движения) и проекция момента
импульса частицы. Другими словами
операторы
 ,
,
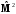 и
и
 должны
иметь общие собственные волновые
функции. Запишем уравнение для собственных
значений
должны
иметь общие собственные волновые
функции. Запишем уравнение для собственных
значений
 и
и
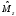
 ,
(2.21)
,
(2.21)
 ,
(2.22)
,
(2.22)
где операторы определяются (1.30) и (1.31). Воспользовавшись (2.7), (2.12) и (2.19), получим
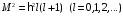 ,
(2.23)
,
(2.23)
 .
(2.24)
.
(2.24)
Эти
две формулы дают квантованные значения
величины момента импульса и его проекции
на ось
 .
Поскольку компонента
.
Поскольку компонента
 имеет
определенное значение, две другие
компоненты
имеет
определенное значение, две другие
компоненты
 и
и
 согласно (1.25) определенных значений не
могут иметь.
согласно (1.25) определенных значений не
могут иметь.
Определим
четность волновой функции
 .
Напомним, что выражение «волновая
функция имеет определенную четность»
означает, если в волновой функции
координаты
.
Напомним, что выражение «волновая
функция имеет определенную четность»
означает, если в волновой функции
координаты
 одновременно заменить на
одновременно заменить на
 ,
то абсолютная величина функции не
изменится, а ее знак либо не изменится
(четная функция), либо изменится на
противоположный (нечетная функция). В
сферической системе координат отражения
координат относительно начала координат
сводится к замене
,
то абсолютная величина функции не
изменится, а ее знак либо не изменится
(четная функция), либо изменится на
противоположный (нечетная функция). В
сферической системе координат отражения
координат относительно начала координат
сводится к замене
 на
на
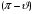 и
и
 на
на
 при неизменном значении
при неизменном значении
 .
Следовательно, четность
.
Следовательно, четность
 в (2.3) совпадает с четностью
в (2.3) совпадает с четностью
 .
.
Множитель
 имеет четность
имеет четность
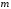 ,
поскольку
,
поскольку
 ,
а четность функции
,
а четность функции
 в соответствии с (2.12) определяется
четностью числа
в соответствии с (2.12) определяется
четностью числа
 .
Четность произведения этих сомножителей
совпадает с четностью числа
.
Четность произведения этих сомножителей
совпадает с четностью числа
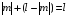 .
Следовательно, четность сферической
функции
.
Следовательно, четность сферической
функции
 определяется
четностью квантового числа
определяется
четностью квантового числа
 .
Четность полной волновой функции
частицы, которая движется в
центрально-симметричном поле, совпадает
с четностью квантового числа
.
Четность полной волновой функции
частицы, которая движется в
центрально-симметричном поле, совпадает
с четностью квантового числа
 .
.
Квантовое
число
 называют
орбитальным квантовым числом, а квантовое
число
называют
орбитальным квантовым числом, а квантовое
число
 –
магнитным.
–
магнитным.
Возможные
значения энергии
 определяются
из (2.5) и зависят от вида
определяются
из (2.5) и зависят от вида
 .
Кроме того, они могут зависеть от
.
Кроме того, они могут зависеть от
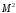 (через число
(через число
 ),
но не зависят от
),
но не зависят от
 (и числа
(и числа
 ).
Это можно объяснить тем, что мы имеем
дело с центрально-симметричным полем,
а поэтому все направления в пространстве
физически равноправны, и энергия не
может зависеть от ориентации в пространстве
момента импульса.
).
Это можно объяснить тем, что мы имеем
дело с центрально-симметричным полем,
а поэтому все направления в пространстве
физически равноправны, и энергия не
может зависеть от ориентации в пространстве
момента импульса.
В
реальных физических системах взаимодействие
на больших расстояниях бесконечно мало.
Это означает, что потенциальная энергия
 ,
и мы можем считать
,
и мы можем считать
 .
.
Характер
решения уравнения (2.5) зависит от того,
больше или меньше полная энергия
 значения потенциальной энергии, то есть
значения потенциальной энергии, то есть
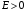 или
или
 .
Воспользуемся подстановкой
.
Воспользуемся подстановкой
 .
(2.25)
.
(2.25)
В этом случае уравнение (2.5) принимает вид
 .
(2.26)
.
(2.26)
Сначала
рассмотрим асимптотическое решение
этого уравнения при
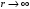 .
Пренебрегая для больших
.
Пренебрегая для больших
 членом с
членом с
 и
и
 (при нашем условии
(при нашем условии
 ),
получим простое уравнение
),
получим простое уравнение
 .
(2.27)
.
(2.27)
Обозначив
 и
и
 ,
(2.28)
,
(2.28)
получим общее решение в виде
 ,
(2.29)
,
(2.29)
 ,
(2.30)
,
(2.30)
где
 и
и
 –
произвольные постоянные. Согласно с
(2.25) асимптотическое решение уравнения
(2.5) имеет вид
–
произвольные постоянные. Согласно с
(2.25) асимптотическое решение уравнения
(2.5) имеет вид
 ,
(2.31)
,
(2.31)
 .
(2.32)
.
(2.32)
В
первом случае ( )
решение представляет собой суперпозицию
расходящихся и сходящихся сферических
волн. Вероятность найти частицу в этом
случае не исчезает даже при больших
)
решение представляет собой суперпозицию
расходящихся и сходящихся сферических
волн. Вероятность найти частицу в этом
случае не исчезает даже при больших
 .
Вероятность найти ее между
.
Вероятность найти ее между
 и
и
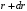 пропорциональна
пропорциональна
 и объему слоя
и объему слоя
 :
:
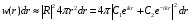 .
(2.33)
.
(2.33)
Такие
состояния отвечают апериодическим
орбитам в
классической механике, когда частица
движется из бесконечности к центру сил
и опять уходит на бесконечность. Поскольку
состояние стационарно, поток частиц,
которые приходят, должен равняться
потоку частиц, которые уходят. Это
означает, что
 .
При этом условии решение (2.31) можно
представить в виде стоячей сферической
волны
.
При этом условии решение (2.31) можно
представить в виде стоячей сферической
волны
 ,
(2.34)
,
(2.34)
где
 и
и
 –
действительные постоянные.
–
действительные постоянные.
Рассмотрим
случай
 .
В (2.32) необходимо положить
.
В (2.32) необходимо положить
 ,
иначе
,
иначе
 при
при
 .
Тогда
.
Тогда
 ,
(2.35)
,
(2.35)
и для этих состояний
 .
(2.36)
.
(2.36)
Это
означает, что
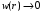 при
при
 ,
то есть частицу можно найти только возле
центра сил. Такие состояния отвечают
периодическим
орбитам в
классической механике, когда частица
движется вокруг силового центра.
,
то есть частицу можно найти только возле
центра сил. Такие состояния отвечают
периодическим
орбитам в
классической механике, когда частица
движется вокруг силового центра.
Можно
доказать, что решение (2.31) уравнения
(2.26) имеет место при любых значениях
энергии
 ,
то есть при
,
то есть при
 мы имеем непрерывный
спектр энергии.
При
мы имеем непрерывный
спектр энергии.
При
 будем иметь дискретный
спектр энергии.
Это мы покажем на примере кулоновского
поля.
будем иметь дискретный
спектр энергии.
Это мы покажем на примере кулоновского
поля.
