2. 2. Атом водорода. Радиальная часть волновой функции

Наиболее простой задачей квантовой механики является задача о движении электрона в кулоновском поле ядра. В атоме водорода, ионах и других многозарядных ионах, которые имеют лишь один электрон, потенциальная энергия электрона в поле ядра имеет вид ²

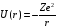, (2.37)(2.2.1)

где – заряд ядра.

Подставим (2.37) в (2.26) и получим

. (2.38)

Под понимается приведенная масса электрона

, (2.39)

где – масса ядра, – масса покоя электрона.

Введем атомные единицы длины и энергии

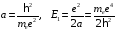(2.40)

и перейдем к безразмерным величинам

и . (2.41)

Это позволяет представить уравнение (2.38) в удобном для решения виде

. (2.42)

Рассмотрим сначала асимптотические решения (2.42).

При 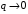(вблизи ядра) уравнение принимает вид

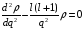. (2.43)

Решение ищем в форме 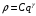. Подставив 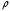в (2.43), получим квадратное уравнение , которое имеет два корня 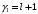и 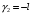. Второй корень нас не удовлетворяет, поскольку решение будет расходящимся. Таким образом, имеем

. (2.44)

При (на большом расстоянии от ядра) уравнение (2.42) приобретает вид

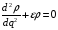. (2.45)

Здесь возможные два случая: 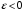и . Второй случай приводит к апериодическим орбитам в классической механике (см. раздел 2.1) и нас не интересует. Первый описывает связанные состояния.

Обозначив 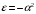, получим решение (2.45) в следующем виде

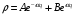. (2.46)

Поскольку решение должно быть конечным, положим и получим

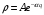. (2.47)

Воспользовавшись асимптотическими решениями (2.44) и (2.47), запишем решение, которое будет справедливым для любой области

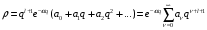. (2.48)

Подставляя ряд (2.48) в (2.42) и перегруппируя члены, получим

(2.49)

Приравнивая коэффициенты при одинаковой степени 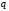нулю, находим рекуррентные соотношение для неизвестных коэффициентов :

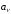. (2.50)

При 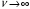коэффициенты ведут себя 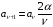и сумма ряда . Следовательно, решение для расходящееся. Поэтому необходимо ограничить ряд (2.49). Для этого будем считать, что начиная с некоторого 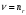коэффициент , в то время как . При этом условии из (2.50) получим

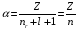, (2.51)

где 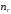называется радиальным квантовым числом, а – главным квантовым числом, и они могут принимать следующие значения

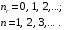(2.52)

Воспользовавшись (2.51) и (2.50), найдем коэффициенты многочлена (2.48) через коэффициент , а затем и сам многочлен:

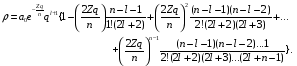(2.53)

Целесообразно ввести новую переменную:

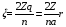. (2.54)

Объединяя все постоянные множители в один , мы получим из (2.25) и (2.53) функцию, которая принадлежит квантовым числам и :

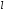, (2.55)

где через обозначен многочлен, который заключен в фигурные скобки в формуле (2.53). Этот многочлен вычисляется с помощью производной от многочлена Лагерра³ 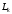, который определяются по формуле

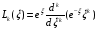. (2.56)

Тогда под многочленом 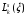понимают многочлен

. (2.57)

Нетрудно убедиться, что когда и , мы получим многочлен, который содержится в фигурных скобках выражения (2.53).

Формулы (2.56) и (2.57) позволяют легко вычислять функции . Множитель в (2.55) определяется из условия нормировки (2.10) и равняется

. (2.58)

Иногда полезно знать средние значения некоторых степеней в стационарных состояниях. Например,

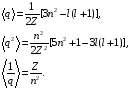(2.59)