
- •3)Доверительный интервал для математического ожидания
- •6)Проверка гипотезы о равенстве дисперсий
- •7)Проверка гипотезы о равенстве средних (независимые выборки)
- •8)Проверка гипотезы о равенстве средних значений
- •9)Проверка гипотезы о равенстве средних двух нормальных совокупностей
- •10)Таблицы наблюдений
- •11)Метод наименьших квадратов
- •12)Элементы регрессионного анализа
- •13)Доверительный интервал для линейной регрессии
- •14)Критерий хи-квадрат
- •15)Критерий независимости признаков
- •16)Критерий Вилкоксона проверки однородности выборок
- •17)Закон Мальтуса.
- •19)Обобщенная логистическая популяция
- •20)Фазовый портрет автономной линейной системы второго порядка
- •21)Система «хищник – жертва».
- •23)Процесс выживаемости популяций
- •24)Ориентированные графы
- •25)Примеры орграфов.
- •26)Динамика развития орграфа
1)Результаты наблюдений, записанные в порядке возрастания вариант:
![]()
![]()
называются вариационным рядом.
Последовательность
чисел
![]() называется
статистическим
рядом и
записывается в виде таблицы.
называется
статистическим
рядом и
записывается в виде таблицы.
|
|
|
|
. . . |
|
|
|
|
|
. . . |
|
Для непрерывных признаков и при большом объеме выборки данные группируются, и результаты представляются в виде интервального статистического ряда.
2)Статистической
оценкой математического ожидания
![]() называется среднее арифметическое
элементов выборки, которая называется
выборочное
среднее и
обозначается
называется среднее арифметическое
элементов выборки, которая называется
выборочное
среднее и
обозначается
![]() .
.
Для выборки объемом
n,
заданной вариационным рядом
![]() :
:
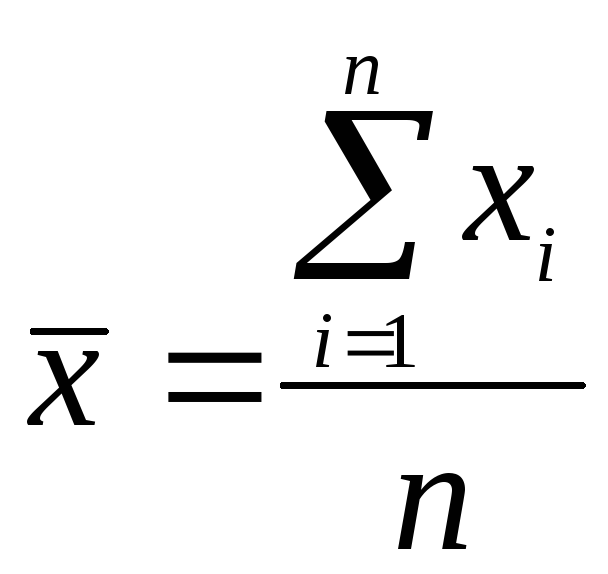 .
.
Для определения рассеяния значений признака около математического ожидания рассматривается параметр, который называется дисперсией распределенияD(X) (генеральной дисперсией) и который определяетсяпо формуле:
![]()
Оценки дисперсии и
среднеквадратичного отклонения
Для выборки
![]() статистическая оценка дисперсии,
удовлетворяющая требованиям состоятельности
и несмещенности, имеет вид
статистическая оценка дисперсии,
удовлетворяющая требованиям состоятельности
и несмещенности, имеет вид
 , (4)
, (4)
Среднеквадратическое
отклонение (стандартное отклонение)
![]() оценивается величиной
оценивается величиной
![]() , (5)
, (5)
которая называется выборочным стандартным отклонением. Тем самым
![]() и
и ![]() .
.
3)Доверительный интервал для математического ожидания
Случай известной дисперсией
Условие (1) для математического ожидания принимает вид
![]() (2)
(2)
Для нормального распределения
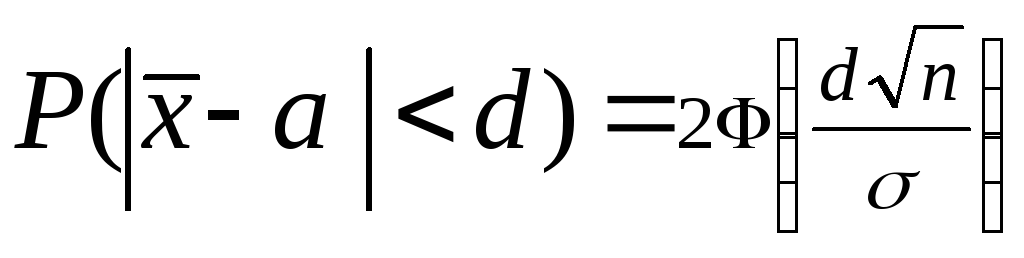 . (3)
. (3)
Из (2) и (3) имеем уравнение для определения d
![]() . (4)
. (4)
Введем обозначение:
![]() .
.
Тогда
![]() .
.
Значение
![]() определяется по таблице 2 значений
функции Лапласа.
определяется по таблице 2 значений
функции Лапласа.
Например, для![]()
![]() и в таблице 2 находим:
и в таблице 2 находим:
|
|
|
|
1,96 |
0,4750 |
Следовательно,![]() .
.
После определения
![]() определяем точность оценки по формуле:
определяем точность оценки по формуле:
![]() (5)
(5)
и границы доверительного интервала:
![]() и
и
![]() (6)
(6)
Таким образом, с
надежностью
![]() доверительный интервал
доверительный интервал
![]() содержит в себе генеральное среднее
(математическое ожидание) а.
содержит в себе генеральное среднее
(математическое ожидание) а.
Оценка достоверности различий между результатами измерений и фиксированной величиной с помощью доверительного интервала
В практической деятельности по контролю состояния окружающей среды нередко возникает необходимость сравнить результаты измерений с какой-либо заданной фиксированной величиной. Наиболее типичный случай – сравнение с величиной предельно допустимой концентрации (ПДК) загрязняющего вещества в объектах окружающей среды.
Пусть фиксированная величина – ПДК, тогда
если
![]() >
ПДК
>
ПДК
![]() ПДКпревышена
(с надежностью
ПДКпревышена
(с надежностью
![]() ):
):
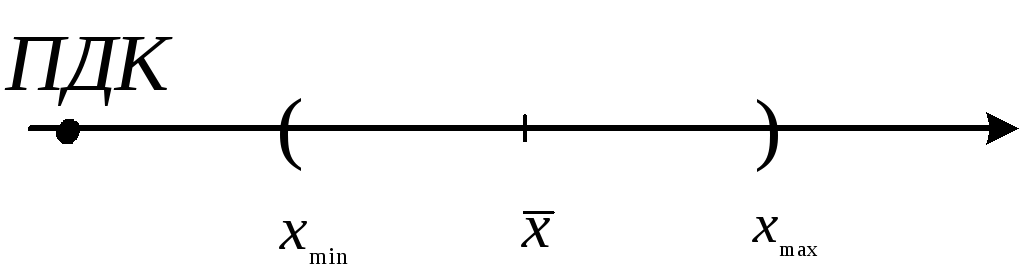
если
![]() <
ПДК
<
ПДК
![]() ПДК
не превышена (с надежностью
ПДК
не превышена (с надежностью
![]() ):
):
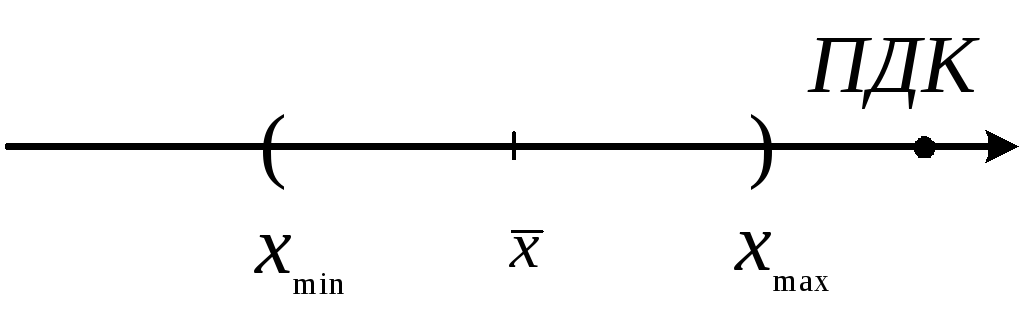
если
![]() <ПДК
<
<ПДК
<![]()
![]() различия между
различия между![]() и ПДК недостоверны (с надежностью
и ПДК недостоверны (с надежностью
![]() ):
):
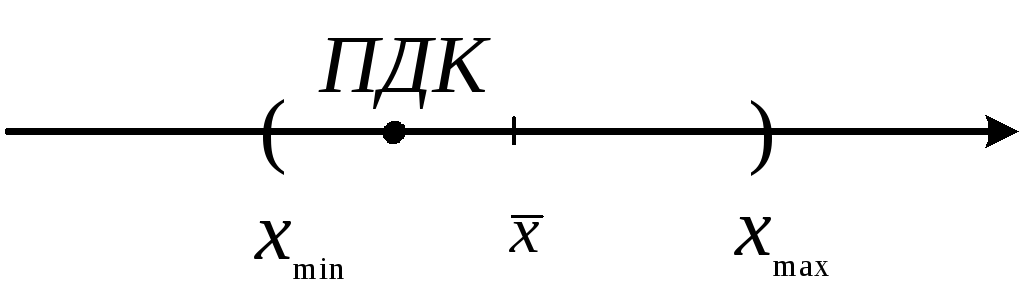 .
.
В![]() %
случаев наши выводы могут оказаться
неверными.
%
случаев наши выводы могут оказаться
неверными.
4)Случай больших выборок.
Приведенные выше
расчеты доверительного интервала
применяются
и в случаях с неизвестной дисперсии,
но только если
объем выборок
![]() ,
т.е. в случаях больших выборок.
,
т.е. в случаях больших выборок.
В этом случае в
формулах (3) и (4) вместо![]() используется его вычисленная по выборке
несмещенная оценка
используется его вычисленная по выборке
несмещенная оценка
![]() ,
т.е. считаем, что
,
т.е. считаем, что
![]() .
.
Минимальный объем выборки.
Если требуется
оценить математическое ожидание с
наперед заданной точностью оценки d
и надежностью
![]() ,
то из формулы (3) получим формулу для
минимального объема выборки, который
обеспечит эту точность:
,
то из формулы (3) получим формулу для
минимального объема выборки, который
обеспечит эту точность:
![]() .
.
5)Статистической гипотезой называется предположение о виде распределения или о параметрах известных распределений.
Ошибки принятия гипотез
Ошибка 1 рода состоит в том, что будет отвергнута правильная гипотеза.
Ошибка 2 рода состоит в том, что будет принята неправильная гипотеза.
|
|
принимается |
отвергается |
|
верна |
Решение правильное |
Ошибка 1 рода |
|
неверна |
Ошибка 2 рода |
Решение правильное |
Вероятность
![]() допустить ошибку 1 рода называют уровнем
значимости.
допустить ошибку 1 рода называют уровнем
значимости.
Вероятность
![]() задается заранее, при этом обычные
значения
задается заранее, при этом обычные
значения
![]() : 0,1; 0,05; 0,005; 0,001.
: 0,1; 0,05; 0,005; 0,001.
6)Проверка гипотезы о равенстве дисперсий
На практике задача сравнения дисперсий возникает, если требуется сравнить точность приборов, инструментов, методов измерений, технологий.
Очевидно, предпочтительнее взять тот прибор, инструмент и т.п., который обеспечивает наименьшее рассеяние результатов измерений, т.е. наименьшую дисперсию.
Проведем измерения на двух приборах.
Пусть все возможные
измерения первым прибором − Х
и этим прибором проведено
![]() измерений, и по ним вычислена
измерений, и по ним вычислена
![]() − оценка
− оценка
![]() .
.
Пусть все возможные
измерения вторым прибором − Y
и этим прибором проведено
![]() измерений, и по ним вычислена
измерений, и по ним вычислена
![]() − оценка
− оценка
![]() ,
причем
,
причем
![]() .
.
Требуется по
выборочным средним и заданном![]() проверить значимость этого различия.
проверить значимость этого различия.
Краткое условие:
Х: ![]()
![]() ,
,
Y: ![]()
![]() , причем
, причем ![]() .
.
Сформулируем гипотезу:
![]()
![]()
Зададим
![]() или
или
![]() в зависимости от конкретной задачи.
в зависимости от конкретной задачи.
Вычислим
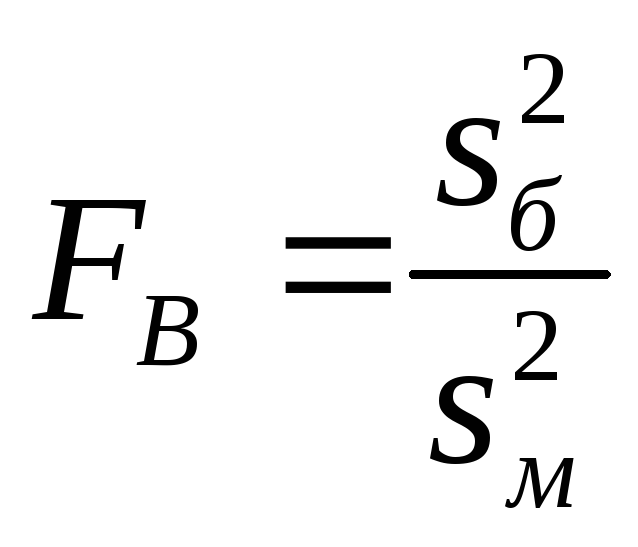 ,
,
где
![]() - большая дисперсия, а
- большая дисперсия, а
![]() - меньшая дисперсия.
- меньшая дисперсия.
Соответствующая случайная величина F − статистический критерий данной задачи − имеет распределение Фишера – Снедекора.
Если
![]() ,
то выборочное значение критерия
,
то выборочное значение критерия
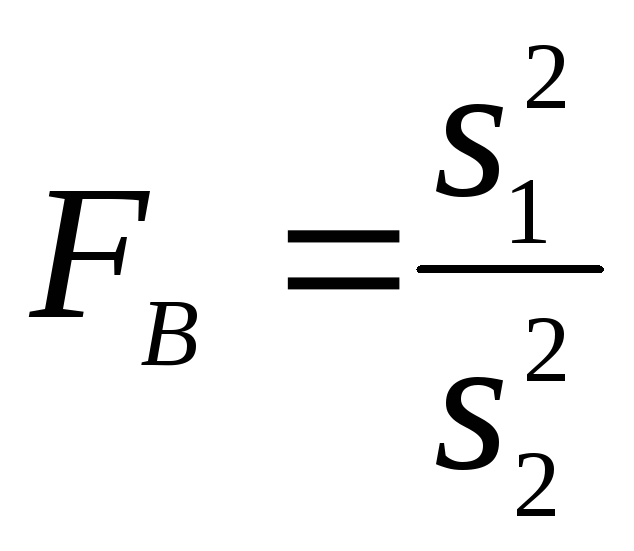 .
.
Критическая область - правосторонняя.
Для определения
![]() найдем степени
свободы:
найдем степени
свободы:
![]() ,
,
![]()
где
![]() - объем выборки с большей дисперсией
- объем выборки с большей дисперсией
![]()
![]() - объем выборки с
меньшей дисперсией
- объем выборки с
меньшей дисперсией
![]() .
.
Критические
значения распределения Фишера представлены
в таблице 7
![]() или
или
![]() .
.
