
- •3)Доверительный интервал для математического ожидания
- •6)Проверка гипотезы о равенстве дисперсий
- •7)Проверка гипотезы о равенстве средних (независимые выборки)
- •8)Проверка гипотезы о равенстве средних значений
- •9)Проверка гипотезы о равенстве средних двух нормальных совокупностей
- •10)Таблицы наблюдений
- •11)Метод наименьших квадратов
- •12)Элементы регрессионного анализа
- •13)Доверительный интервал для линейной регрессии
- •14)Критерий хи-квадрат
- •15)Критерий независимости признаков
- •16)Критерий Вилкоксона проверки однородности выборок
- •17)Закон Мальтуса.
- •19)Обобщенная логистическая популяция
- •20)Фазовый портрет автономной линейной системы второго порядка
- •21)Система «хищник – жертва».
- •23)Процесс выживаемости популяций
- •24)Ориентированные графы
- •25)Примеры орграфов.
- •26)Динамика развития орграфа
16)Критерий Вилкоксона проверки однородности выборок
Критерий
![]() обычно применяется в случае больших
объемов
выборок. При небольших объемах применяется
критерий Вилкоксона.
обычно применяется в случае больших
объемов
выборок. При небольших объемах применяется
критерий Вилкоксона.
Критерий применяется к случайным величинам, распределения которых неизвестны. Не требуется нормальности распределения выборок.
Требуется, чтобы признаки были непрерывными величинами.
Имеем две выборки
![]()
![]()
Если две выборки однородны, то они извлекаются из одной генеральной совокупности и имеют одинаковые неизвестные непрерывные функции распределения:
![]() и
и ![]() .
.
Для обеих выборок значения аргумента функций распределения будем обозначать через x.
![]()
![]()
(двусторонняя критическая область)
![]()

![]()
![]() в том смысле, что
мы большие значения встретим скорее у
распределения X,
чем у Y.
в том смысле, что
мы большие значения встретим скорее у
распределения X,
чем у Y.
(критическая область − правосторонняя)
![]()
(критическая область − левосторонняя)
Расположим выборки так, что
![]() (1)
(1)
Случай 1.
![]() (2)
(2)
Правило проверки гипотез.
-
Расположить варианты обеих выборок в возрастающем порядке, т.е. в виде одного общего вариационного ряда, и найти в этом ряду
 - сумму порядковых номеров вариант
первой
выборки.
- сумму порядковых номеров вариант
первой
выборки.
Порядковые номера называются ранги.
-
По таблице 11 найти нижнюю критическую точку
![]() ,
,
где
в случае
![]() :
:
![]()
в случае
![]() и
и
в случае
![]() :
:
![]()
-
Найти верхнюю критическую точку
![]() . (3)
. (3)
-
Проверить принадлежность
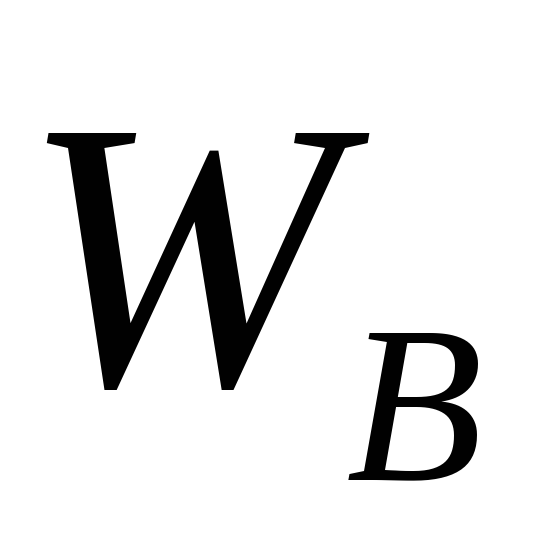 критической области:
критической области:
в случае
![]()

если
![]() принимаем (наблюдения двух выборок
принадлежат одной генеральной
совокупности);
принимаем (наблюдения двух выборок
принадлежат одной генеральной
совокупности);
если
![]() принимаем (наблюдения принадлежат
разным совокупностям).
принимаем (наблюдения принадлежат
разным совокупностям).
в случае
![]()

если
![]() принимаем;
принимаем;
если
![]() принимаем (наблюдения принадлежат
разным совокупностям, причем большие
значения встретим скорее у распределения
X,
чем у Y).
принимаем (наблюдения принадлежат
разным совокупностям, причем большие
значения встретим скорее у распределения
X,
чем у Y).
в случае
![]()

если
![]() принимаем;
принимаем;
если
![]() принимаем (наблюдения принадлежат
разным совокупностям, причем большие
значения встретим скорее у распределения
Y,
чем уX).
принимаем (наблюдения принадлежат
разным совокупностям, причем большие
значения встретим скорее у распределения
Y,
чем уX).
Замечание. В случае с) можно не вычислять верхнюю критическую точку.
Случай 2.
![]()
в случае
![]() :
:
![]()
 (4)
(4)
где знак
![]()
![]() означает, целую часть числа а,
а
означает, целую часть числа а,
а
![]() определяется по таблице 2 с помощью
равенства
определяется по таблице 2 с помощью
равенства
![]() (5)
(5)
В остальном правила сохраняются.
в случае
![]() и
и
в случае
![]() :
:
![]()
и нижняя критическая точка определяется по формуле (4), в которой
![]() (6)
(6)
В остальном правила сохраняются.
17)Закон Мальтуса.
В неограниченной стационарной и благоприятной среде размер популяции экспоненциально возрастает.
Закон Мальтуса является одним из основных экологических принципов.
Закон Мальтуса проверен экспериментально и действительно, на начальной стадии, хорошо описывает рост однородных популяций.
Показатель роста
![]() можно вычислить экспериментально по
двум измерениям.
можно вычислить экспериментально по
двум измерениям.
Пусть в момент
![]() численность популяции
численность популяции
![]() ,
,
в момент
![]() −
−
![]() .
Тогда
.
Тогда
![]()
![]()
Откуда
![]()
Логарифмируем
![]()
![]()
18)2 случай. Учет
ограниченности ресурсов. ![]() (6)
(6)
где
![]() - «ёмкость среды», т.е. максимальная
численность популяции, которую может
прокормить среда в отсутствии хищника.
- «ёмкость среды», т.е. максимальная
численность популяции, которую может
прокормить среда в отсутствии хищника.
Уравнение (2) примет вид
![]() (7)
(7)
Уравнение (7) называется логистической моделью.
Решим уравнение (7) методом разделения переменных.
![]()
![]()
Проинтегрируем
уравнение. Левая часть: 
Тогда
![]()
Откуда
![]()
![]()
С учетом начальных условий после преобразований получим
 (8)
(8)
График уравнения (8) называется логистической кривой.

Заметим, что
![]()
Уравнение (8) описывает популяцию фруктовых вредителей, некоторых видов бактерий, дрожжевых клеток:

Замечание.
До сих пор в модели процессы размножения и гибели происходят одновременно. Но в реальных популяциях интенсивность этих процессов различна в разных возрастных группах.
Если
![]() - средняя продолжительность жизни, то
получим модель
- средняя продолжительность жизни, то
получим модель
![]()
Заметим, что во всех рассматриваемых логистических моделях
![]()
при любых начальных состояниях.
