9.4. Свойства функций, непрерывных на отрезке

Функции, непрерывные на замкнутом отрезке, обладают рядом свойств, которые сформулируем в виде теорем (без доказательства).

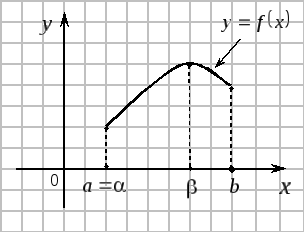
Теорема 1. Если функция непрерывна на отрезке , то она достигает на этом отрезке своего наибольшего и наименьшего значения, т.е. существуют точки и , такие, что

, . Следовательно, для всех .

На рисунке .

Следствие. Если функция непрерывна на отрезке, то она на нем органичена.

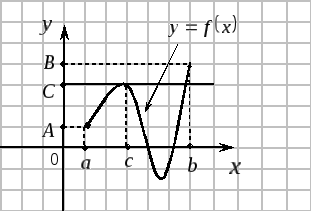
Теорема 2. Если функция непрерывна на отрезке и принимает на его концах неравные значения и , то на этом отрезке она принимает и все промежуточные значения между

и . Т.е. для любого числа , заключенного между и , найдется внутри этого отрезка такая точка , где .

Прямая пересечет график функции по крайней мере в одной точке.

С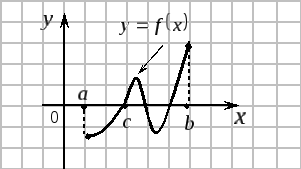ледствие. Если функция непрерывна на отрезке и на концах отрезка принимает значения разных знаков, то на этом отрезке найдется хотя бы одна точка , в которой .

Глава II. Дифференциальное исчисление

§ 10. Понятие производной, ее геометрический и физический смысл

10.1. Определение производной

Определение. Производной от функции в точке называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, т.е. .

О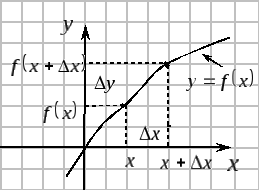бозначение: .

Используют и другие

обозначения:

, , , , .

Производная функции в точке обозначается так:

.

Функция , имеющая производную в каждой точке интервала , называется дифференцируемой на этом интервале.

Операция нахождения производной функции называется дифференцированием.

Вычислим производную функции , используя определение:

Теорема. (Связь между дифференцируемостью и непрерывностью функции).

Если функция дифференцируема в точке, то она в этой точке непрерывна. Обратное утверждение неверно.

Н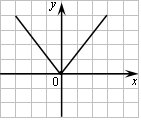апример, функция в точке непрерывна, но производная в этой точке не существует.

10.2. Геометрический смысл производной

Пусть функция определена и непрерывна на некотором интервале. Пусть точка на графике функции соответствует значению аргумента , а точка – значению , где – приращение аргумента. Проведем через точки и прямую и назовем ее секущей.

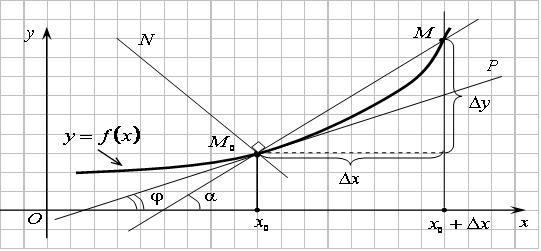
Определение. Касательной к графику функции в точке называется предельное положение секущей при неограниченном приближении точки по графику к точке (или, что то же самое, при ).

Пусть – угол между секущей и осью , – угол между касательной и осью .

На рисунке видно, что угловой коэффициент секущей равен .

Из определения касательной следует, что угловой коэффициент касательной равен

Следовательно, угловой коэффициент касательной, проведенной к графику функции в точке с абсциссой , равен значению производной функции в этой точке.

Определение. Прямая , перпендикулярная касательной и проходящая через точку касания, называется нормалью к графику функции.

– уравнение касательной,

– уравнение нормали,

где .