61. Правило добутку двох матриць.

Множення матриць

Множення двох матриць має сенс лише тоді, коли число стовпчиків першої матриці дорівнює числу рядків другої матриці. Якщо A — матриця m-на-n (m рядків, n стовпчиків), а B — матриця n-на-p (n рядків, p стовпчиків), їх добуток AB є матрицею m-на-p (m рядків, p стовпчиків), що розраховується за формулою:

(AB)[i, j] = A[i, 1] * B[1, j] + A[i, 2] * B[2, j] + ... + A[i, n] * B[n, j] для кожної пари i та j.

Наприклад,

Це множення має такі властивості:

(AB)C = A(BC) для всіх матриць A розмірності k-на-m, B розмірності m-на-n і C розмірності n-на-p (асоціативність).

(A + B)C = AC + BC для всіх матриць A і B розмірності m-на-n і матриць C розмірності n-на-k (дистрибутивність).

C(A + B) = CA + CB для всіх матриць A і B розмірності m-на-n і матриць C розмірності k-на-m (дистрибутивність).

Зауваження: комутативність має місце не завжди: для добутку певних матриць A і B може бути AB ≠ BA.

Матриці називають антикомутативними, якщо AB = −BA. Такі матриці є дуже важливими в представленнях алгебр Лі та в представленнях алгебр Кліффорда.

62. Правило добутку матриці на число.

Множення матриці A на число λ (позначення: λA) полягає в побудові матриці B, елементи якої отримані шляхом множення кожного елементу матриці A на це число, тобто кожен елемент матриці B рівний

Властивості множення матриць на число

1. 1*A = A;

2. (Λβ)A = Λ(βA)

3. (Λ+β)A = ΛA + βA

4. Λ(A+B) = ΛA + ΛB

63. Правило Крамера розв’язку слар.

спосіб розв'язання квадратних систем лінійних алгебраїчних рівнянь із ненульовим визначником основної матриці (при цьому для таких рівнянь розв'язок існує і є єдиним).

Для системи n лінійних рівнянь з n невідомими (над довільним полем)

з визначником матриці системи Δ, що не рівний нулеві, розв'язок записується у такому вигляді:

(i-й стовпчик матриці системи замінюється стовпчиком вільних членів).

Іншим чином правило Крамера формулюється так: для будь-яких коефіцієнтів c1, c2, …, cn виконується рівність:

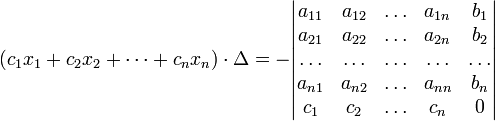
У такій формі формула Крамера справедлива без припущення, що Δ не рівне нулю, не треба навіть, аби коефіцієнти системи були елементами цілісного кільця (визначник системи навіть може бути дільником нуля у кільці коефіцієнтів). Також можна вважати, що або набори b1,b2,...,bn та x1,x2,...,xn, або набір c1,c2,...,cn складаються не з елементів кільця коефіциєнтів системи, а деякого модуля над цим кільцем. В такому вигляді формула Крамера використовується, наприклад, при доведенні формули для визначника Грама і Леми Накаями.

64. Правило суми матриць.

Складання матриць A B є операція знаходження матриці C, усі елементи якої дорівнюють попарній сумі усіх відповідних елементів матриць A і B, тобто кожен елемент матриці C рівний

Властивості складання матриць

1.комутативність;

2.асоціативність;

3.складання з нульовою матрицею;

4.існування протилежної матриці;

65. Ранг матриці. Ступінчатий вигляд матриці.

Ранг матриці — порядок найбільших відмінних від нуля мінорів цієї матриці (такі мінори називаються базисними).

У лінійній алгебрі матриця має рядкову ступінчасту форму якщо

Усі ненульові рядки (рядки, що мають хоча б один ненульовий елемент) знаходяться над нульовими рядками, і

Лідируючий коефіцієнт (перший ненульовий елемент зліва) ненульового рядка завжди строго справа від лідируючого коефіцієнта в рядку вище.

Приклад 3x3 матриці у рядковій ступінчастій формі:

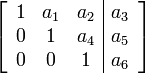
66. Рівність двох векторів.

Рівність векторів

Нехай i — два вектори площини (або простору).Кажуть, що вектор | | дорівнює вектору , і записують = , якщо:

1)довжина відрізка AB дорівнює довжині відрізка CD;

2)промені AB i CD однаково напрямлені.

67. Рівняння прямої з кутовим коефіцієнтом.

Кутовий коефіцієнт у рівнянні прямої

Якщо рівняння прямої можна записати у вигляді , то коефіцієнт k називається кутовим коефіцієнтом прямої.

1. Дві прямі паралельні тоді й тільки тоді, коли у них збігаються кутові коефіцієнти, а точки перетину з віссю ординат різні.

2. Кутовий коефіцієнт з точністю до знака дорівнює тангенсу гострого кута, утвореного прямою з віссю абсцис (або дорівнює тангенсу кута між прямою й додатним напрямком осі Ox).

3. Прямі, що задані рівняннями і, перпендикулярні тоді й тільки тоді, коли . 

68. Рівняння прямої на площині оскільки задані точки А і B належать шуканій прямій, то їх координати перетворюють рівняння прямої у істинну рівність

69. Рівняння прямої, що проходить через дві задані точки.

Нехай пряма проходить через точки і . Рівняння прямої, що проходить через точку має вигляд

(2.6)

де k — поки невідомий коефіцієнт.

Оскільки пряма проходить через точку , то координати цієї точки повинні задовольняти рівнянню (2.6): .Звідси знаходимо . Підставляючи знайдене значення k в рівняння (2.6), отримаємо рівняння прямої, що проходить через точки М₁ і М₂:

(2.7)

Передбачається, що в цьому рівнянні .

Якщо x₂=x₁, то пряма, що проходить через точки і , паралельна осі ординат. Її рівняння має вид х = х₁.

Якщо у₂ = у₁, то рівняння прямої може бути записане у вигляді у = у₁, пряма М₁М₂ паралельна осі абсцис.